The tensor product is a fundamental operation in linear algebra that combines two vector spaces into a new, higher-dimensional space, capturing interactions between elements of the original spaces. It plays a crucial role in quantum mechanics, computer science, and multilinear algebra by enabling complex transformations and representations. Explore the article to understand how the tensor product can enhance your comprehension of advanced mathematical structures and applications.
Table of Comparison
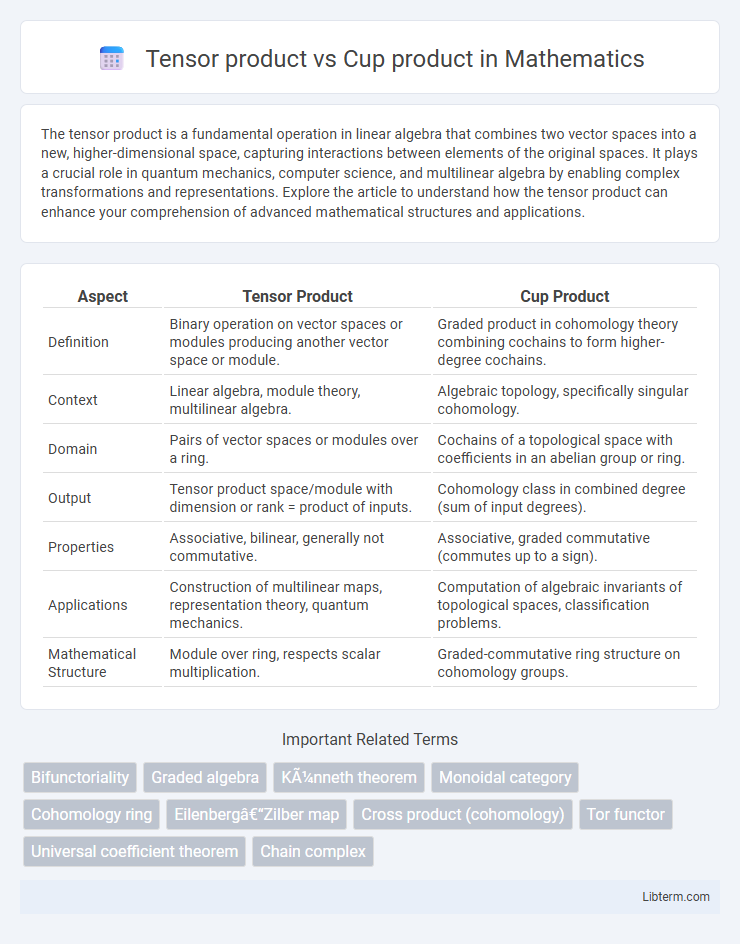
| Aspect | Tensor Product | Cup Product |
|---|---|---|
| Definition | Binary operation on vector spaces or modules producing another vector space or module. | Graded product in cohomology theory combining cochains to form higher-degree cochains. |
| Context | Linear algebra, module theory, multilinear algebra. | Algebraic topology, specifically singular cohomology. |
| Domain | Pairs of vector spaces or modules over a ring. | Cochains of a topological space with coefficients in an abelian group or ring. |
| Output | Tensor product space/module with dimension or rank = product of inputs. | Cohomology class in combined degree (sum of input degrees). |
| Properties | Associative, bilinear, generally not commutative. | Associative, graded commutative (commutes up to a sign). |
| Applications | Construction of multilinear maps, representation theory, quantum mechanics. | Computation of algebraic invariants of topological spaces, classification problems. |
| Mathematical Structure | Module over ring, respects scalar multiplication. | Graded-commutative ring structure on cohomology groups. |
Introduction to Tensor Product and Cup Product
Tensor product in algebra combines two modules or vector spaces into a new one, capturing bilinear relationships by pairing elements from each space to form ordered pairs that satisfy linearity properties. Cup product, used in algebraic topology and cohomology theory, is an operation on cochain complexes that produces a graded ring structure by combining cohomology classes, reflecting the intersection properties of topological spaces. Both operations are fundamental in their respective fields, with the tensor product emphasizing algebraic constructions and the cup product encoding topological interaction between cohomology classes.
Historical Development and Origins
The concepts of tensor product and cup product emerged from distinct areas of mathematical research in the early 20th century. The tensor product was formalized by mathematicians such as Giuseppe Peano and Emmy Noether to generalize multilinear algebra, providing a foundational tool for vector spaces and modules. The cup product originated in algebraic topology, introduced by J. W. Alexander and further developed by Samuel Eilenberg and Norman Steenrod in the 1940s to define products in cohomology rings, linking topological spaces and algebraic invariants.
Fundamental Definitions and Concepts
The tensor product combines two vector spaces or modules into a new space representing all bilinear maps, critical in multilinear algebra and category theory. The cup product, a cohomological operation in algebraic topology, combines cochains to form higher-degree cohomology classes, encoding intersection data on topological spaces. Tensor products focus on algebraic structure construction, while cup products reveal topological invariants through cohomology ring multiplications.
Algebraic Structures Involved
Tensor products involve bilinear maps between modules or vector spaces, creating a new module that encodes interactions between the original structures in a linear fashion. Cup products arise in cohomology rings, combining cochains to endow cohomology groups with a graded-commutative ring structure using algebraic topology tools. The tensor product typically operates within module categories over a ring, while the cup product functions in cochain complexes, reflecting topological and algebraic structures through homological algebra.
Tensor Product: Applications and Examples
The tensor product is a fundamental operation in linear algebra and multilinear algebra used to construct higher-dimensional spaces from given vector spaces, widely applied in quantum computing for combining state spaces and in differential geometry for building tensor fields. It enables the representation of multilinear maps as linear maps, facilitating computations in physics, engineering, and computer science, such as in the formulation of spacetime tensors in general relativity. Examples include the tensor product of matrices to form block matrices and the tensor product of vector spaces in the study of entangled states in quantum mechanics.
Cup Product: Applications and Examples
The cup product is a fundamental operation in cohomology theories, particularly singular cohomology, where it provides a graded ring structure that encodes topological information about spaces. It has crucial applications in algebraic topology, including the characterization of manifold structures, calculation of intersection numbers, and distinguishing non-homeomorphic spaces. Examples include the cup product in the cohomology ring of real projective spaces, which reveals essential information about their geometric and algebraic properties.
Comparative Analysis: Similarities and Differences
Tensor product and cup product both serve to combine algebraic objects, but they operate in distinct contexts with different structural properties. The tensor product produces an object in a product category, such as modules or vector spaces, preserving bilinearity and enabling multilinear operations, while the cup product specifically acts in cohomology, taking cochains and producing a new cohomology class, encoding topological information. Unlike the tensor product, which is a purely algebraic construction expanding the space, the cup product integrates algebraic and topological features by leveraging the cochain complex and its graded ring structure.
Role in Homology and Cohomology Theories
The tensor product plays a crucial role in homology theories by combining chain complexes to form new complexes whose homology provides insights into product spaces. The cup product is essential in cohomology theories, defining a graded ring structure on cohomology groups that encodes intersection and interaction of cohomological classes. Both constructions reveal algebraic structures reflecting topological properties, with the tensor product focusing on homological operations and the cup product capturing multiplicative cohomological information.
Computational Methods and Techniques
Tensor product and cup product represent distinct algebraic operations crucial in computational topology and homological algebra. Tensor products combine chain complexes or modules, facilitating calculations in multilinear algebra, while cup products operate on cohomology classes, providing a graded ring structure essential for computations in algebraic topology. Efficient algorithms for tensor products focus on matrix representations and Kronecker products, whereas cup product computations often employ simplicial or cellular cochains with boundary maps, highlighting different computational techniques adapted to their algebraic contexts.
Conclusion: Choosing the Right Product
Selecting between the tensor product and the cup product depends on the mathematical context and desired outcome; tensor products combine vector spaces or modules, preserving linear structures, while cup products operate in cohomology to define algebraic invariants. Tensor products are crucial in multilinear algebra and representation theory, facilitating the construction of complex objects from simpler ones. Cup products provide a graded ring structure essential in algebraic topology, enabling the study of topological spaces through cohomological interactions.
Tensor product Infographic
 libterm.com
libterm.com