The Weierstrass Approximation Theorem states that every continuous function defined on a closed interval can be uniformly approximated as closely as desired by polynomial functions. This foundational result in analysis ensures that polynomials serve as powerful tools for modeling and approximation in various applications. Explore the rest of the article to understand the theorem's implications and practical uses for your mathematical endeavors.
Table of Comparison
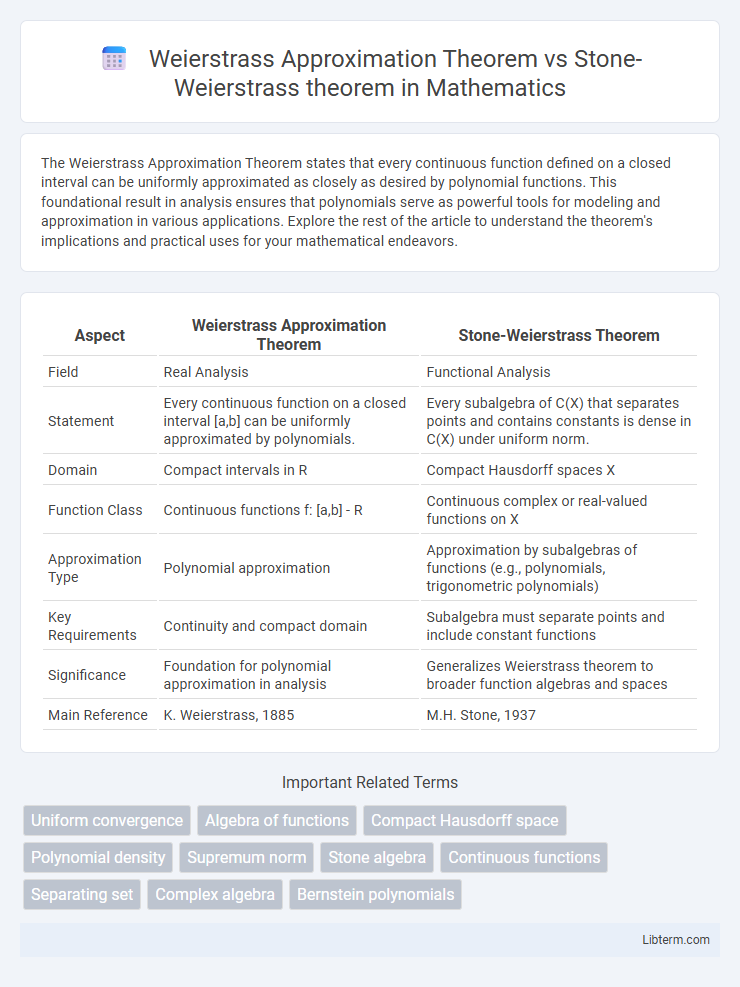
| Aspect | Weierstrass Approximation Theorem | Stone-Weierstrass Theorem |
|---|---|---|
| Field | Real Analysis | Functional Analysis |
| Statement | Every continuous function on a closed interval [a,b] can be uniformly approximated by polynomials. | Every subalgebra of C(X) that separates points and contains constants is dense in C(X) under uniform norm. |
| Domain | Compact intervals in R | Compact Hausdorff spaces X |
| Function Class | Continuous functions f: [a,b] - R | Continuous complex or real-valued functions on X |
| Approximation Type | Polynomial approximation | Approximation by subalgebras of functions (e.g., polynomials, trigonometric polynomials) |
| Key Requirements | Continuity and compact domain | Subalgebra must separate points and include constant functions |
| Significance | Foundation for polynomial approximation in analysis | Generalizes Weierstrass theorem to broader function algebras and spaces |
| Main Reference | K. Weierstrass, 1885 | M.H. Stone, 1937 |
Introduction to Function Approximation in Analysis
The Weierstrass Approximation Theorem establishes that any continuous function defined on a closed interval can be uniformly approximated by polynomials, providing a fundamental tool in function approximation within real analysis. The Stone-Weierstrass theorem extends this concept by allowing approximation using subalgebras of continuous functions on compact Hausdorff spaces, significantly broadening the scope beyond polynomials. Both theorems are central to approximation theory, enabling the representation of complex functions by simpler, well-understood functions for analysis and computation.
Understanding the Weierstrass Approximation Theorem
The Weierstrass Approximation Theorem states that any continuous real-valued function defined on a closed interval [a, b] can be uniformly approximated by polynomial functions, highlighting the foundational role of polynomials in function approximation. This theorem ensures the density of polynomial functions in the space of continuous functions equipped with the uniform norm, facilitating practical applications in numerical analysis and approximation theory. Unlike the Stone-Weierstrass theorem, which generalizes this concept to algebras of functions on compact spaces, the Weierstrass theorem specifically addresses approximation by polynomials on real intervals.
Historical Context and Significance of Weierstrass Theorem
Weierstrass Approximation Theorem, established by Karl Weierstrass in 1885, laid the foundation for approximation theory by proving that every continuous real-valued function on a closed interval can be uniformly approximated by polynomials, marking a breakthrough in analysis. This classical result demonstrated the power of polynomials in function approximation, influencing subsequent developments in functional analysis. The Stone-Weierstrass theorem, formulated later by Marshall Stone in 1937, generalized Weierstrass's theorem to algebras of functions on compact spaces, extending its applicability beyond real intervals and cementing its central role in modern mathematical analysis.
Limitations of the Classical Weierstrass Theorem
The classical Weierstrass Approximation Theorem guarantees uniform approximation of continuous real-valued functions on a closed interval by polynomials, but it is limited to one-dimensional domains and lacks applicability to more complex spaces or functions defined on general compact Hausdorff spaces. The Stone-Weierstrass Theorem generalizes this result by allowing uniform approximation using subalgebras of continuous functions, thus extending to multivariate and abstract function spaces while overcoming the dimensional and topological restrictions of the classical theorem. These advancements enable approximation in broader contexts, such as algebras of continuous functions on compact metric spaces, highlighting the classical theorem's constraints in multivariate and non-polynomial approximation scenarios.
Introduction to the Stone-Weierstrass Theorem
The Stone-Weierstrass Theorem generalizes the Weierstrass Approximation Theorem by extending uniform approximation from continuous functions on closed intervals to more general compact Hausdorff spaces using subalgebras of C(X). It states that any subalgebra of continuous functions that separates points and contains the constant functions is dense in C(X) with respect to the uniform norm. This powerful result underpins functional analysis and approximation theory by enabling the approximation of complex function spaces beyond polynomial functions on real intervals.
Generalization from Weierstrass to Stone-Weierstrass
The Weierstrass Approximation Theorem asserts that any continuous real-valued function defined on a closed interval can be uniformly approximated by polynomial functions. The Stone-Weierstrass theorem extends this result by generalizing polynomial approximations to more abstract algebras of functions on compact Hausdorff spaces, allowing uniform approximation by subalgebras that separate points and contain constants. This generalization enables the approximation of a wider class of continuous functions beyond intervals, covering multidimensional and complex spaces with greater algebraic flexibility.
Key Differences Between Both Theorems
The Weierstrass Approximation Theorem states that any continuous real-valued function defined on a closed interval can be uniformly approximated by polynomial functions, emphasizing approximation within compact intervals in \(\mathbb{R}\). The Stone-Weierstrass theorem generalizes this result by applying to algebras of continuous functions on compact Hausdorff spaces, extending beyond polynomials to more general function classes and topological settings. Key differences include the scope of spaces considered--intervals versus compact Hausdorff spaces--and the algebraic structures used for approximation, with Weierstrass focusing on polynomials and Stone-Weierstrass on subalgebras that separate points and contain constants.
Applications in Modern Mathematical Analysis
The Weierstrass Approximation Theorem guarantees that any continuous function defined on a closed interval can be uniformly approximated by polynomial functions, which is fundamental in numerical analysis and computational methods. The Stone-Weierstrass Theorem extends this concept by allowing uniform approximation on compact Hausdorff spaces using subalgebras of continuous functions, playing a crucial role in functional analysis and the theory of C*-algebras. These theorems underpin techniques in approximation theory, spectral theory, and the modern study of Banach spaces, enabling precise modeling in engineering, physics, and data science.
Examples Illustrating Both Theorems
The Weierstrass Approximation Theorem states that any continuous function defined on a closed interval [a, b] can be uniformly approximated by polynomials, exemplified by approximating f(x) = |x| on [-1, 1] using Bernstein polynomials. The Stone-Weierstrass Theorem generalizes this result to algebras of functions on compact Hausdorff spaces, allowing approximation by subalgebras such as trigonometric polynomials approximating continuous periodic functions on the unit circle. For instance, the algebra of complex exponentials e^{inx} densely approximates any continuous function on the circle, demonstrating Stone-Weierstrass's broader applicability beyond real intervals.
Conclusion: Impact on Functional Approximation Theory
The Weierstrass Approximation Theorem establishes that any continuous real-valued function on a closed interval can be uniformly approximated by polynomial functions, laying the foundation for classical functional approximation theory. The Stone-Weierstrass Theorem generalizes this result to broader spaces by asserting that any subalgebra of continuous functions that separates points and contains the constants is dense in the space of continuous functions, significantly expanding applications in functional analysis and approximation. These theorems together underpin modern approximation techniques, enabling robust methods in numerical analysis, engineering, and applied sciences.
Weierstrass Approximation Theorem Infographic
 libterm.com
libterm.com