The fundamental group is a key concept in algebraic topology that captures the notion of loop structures within a topological space, providing insight into its shape and connectivity. It assigns a group to a space by considering equivalence classes of loops based on continuous deformation, helping classify spaces based on their topological properties. Explore the rest of this article to understand how the fundamental group influences various fields and applications in mathematics.
Table of Comparison
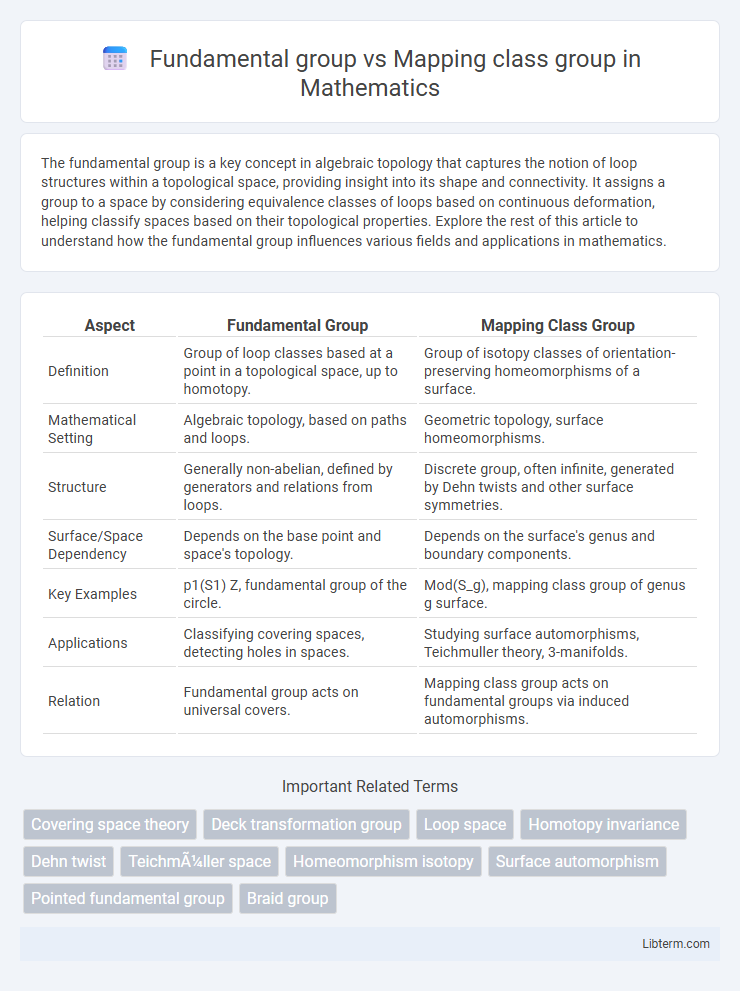
| Aspect | Fundamental Group | Mapping Class Group |
|---|---|---|
| Definition | Group of loop classes based at a point in a topological space, up to homotopy. | Group of isotopy classes of orientation-preserving homeomorphisms of a surface. |
| Mathematical Setting | Algebraic topology, based on paths and loops. | Geometric topology, surface homeomorphisms. |
| Structure | Generally non-abelian, defined by generators and relations from loops. | Discrete group, often infinite, generated by Dehn twists and other surface symmetries. |
| Surface/Space Dependency | Depends on the base point and space's topology. | Depends on the surface's genus and boundary components. |
| Key Examples | p1(S1) Z, fundamental group of the circle. | Mod(S_g), mapping class group of genus g surface. |
| Applications | Classifying covering spaces, detecting holes in spaces. | Studying surface automorphisms, Teichmuller theory, 3-manifolds. |
| Relation | Fundamental group acts on universal covers. | Mapping class group acts on fundamental groups via induced automorphisms. |
Introduction to Fundamental Group and Mapping Class Group
The fundamental group, denoted p1(X, x0), captures the topological essence of a space X by classifying loops based at a point x0 up to homotopy, revealing information about the space's path-connectedness and holes. The mapping class group, typically defined for a surface S, consists of orientation-preserving homeomorphisms of S modulo isotopy, encoding symmetries and deformation classes of the surface. Both groups serve as central tools in algebraic topology and geometric group theory, linking surface topology with algebraic structures.
Definitions: Fundamental Group Explained
The fundamental group, denoted p1(X, x0), is the group of loops based at a point x0 in a topological space X, with loops considered up to continuous deformation (homotopy). It encodes essential information about the space's shape, detecting holes and obstacles by classifying possible loop paths. In contrast, the mapping class group consists of isotopy classes of homeomorphisms of a surface, capturing symmetries and self-equivalences rather than loop-based homotopy information.
Definitions: Mapping Class Group Explained
The fundamental group captures the loops based at a fixed point in a topological space, revealing its basic shape by classifying paths up to homotopy. The mapping class group consists of isotopy classes of orientation-preserving homeomorphisms of a surface, encoding symmetries and deformations of the surface beyond continuous loops. Understanding the mapping class group is crucial in geometric topology and Teichmuller theory, as it generalizes surface automorphisms and governs moduli spaces of Riemann surfaces.
Algebraic Structure: Comparing the Two Groups
The fundamental group, p1(X), encodes loops based at a point in a topological space X and is a primary invariant in algebraic topology, featuring a well-defined group structure through concatenation of loops. The mapping class group, Mod(S), arises from isotopy classes of orientation-preserving homeomorphisms of a surface S and captures global symmetries of the surface, exhibiting a richer, often nonabelian structure. While p1(X) reflects the local path-connectedness properties, Mod(S) governs the global deformation types, presenting a complex interplay between topology and group theory in low-dimensional manifolds.
Topological Significance of Fundamental Group
The fundamental group captures essential information about the loops in a topological space, classifying paths based on continuous deformation and revealing the space's intrinsic connectivity properties. It serves as a primary algebraic invariant that distinguishes spaces with different hole structures or handles, playing a crucial role in algebraic topology. In contrast, the mapping class group encodes symmetries of surfaces via isotopy classes of homeomorphisms, making the fundamental group foundational for understanding these higher-level symmetries and their actions on surface topology.
Geometric Role of Mapping Class Group
The mapping class group acts as the group of isotopy classes of orientation-preserving homeomorphisms of a surface, encoding its geometric symmetries and moduli space structure. Unlike the fundamental group, which captures loops and paths based on homotopy classes, the mapping class group governs global surface deformations preserving topological type, critically influencing Teichmuller theory and low-dimensional topology. Its action on the surface's universal cover and on curve complexes offers profound insights into surface automorphisms and geometric group theory.
Relationship and Connections between the Groups
The fundamental group encodes the topological loops of a space up to homotopy, serving as a key invariant in algebraic topology, while the mapping class group consists of isotopy classes of orientation-preserving homeomorphisms of a surface. The mapping class group acts naturally on the fundamental group by automorphisms, establishing a profound relationship that connects surface topology to group actions and symmetries. This interplay is pivotal in understanding moduli spaces, Teichmuller theory, and the algebraic structure of surface homeomorphisms.
Examples from Surfaces and Manifolds
The fundamental group captures loops on surfaces such as the torus, where p1(T2) Z2, reflecting how loops wind around the two principal directions. The mapping class group of a closed surface S_g of genus g, generated by Dehn twists, acts on p1(S_g) by outer automorphisms, highlighting the deep interplay between surface homeomorphisms and loop classes. In higher-dimensional manifolds, the fundamental group remains crucial for classifying covering spaces, while mapping class groups--less understood--often connect to diffeomorphism groups and moduli spaces, exemplified by 3-manifolds where Heegaard splittings induce mapping class group actions on surface groups.
Applications in Mathematics and Physics
The fundamental group encodes the topological structure of spaces, playing a crucial role in algebraic topology, while the mapping class group captures the symmetries of surfaces through isotopy classes of homeomorphisms, essential in low-dimensional topology and geometric group theory. In mathematics, the fundamental group aids in classifying covering spaces and detecting topological invariants, whereas the mapping class group informs the study of moduli spaces of Riemann surfaces and Teichmuller theory. In physics, these groups underpin the analysis of topological quantum field theories, with fundamental groups influencing particle statistics and mapping class groups governing monodromy in conformal field theory and string theory.
Key Differences and Summary
The fundamental group captures the algebraic structure of loops based at a point in a topological space, reflecting its basic shape and connectivity, while the mapping class group consists of isotopy classes of homeomorphisms of a surface, encoding symmetries and deformations of that surface. The fundamental group is a group defined purely from paths and loops, often non-abelian for complex spaces, whereas the mapping class group incorporates geometric transformations, capturing more global surface properties. In summary, the fundamental group studies local loop structures, and the mapping class group classifies global surface automorphisms, making their roles complementary in topology.
Fundamental group Infographic
 libterm.com
libterm.com