The Frobenius norm measures the size of a matrix by calculating the square root of the sum of the absolute squares of its elements, providing a straightforward way to assess matrix magnitude. It is widely used in numerical analysis, machine learning, and signal processing for error estimation and optimization tasks. Explore the rest of the article to understand how your applications can benefit from the Frobenius norm's properties.
Table of Comparison
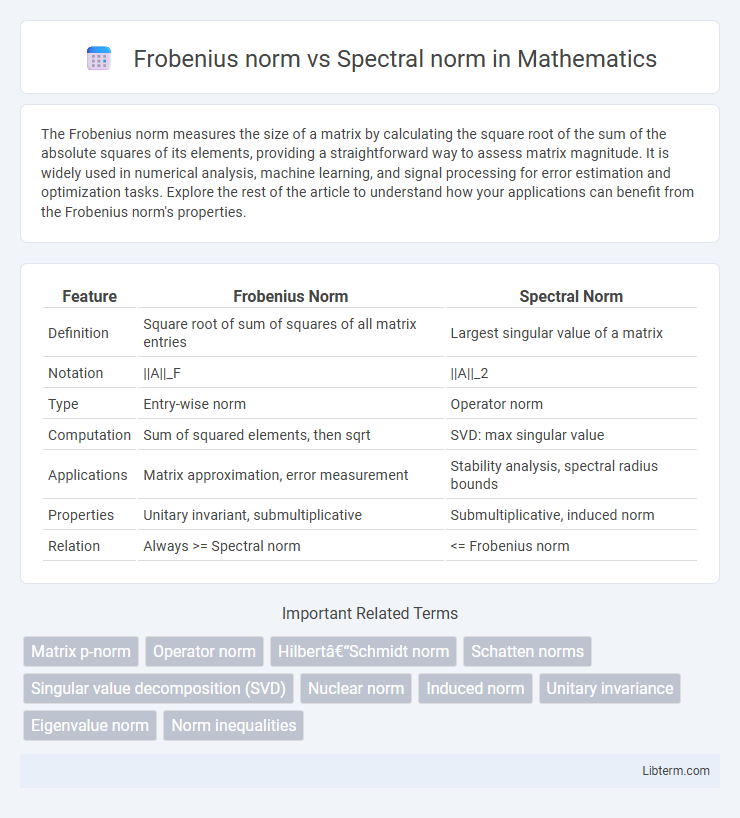
| Feature | Frobenius Norm | Spectral Norm |
|---|---|---|
| Definition | Square root of sum of squares of all matrix entries | Largest singular value of a matrix |
| Notation | ||A||_F | ||A||_2 |
| Type | Entry-wise norm | Operator norm |
| Computation | Sum of squared elements, then sqrt | SVD: max singular value |
| Applications | Matrix approximation, error measurement | Stability analysis, spectral radius bounds |
| Properties | Unitary invariant, submultiplicative | Submultiplicative, induced norm |
| Relation | Always >= Spectral norm | <= Frobenius norm |
Introduction to Matrix Norms
Matrix norms quantify the size or length of matrices and are fundamental in numerical analysis and linear algebra. The Frobenius norm measures a matrix's magnitude by computing the square root of the sum of the absolute squares of its elements, reflecting the Euclidean norm of the matrix viewed as a vector. The spectral norm, equal to the largest singular value of the matrix, captures the maximum stretching factor applied by the matrix when acting on a vector, thereby indicating its operator norm induced by the Euclidean vector norm.
Definition of Frobenius Norm
The Frobenius norm of a matrix is defined as the square root of the sum of the absolute squares of its elements, providing a measure of the matrix's overall magnitude. It is calculated by taking the square root of the trace of the matrix multiplied by its conjugate transpose, making it analogous to the Euclidean norm for vectors. Unlike the spectral norm, which measures the largest singular value, the Frobenius norm captures the combined energy of all singular values in the matrix.
Definition of Spectral Norm
The spectral norm of a matrix, also known as the operator 2-norm, is defined as the largest singular value of the matrix, representing the maximum stretching factor the matrix applies to any vector. It is calculated as the square root of the largest eigenvalue of the matrix multiplied by its conjugate transpose. In contrast, the Frobenius norm is defined as the square root of the sum of the absolute squares of all the matrix entries, measuring the overall magnitude of the matrix elements.
Mathematical Formulation and Notation
The Frobenius norm of a matrix \( A \in \mathbb{R}^{m \times n} \) is defined as \( \|A\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2} \), representing the square root of the sum of the absolute squares of its elements. The spectral norm, denoted \( \|A\|_2 \), is the largest singular value of \( A \), formally expressed as \( \|A\|_2 = \sigma_{\max}(A) = \max_{\|x\|_2=1} \|Ax\|_2 \). While the Frobenius norm can be seen as the Euclidean norm of the matrix viewed as a vector, the spectral norm quantifies the maximum stretching effect of \( A \) on any unit vector in the domain.
Key Differences Between Frobenius and Spectral Norms
The Frobenius norm measures the square root of the sum of the absolute squares of all matrix elements, reflecting the overall energy content of the matrix, while the spectral norm equals the largest singular value, indicating the maximum stretching factor of the matrix. Frobenius norm is always greater than or equal to the spectral norm and is computationally simpler, making it suitable for applications requiring a measure of total magnitude. Spectral norm provides a tighter bound for operator-induced effects, commonly used in stability analysis and control theory where the matrix's action on vectors is critical.
Computational Complexity and Efficiency
The Frobenius norm requires O(mn) operations for an m-by-n matrix, as it sums the squares of all entries, making it computationally efficient for large-scale problems. The spectral norm, defined as the largest singular value, demands SVD or power iteration methods, typically involving O(mn^2) complexity for dense matrices, thus being more computationally intensive. Therefore, the Frobenius norm is preferred in scenarios where efficiency is critical, while the spectral norm is used when the matrix's dominant singular value is essential for analysis.
Geometric Interpretations
The Frobenius norm of a matrix represents the square root of the sum of the squares of all its elements, reflecting the Euclidean length of the matrix regarded as a vector in a high-dimensional space. The spectral norm corresponds to the largest singular value of the matrix, indicating the maximum amount by which the matrix can stretch a unit vector, thus capturing the matrix's dominant geometric distortion. Geometrically, the Frobenius norm measures overall matrix size while the spectral norm quantifies the greatest directional scaling effect.
Use Cases and Applications
The Frobenius norm is widely used in applications requiring element-wise error measurement and matrix approximation, such as in machine learning for regularization and low-rank matrix factorization. The spectral norm, representing the largest singular value, is crucial in stability analysis of systems and control theory, where it measures the maximum amplification of a signal by a matrix. Both norms play integral roles in numerical linear algebra, but Frobenius norm excels in comprehensive error metrics, while spectral norm is preferred for bounding operator behavior.
Advantages and Limitations
The Frobenius norm offers computational efficiency and simplicity by summing the squares of all matrix elements, making it advantageous for tasks requiring element-wise error measurement and gradient calculations. Its limitation lies in sensitivity to matrix size, which can obscure information about the dominant singular values and spectral properties. The Spectral norm, representing the largest singular value, excels in capturing the maximum matrix amplification effect and stability analysis but involves higher computational cost and complexity, restricting its use in large-scale or element-wise error contexts.
Summary and Conclusion
The Frobenius norm measures the overall magnitude of a matrix by summing the squares of all its elements, reflecting the Euclidean norm of its entries. The spectral norm, equal to the largest singular value, indicates the maximum stretching factor of the matrix as a linear operator. While the Frobenius norm is easier to compute and useful for element-wise analysis, the spectral norm provides critical insights into operator behavior and stability in applications like numerical analysis and machine learning.
Frobenius norm Infographic
 libterm.com
libterm.com