A simply connected space is a fundamental concept in topology, describing a shape without holes where every loop can be continuously contracted to a single point. This property is crucial in fields like complex analysis and algebraic topology, influencing how functions behave on these spaces. Explore the rest of the article to understand how simply connected spaces impact various mathematical and physical theories.
Table of Comparison
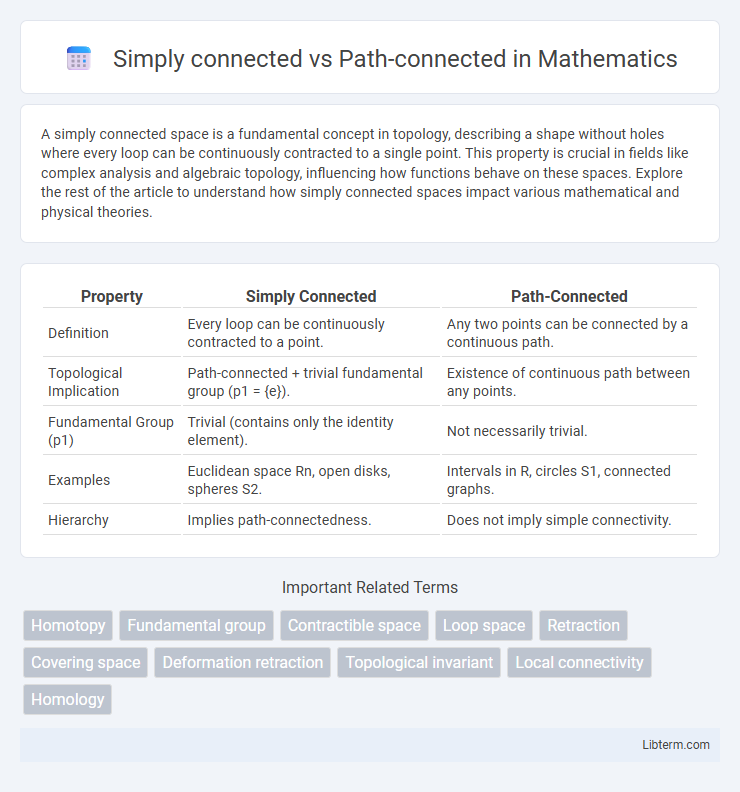
| Property | Simply Connected | Path-Connected |
|---|---|---|
| Definition | Every loop can be continuously contracted to a point. | Any two points can be connected by a continuous path. |
| Topological Implication | Path-connected + trivial fundamental group (p1 = {e}). | Existence of continuous path between any points. |
| Fundamental Group (p1) | Trivial (contains only the identity element). | Not necessarily trivial. |
| Examples | Euclidean space Rn, open disks, spheres S2. | Intervals in R, circles S1, connected graphs. |
| Hierarchy | Implies path-connectedness. | Does not imply simple connectivity. |
Introduction to Topological Connectivity
Simply connected spaces are those where every loop can be continuously contracted to a point, indicating no holes or obstructions in the topology. Path-connected spaces allow any two points to be joined by a continuous path, ensuring overall spatial coherence but not necessarily trivial loop contraction. The distinction is fundamental in algebraic topology, with simply connected implying path-connected, but not vice versa, highlighting different levels of topological connectivity.
Defining Simply Connected Spaces
Simply connected spaces are topological spaces that are path-connected and have trivial fundamental groups, meaning every loop can be continuously contracted to a single point within the space. Path-connectedness ensures any two points can be joined by a continuous path, but does not guarantee the absence of holes or obstacles that prevent loop contraction. Defining simply connected spaces requires both path-connectedness and the absence of non-contractible loops, essential in fields like algebraic topology and complex analysis.
Understanding Path-Connected Spaces
Path-connected spaces allow any two points to be joined by a continuous path within the space, ensuring a flexible notion of connectedness that supports continuous deformation. Simply connected spaces extend this concept by requiring every loop within the space to be continuously contracted to a single point, implying no holes or obstructions in higher dimensions. Understanding path-connectedness is fundamental for exploring complex topological properties, as it guarantees the existence of paths but does not address the space's loop structure or higher homotopy features.
Key Differences Between Simply Connected and Path-Connected
Simply connected spaces have no holes, meaning every loop can be continuously contracted to a point, whereas path-connected spaces only require any two points to be joined by a continuous path. Simply connected implies path-connected, but path-connected does not imply simply connected, as spaces like a circle are path-connected but not simply connected. The key difference lies in the presence of non-contractible loops, which are prohibited in simply connected spaces but allowed in path-connected spaces.
Examples of Simply Connected Spaces
Examples of simply connected spaces include the Euclidean plane \(\mathbb{R}^2\) and higher-dimensional Euclidean spaces \(\mathbb{R}^n\) for \(n \geq 2\), where every loop can be continuously contracted to a point without leaving the space. The 2-dimensional sphere \(S^2\) is simply connected because any loop on the sphere can shrink to a point without obstruction. In contrast, the punctured plane \(\mathbb{R}^2 \setminus \{0\}\) is path-connected but not simply connected, demonstrating the key difference between these topological properties.
Examples of Path-Connected but Not Simply Connected Spaces
The classic example of a path-connected but not simply connected space is the punctured plane \(\mathbb{R}^2 \setminus \{0\}\), which allows continuous paths between any two points but contains a loop that cannot be continuously contracted to a point without leaving the space. Another instance is the torus \(T^2\), where any two points can be joined by a path, yet loops around the holes are non-contractible, demonstrating non-simple connectivity. These spaces highlight the difference between path connectivity, ensuring connectedness by paths, and simple connectivity, requiring all loops to be contractible within the space.
Importance in Topology and Mathematics
Simply connected spaces play a crucial role in topology as they ensure the absence of holes, enabling any loop to be continuously contracted to a point, which is vital for complex analysis and algebraic topology. Path-connectedness guarantees that any two points within a space can be joined by a continuous path, ensuring the space's cohesion and fundamental connectivity properties. Understanding the distinction between simply connected and path-connected spaces is essential in fields like homotopy theory and manifold theory, where the shape and connectivity influence the behavior of functions and spaces.
Common Misconceptions and Clarifications
Simply connected spaces are often misunderstood as being the same as path-connected spaces, but a simply connected space must not only be path-connected but also have a trivial fundamental group, meaning any loop can be continuously contracted to a point. Path-connectedness only requires that any two points can be joined by a path, without constraints on the nature of loops within the space. Clarifying this distinction helps avoid misconceptions in topology, where simply connectedness implies a stronger condition than path-connectedness alone.
Real-World Applications of Connectivity Concepts
Simply connected spaces, characterized by having no holes and every loop contractible to a point, are critical in robotics for ensuring obstacle-free navigation and path planning in real-world environments. Path-connectedness guarantees that any two points in a space can be connected by a continuous path, which underpins network routing and communication protocols in wireless sensor networks and urban traffic systems. Understanding these connectivity concepts optimizes design in engineering, enabling reliable robot motion and efficient data transmission in complex systems.
Conclusion: Choosing the Right Concept
Choosing between simply connected and path-connected spaces depends on the topological properties relevant to your application; simply connected spaces guarantee no holes and unique loop contraction, crucial for complex analysis and algebraic topology. Path-connected spaces ensure any two points can be joined by a continuous path, essential for continuity and connectivity in geometric contexts. Understanding these distinctions helps select the appropriate concept for rigorous mathematical modeling and problem-solving.
Simply connected Infographic
 libterm.com
libterm.com