A closed set in topology is a set that contains all its limit points, making it complementary to an open set within a given space. It plays a crucial role in defining continuity, convergence, and boundary behavior of functions. Explore the rest of the article to understand how closed sets influence various mathematical concepts and their applications.
Table of Comparison
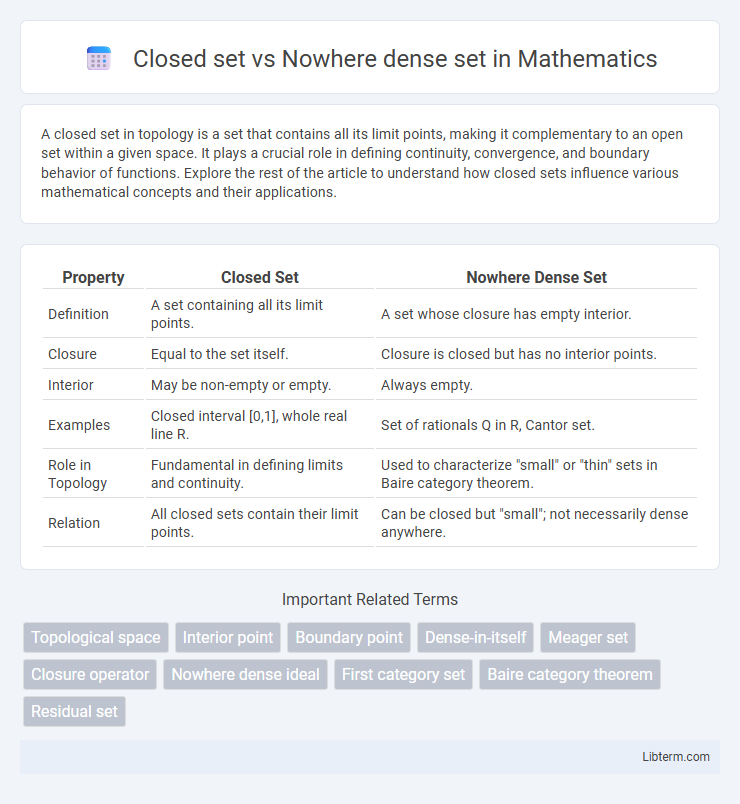
| Property | Closed Set | Nowhere Dense Set |
|---|---|---|
| Definition | A set containing all its limit points. | A set whose closure has empty interior. |
| Closure | Equal to the set itself. | Closure is closed but has no interior points. |
| Interior | May be non-empty or empty. | Always empty. |
| Examples | Closed interval [0,1], whole real line R. | Set of rationals Q in R, Cantor set. |
| Role in Topology | Fundamental in defining limits and continuity. | Used to characterize "small" or "thin" sets in Baire category theorem. |
| Relation | All closed sets contain their limit points. | Can be closed but "small"; not necessarily dense anywhere. |
Introduction to Closed Sets and Nowhere Dense Sets
Closed sets are defined as sets that contain all their limit points, ensuring the inclusion of boundary elements within the set, which makes them fundamental in topology and real analysis. Nowhere dense sets are subsets whose closures have empty interiors, meaning they are "small" or sparse in a topological space and do not contain any open sets. Understanding the properties of closed sets and nowhere dense sets is crucial for studying the structure and distribution of sets within metric and topological spaces.
Basic Definitions and Concepts
A closed set in topology is defined as a set that contains all its limit points, meaning it includes its boundary and complements an open set. A nowhere dense set is characterized by having an empty interior closure, indicating it is "thin" or sparse within the space and does not contain any open subset. Understanding the distinction involves recognizing that closed sets can have non-empty interiors, while nowhere dense sets have closures with no interior points, reflecting their minimal topological influence.
Properties of Closed Sets
Closed sets contain all their limit points, ensuring any convergent sequence within the set converges to a point also inside it, which supports completeness in metric spaces. They are stable under arbitrary intersections and finite unions, making them fundamental in defining topological closures. Unlike nowhere dense sets that have empty interiors and do not contain open subsets, closed sets can contain intervals or entire neighborhoods, highlighting their robustness in topological structure.
Properties of Nowhere Dense Sets
Nowhere dense sets in a topological space have an empty interior, meaning no open set lies entirely within them, contrasting with closed sets that contain all their limit points. These sets remain "small" in terms of category, as their closure has no nonempty open subsets, illustrating their sparsity compared to closed sets which can be large and dense. In metric spaces, nowhere dense sets play a crucial role in the Baire category theorem, emphasizing their negligible size and influence on the structure of the space.
Key Differences Between Closed Sets and Nowhere Dense Sets
Closed sets contain all their limit points and are equal to their closure, ensuring completeness within a topological space, while nowhere dense sets have closures with empty interiors, meaning they are "small" and do not densely occupy any region. In metric spaces, closed sets can be large or contain entire intervals, whereas nowhere dense sets are sparse, failing to include any open subset. The key difference lies in density properties: closed sets may be large and "thick," whereas nowhere dense sets are fundamentally "thin" or negligible in terms of interior points.
Examples of Closed Sets
Closed sets include fundamental examples such as the interval [0, 1] on the real number line, which contains all its limit points, and the set of all integers \(\mathbb{Z}\), which is closed under the standard topology on \(\mathbb{R}\). Another instance is the unit circle \(S^1 = \{(x,y) \in \mathbb{R}^2 : x^2 + y^2 = 1\}\), a closed set in \(\mathbb{R}^2\) that also highlights closure properties in higher dimensions. In contrast, nowhere dense sets, like the Cantor set, have closures with empty interior, distinguishing them from typical closed sets that possess non-empty interiors or full closures.
Examples of Nowhere Dense Sets
A nowhere dense set in a topological space is a set whose closure has an empty interior, making it "small" in terms of topological size. Classic examples include the Cantor set in the real line, which is closed, nowhere dense, and uncountable, and the set of integers within the real numbers, which is closed yet nowhere dense because it lacks any intervals. In contrast, a closed set may have nonempty interior, such as closed intervals like [0,1] in the real numbers, distinguishing it from nowhere dense sets that cannot contain open subsets.
Topological Significance and Applications
Closed sets in topology contain all their limit points, making them essential for defining continuity, convergence, and compactness in various spaces. Nowhere dense sets, characterized by having empty interior in their closure, play a crucial role in measure theory and Baire category theorem, often used to identify "small" or "thin" sets within topological spaces. Their distinct properties allow researchers to analyze dense and sparse regions in spaces, influencing applications in functional analysis and dynamical systems.
Relationship With Other Topological Concepts
A closed set contains all its limit points and serves as a fundamental concept in topology, often forming the complement of an open set in a topological space. A nowhere dense set, by contrast, has an empty interior closure and is closely related to meager sets and Baire category, indicating it is "small" or "thin" within the space. The relationship between these sets reveals that every nowhere dense set is necessarily contained in a closed set with empty interior, connecting density, closure, and interior properties crucial to understanding topological structure and category theory.
Summary and Conclusion
A closed set contains all its limit points and forms a complete boundary within a topological space, while a nowhere dense set has an empty interior and does not contain any open subsets, making it topologically small. In summary, closed sets often have substantial topological structure, whereas nowhere dense sets are sparse and fail to densely occupy any open region. Understanding their distinctions is crucial for analyzing set properties in topology, measure theory, and functional analysis.
Closed set Infographic
 libterm.com
libterm.com