Sheaf theory provides a powerful framework for systematically associating algebraic data to topological spaces, enabling the study of local-to-global properties in mathematics. It is essential in fields such as algebraic geometry, differential topology, and complex analysis where it helps in understanding how local information can be patched together to form global structures. Explore the rest of this article to discover how sheaf theory can deepen your understanding of advanced mathematical concepts.
Table of Comparison
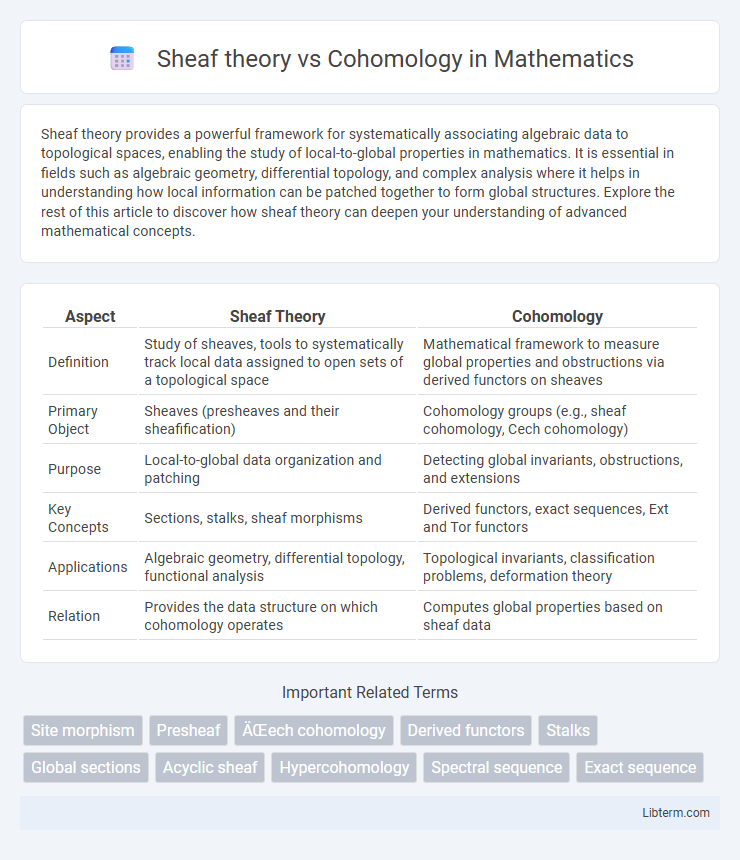
| Aspect | Sheaf Theory | Cohomology |
|---|---|---|
| Definition | Study of sheaves, tools to systematically track local data assigned to open sets of a topological space | Mathematical framework to measure global properties and obstructions via derived functors on sheaves |
| Primary Object | Sheaves (presheaves and their sheafification) | Cohomology groups (e.g., sheaf cohomology, Cech cohomology) |
| Purpose | Local-to-global data organization and patching | Detecting global invariants, obstructions, and extensions |
| Key Concepts | Sections, stalks, sheaf morphisms | Derived functors, exact sequences, Ext and Tor functors |
| Applications | Algebraic geometry, differential topology, functional analysis | Topological invariants, classification problems, deformation theory |
| Relation | Provides the data structure on which cohomology operates | Computes global properties based on sheaf data |
Introduction to Sheaf Theory and Cohomology
Sheaf theory provides a framework for systematically associating algebraic data to open sets of a topological space, enabling local-to-global analysis essential in modern geometry and topology. Cohomology arises as a powerful tool to measure the obstructions to gluing local data into a global object, often computed via derived functors applied to sheaves. Understanding sheaf theory is foundational for grasping cohomology, as it organizes local sections and their compatibility, laying the groundwork for advanced applications in algebraic geometry, differential topology, and complex analysis.
Historical Origins and Motivation
Sheaf theory originated in the mid-20th century through the work of Jean Leray, who introduced sheaves to study topological spaces by systematically organizing local data, while cohomology developed earlier as an algebraic tool to classify and measure global properties of spaces. The motivation behind sheaf theory was to provide a unified framework for extending local information to global contexts, addressing limitations in existing topological and analytic methods. Cohomology, particularly de Rham and Cech cohomology, aimed to capture invariants that distinguish topological spaces, ultimately influencing the formalization and expansion of sheaf-theoretic techniques.
Fundamental Concepts of Sheaf Theory
Sheaf theory centers on systematically organizing local data attached to open subsets of a topological space, using presheaves and sheaves to ensure compatible and consistent information across overlapping regions. Key concepts include stalks, which capture local behavior at points, and sheaf morphisms that preserve this structure. Cohomology leverages sheaf theory to compute global invariants by analyzing the obstructions in patching local sections, linking local-to-global principles in topology and algebraic geometry.
Basic Principles of Cohomology
Cohomology is a powerful mathematical tool used to study and classify topological spaces by assigning algebraic invariants that capture their global properties. It extends sheaf theory by systematically analyzing the global sections and their obstructions, enabling the computation of cohomology groups that reveal topological and geometric structures. Key principles of cohomology involve constructing cochain complexes, defining coboundary operators, and interpreting the resulting cohomology groups as measures of the failure to solve certain extension problems within sheaves.
Key Differences Between Sheaf Theory and Cohomology
Sheaf theory provides a framework for systematically tracking locally defined data attached to open sets of a topological space, while cohomology offers a global invariant that measures the failure to glue local data into a global section. Sheaves serve as the foundational objects that assign algebraic structures to open sets, whereas cohomology groups are derived from these sheaves to extract topological information about spaces. The key difference lies in sheaf theory's role in organizing local information and cohomology's role in capturing global topological properties through derived functors.
Interconnections: Sheaf Cohomology
Sheaf theory provides a framework for systematically tracking locally defined algebraic data on topological spaces, while cohomology serves as a powerful tool for measuring global properties derived from such local information. Sheaf cohomology specifically bridges these concepts by assigning cohomological invariants to sheaves, revealing obstructions to patching local data into global sections. This interplay is fundamental in algebraic geometry and topology, enabling deep insights into the structure of varieties, manifolds, and complex spaces.
Applications in Algebraic Geometry
Sheaf theory provides a systematic framework to study local geometric data and their global properties, serving as a foundational tool in algebraic geometry. Cohomology applies sheaf theory to calculate invariants that capture topological and algebraic information about varieties, such as the number of global sections and obstruction classes. Together, these concepts enable the classification of algebraic varieties, the analysis of line bundles, and the understanding of complex structures through techniques like Cech cohomology and derived functors.
Roles in Topology and Other Mathematical Fields
Sheaf theory provides a framework for systematically tracking local data attached to open sets in a topological space, facilitating the study of local-to-global principles, while cohomology offers algebraic invariants that measure global topological features such as holes and obstructions. In topology, sheaf theory organizes local information that cohomology groups then assemble into global invariants, enabling deep analysis of complex spaces like manifolds and algebraic varieties. Beyond topology, sheaf theory and cohomology play critical roles in algebraic geometry, differential geometry, and number theory, underpinning major theories like Hodge theory and the proof of the Weil conjectures.
Computational Approaches and Techniques
Sheaf theory provides a structured framework for local-to-global data analysis, enabling the encoding of variable local information across topological spaces, which is critical for computational methods in geometry and data science. Computational approaches to sheaf theory typically involve the construction of sheaf cohomology groups through Cech cohomology, cellular sheaves, or derived functor techniques, facilitating algorithmic implementations that compute global sections or obstructions. Cohomology, often computed via chain complexes and spectral sequences, complements these techniques by enabling effective calculations of topological invariants and detecting global properties through computational homological algebra methods applied in software such as SageMath or Macaulay2.
Future Directions and Open Problems
Future directions in sheaf theory and cohomology emphasize the development of computational methods for higher-dimensional data analysis and the integration of derived categories with topological data analysis. Open problems include the classification of perverse sheaves on singular spaces and the extension of cohomological techniques to non-abelian contexts, challenging current frameworks. Advances in these areas aim to deepen the understanding of geometric structures and foster applications in mathematical physics and complex systems.
Sheaf theory Infographic
 libterm.com
libterm.com