Cohomology is a fundamental tool in algebraic topology that provides a way to classify and measure the shape and structure of topological spaces through algebraic invariants. It captures global properties by assigning algebraic objects like groups or rings to spaces, allowing for deep insights into their geometric and topological features. Explore the rest of the article to understand how cohomology can enhance your study of mathematical spaces.
Table of Comparison
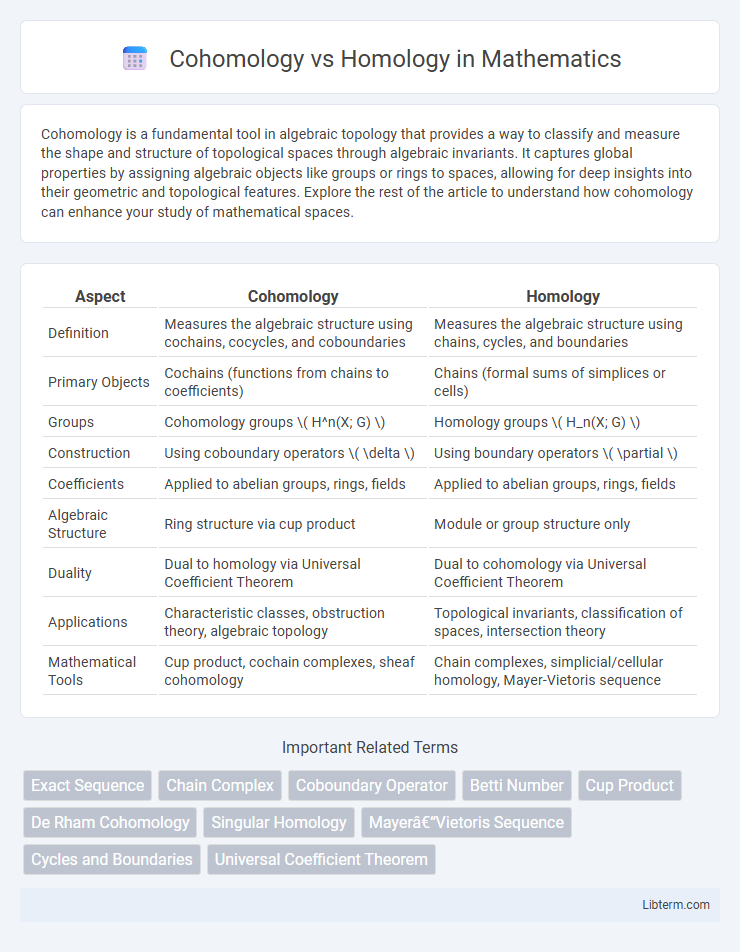
| Aspect | Cohomology | Homology |
|---|---|---|
| Definition | Measures the algebraic structure using cochains, cocycles, and coboundaries | Measures the algebraic structure using chains, cycles, and boundaries |
| Primary Objects | Cochains (functions from chains to coefficients) | Chains (formal sums of simplices or cells) |
| Groups | Cohomology groups \( H^n(X; G) \) | Homology groups \( H_n(X; G) \) |
| Construction | Using coboundary operators \( \delta \) | Using boundary operators \( \partial \) |
| Coefficients | Applied to abelian groups, rings, fields | Applied to abelian groups, rings, fields |
| Algebraic Structure | Ring structure via cup product | Module or group structure only |
| Duality | Dual to homology via Universal Coefficient Theorem | Dual to cohomology via Universal Coefficient Theorem |
| Applications | Characteristic classes, obstruction theory, algebraic topology | Topological invariants, classification of spaces, intersection theory |
| Mathematical Tools | Cup product, cochain complexes, sheaf cohomology | Chain complexes, simplicial/cellular homology, Mayer-Vietoris sequence |
Introduction to Cohomology and Homology
Homology and cohomology are fundamental concepts in algebraic topology, used to analyze the structure of topological spaces by associating algebraic invariants. Homology assigns a sequence of abelian groups or modules to a space, measuring the presence of holes of various dimensions through cycles and boundaries. Cohomology, often viewed as the dual theory to homology, assigns cochain complexes and provides richer algebraic structures like cup products, enabling finer distinctions in topological spaces.
Historical Background and Development
Homology originated in the early 20th century through the work of Henri Poincare, providing a way to classify topological spaces by studying cycles and boundaries. Cohomology developed later as a dual theory, introduced by Elie Cartan and further formalized by Henri Cartan and Jean-Pierre Serre, enhancing algebraic topology with ring and module structures. These theories evolved to become fundamental tools in modern mathematics, bridging topology, algebra, and geometry.
Fundamental Concepts and Definitions
Homology measures the presence of holes in topological spaces by analyzing cycles and boundaries within chain complexes, assigning algebraic structures such as groups to these features. Cohomology, on the other hand, reverses this perspective by focusing on cochains, coboundaries, and cocycles, yielding cohomology groups that provide additional algebraic invariants often equipped with ring structures. Both fundamental theories serve as dual tools in algebraic topology, capturing essential information about spaces through sequences of abelian groups and exact sequences.
Algebraic Structures: Chain vs. Cochain Complexes
Homology deals with chain complexes consisting of sequences of abelian groups or modules connected by boundary operators, capturing cycles and boundaries within topological spaces. Cohomology involves cochain complexes, which are dual to chain complexes and use coboundary operators to define cocycles and coboundaries, allowing for the construction of cohomology rings through cup products. The algebraic structures highlight homology's focus on detecting holes via chains, while cohomology's cochain complexes provide a richer algebraic framework with ring structures essential for classifying and analyzing topological invariants.
Key Differences Between Homology and Cohomology
Homology groups measure the presence of "holes" in a topological space by associating cycles and boundaries, capturing geometric features such as connectedness, loops, and voids. Cohomology groups, on the other hand, assign algebraic structures to spaces by mapping chains to coefficient groups, providing dual information that facilitates cup products and supports richer algebraic operations. Key differences include that homology is covariant with respect to continuous maps, while cohomology is contravariant, and cohomology often has a ring structure, enabling more refined invariants for topological classification.
Applications in Topology and Geometry
Cohomology provides powerful tools for classifying topological spaces by associating algebraic invariants such as cohomology rings, which capture additional structure like cup products not detected by homology. Homology groups measure holes in spaces directly, facilitating computations of Betti numbers and enabling geometric applications related to connectivity and shape analysis. Both theories are essential in differential geometry, with cohomology often used for characteristic classes and homology applied in Morse theory and manifold invariants.
Duality Principles: Universal Coefficient and Poincaré Duality
Cohomology and homology are connected through duality principles that provide deep insights into topological spaces. The Universal Coefficient Theorem establishes a relationship between homology and cohomology groups by expressing cohomology as the hom-functor applied to homology, enabling computations of cohomology from known homology data. Poincare Duality further links k-dimensional homology groups to (n-k)-dimensional cohomology groups in an n-dimensional orientable manifold, highlighting a fundamental symmetry in algebraic topology.
Computational Methods and Tools
Computational methods for homology often utilize efficient algorithms like persistent homology to analyze topological features in data, implemented in tools such as GUDHI and Dionysus. Cohomology computations typically involve cochain complexes and employ software like CHomP and Perseus to extract dual algebraic invariants that enhance feature detection and classification. Advances in computational topology increasingly integrate both homology and cohomology frameworks to improve the analysis of high-dimensional datasets and optimize performance in applications such as sensor networks and data mining.
Advantages and Limitations of Each Theory
Cohomology offers powerful tools for distinguishing topological spaces through the use of cochains, cocycles, and coboundaries, enabling a richer algebraic structure with ring and module properties that facilitate computations in algebraic topology. Homology provides a more geometric and intuitive approach to analyzing spaces by examining cycles and boundaries, which helps identify holes and connectedness but may lack the additional algebraic structures found in cohomology. While cohomology can be more computationally intensive and abstract, making it less accessible for simple applications, homology is often easier to compute but may fail to capture finer topological invariants detectable by cohomology's dual perspective.
Future Directions and Open Problems
Future directions in cohomology and homology emphasize the development of computational techniques for higher-dimensional data analysis and the exploration of their applications in string theory and quantum computing. Open problems include refining the understanding of spectral sequences convergence, advancing generalized (co)homology theories such as motivic and equivariant frameworks, and resolving conjectures related to the relationship between homological invariants and geometric structures. Integrating machine learning with topological data analysis could revolutionize approaches to persistent homology and cohomology, expanding their impact across mathematics and applied sciences.
Cohomology Infographic
 libterm.com
libterm.com