Scheme is a minimalist dialect of the Lisp programming language, emphasizing a clean and simple design with powerful features like first-class procedures and lexical scoping. Its unique approach to syntax and semantics enables developers to write concise and elegant code for both academic research and practical applications. Explore the rest of the article to discover how Scheme can enhance your programming skills and problem-solving techniques.
Table of Comparison
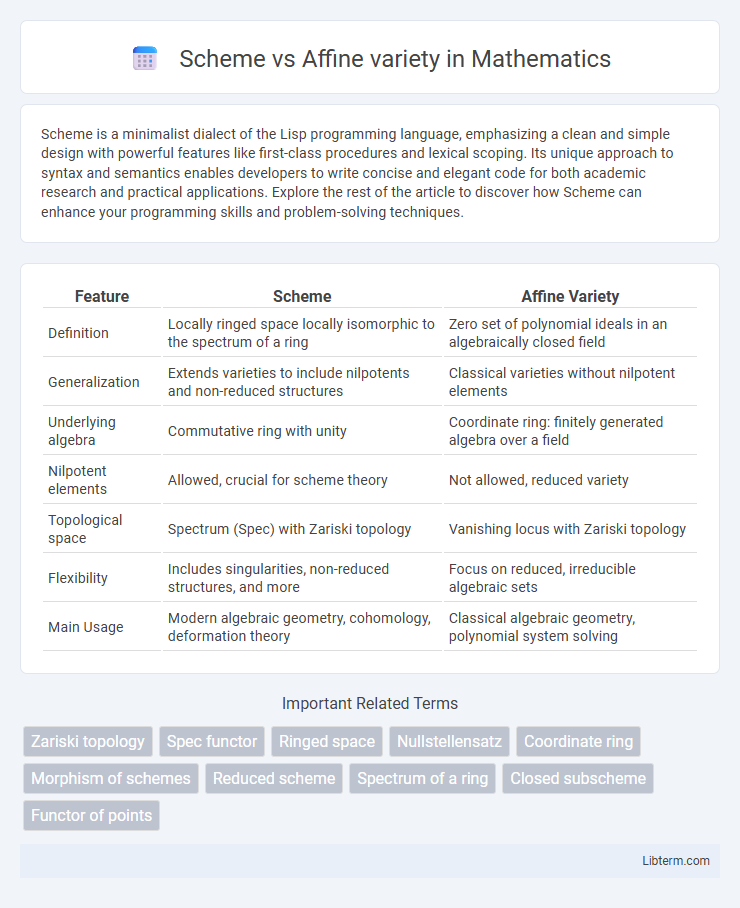
| Feature | Scheme | Affine Variety |
|---|---|---|
| Definition | Locally ringed space locally isomorphic to the spectrum of a ring | Zero set of polynomial ideals in an algebraically closed field |
| Generalization | Extends varieties to include nilpotents and non-reduced structures | Classical varieties without nilpotent elements |
| Underlying algebra | Commutative ring with unity | Coordinate ring: finitely generated algebra over a field |
| Nilpotent elements | Allowed, crucial for scheme theory | Not allowed, reduced variety |
| Topological space | Spectrum (Spec) with Zariski topology | Vanishing locus with Zariski topology |
| Flexibility | Includes singularities, non-reduced structures, and more | Focus on reduced, irreducible algebraic sets |
| Main Usage | Modern algebraic geometry, cohomology, deformation theory | Classical algebraic geometry, polynomial system solving |
Introduction to Schemes and Affine Varieties
Affine varieties are fundamental objects in algebraic geometry defined as the solution sets of polynomial equations over algebraically closed fields, characterized by their coordinate rings as finitely generated reduced algebras. Schemes generalize affine varieties by allowing the study of algebraic geometry over arbitrary rings and incorporating nilpotent elements, providing a unified framework through locally ringed spaces constructed from spectra of rings. The introduction to schemes emphasizes their local nature via affine schemes, which extend affine varieties by capturing richer geometric and algebraic structures beyond classical varieties.
Historical Development in Algebraic Geometry
The historical development of schemes revolutionized algebraic geometry by generalizing classical varieties and allowing for a more flexible framework to handle singularities and arithmetic phenomena. Affine varieties, rooted in the 19th century, represent the basic building blocks defined by polynomial equations over algebraically closed fields. The introduction of scheme theory by Alexander Grothendieck in the 1960s extended these concepts by incorporating prime spectra of rings, enabling a unified treatment of geometry and number theory that surpassed the limitations of affine varieties.
Definition and Basic Concepts of Affine Varieties
An affine variety is a fundamental algebraic set defined as the common zero locus of a set of polynomial equations over an algebraically closed field, forming a closed subset in affine space. Unlike schemes, which generalize varieties by incorporating nilpotent elements and gluing spectra of rings, affine varieties correspond strictly to prime ideals in polynomial rings and ensure reduced, irreducible algebraic structures. The coordinate ring of an affine variety captures its geometric properties through the quotient of the polynomial ring by the ideal of polynomials vanishing on the variety, enabling a concrete connection between algebra and geometry.
Formal Definition and Structure of Schemes
Schemes are defined as locally ringed spaces that are locally isomorphic to spectra of commutative rings, providing a unifying framework for algebraic geometry that generalizes affine varieties. Affine varieties correspond to prime spectra of finitely generated reduced algebras over algebraically closed fields, whereas schemes allow for nilpotent elements and arbitrary commutative rings, capturing more geometric phenomena. This formal structure of schemes incorporates both topological and sheaf-theoretic data, enabling the study of singularities, morphisms, and base changes in a more flexible categorical context than classical affine varieties.
Key Differences: Scheme vs Affine Variety
Schemes generalize affine varieties by incorporating nilpotent elements in their structure sheaf, allowing them to capture more subtle geometric information beyond reduced varieties. Affine varieties correspond to prime ideals in polynomial rings over algebraically closed fields, whereas schemes are locally ringed spaces constructed from spectra of arbitrary commutative rings, enabling the study of singularities and non-reduced structures. The flexibility of schemes facilitates advanced concepts like gluing affine patches and handling arithmetic properties, which affine varieties cannot address comprehensively.
Topological Properties Compared
Affine varieties possess the Zariski topology characterized by closed sets defined as zero loci of polynomial ideals, which while coarser, ensures every nonempty open subset is dense. Schemes generalize affine varieties by gluing spectra of rings, inheriting spectral topologies that are sober and quasi-compact but may not be Hausdorff, allowing finer local structures and nilpotent elements to influence the topology. The spectrum of a ring in a scheme has a basis of distinguished open sets revealing more intricate topological nuances compared to the comparatively rigid topology of affine varieties, facilitating advanced geometric constructions.
Functorial Perspectives and Representability
Scheme theory generalizes affine varieties by representing geometric objects as functors from commutative rings to sets, capturing both classical points and nilpotent elements through the functor of points. Affine varieties correspond to schemes representable by finitely generated reduced k-algebras, while schemes extend representability to arbitrary commutative rings, enabling the treatment of singularities and non-reduced structures. From the functorial perspective, schemes provide a fully faithful embedding into the category of functors, ensuring that geometric properties translate into algebraic representability conditions.
Main Examples Illustrating Both Concepts
The affine variety defined by the vanishing of polynomials such as \(x^2 + y^2 - 1 = 0\) in \(\mathbb{A}^2\) exemplifies classical algebraic geometry, while the scheme \(\text{Spec}(\mathbb{C}[x,y]/(x^2 + y^2 - 1))\) incorporates additional structure like nilpotent elements, allowing finer study of singularities and local behavior. A key example contrasting schemes and varieties is the spectrum of a ring with nilpotent elements, such as \(\text{Spec}(\mathbb{C}[x]/(x^2))\), which is a non-reduced scheme with no affine variety counterpart. The ability of schemes to model infinitesimal data and more general geometric phenomena extends the classical notion of affine varieties beyond reduced and irreducible algebraic sets.
Applications in Modern Algebraic Geometry
Schemes generalize affine varieties by incorporating nilpotent elements and allowing a more flexible structure sheaf, enabling the study of singularities and arithmetic properties in algebraic geometry. Affine varieties serve as the foundation for classical algebraic geometry, but schemes extend their applications to encompass more general base rings and better handle geometric objects over non-algebraically closed fields. Modern algebraic geometry leverages schemes to analyze moduli spaces, deformation theory, and arithmetic geometry problems, whereas affine varieties mainly focus on polynomial solution sets over algebraically closed fields.
Conclusion: When to Use Schemes or Affine Varieties
Schemes provide a more flexible and general framework than affine varieties, allowing the study of geometric objects with nilpotent elements and singularities, which is essential in modern algebraic geometry and number theory. Affine varieties are suitable for classical algebraic geometry problems over algebraically closed fields, offering a simpler and more intuitive language for concrete geometric intuition and computations. Use schemes when dealing with general base rings, singular spaces, or arithmetic geometry, and prefer affine varieties for explicit computations and problems over algebraically closed fields.
Scheme Infographic
 libterm.com
libterm.com