A sigma-algebra is a collection of subsets of a given set that is closed under countable unions, countable intersections, and complements, forming a foundational structure in measure theory and probability. Understanding the properties and applications of sigma-algebras is crucial for developing measures, integrating functions, and defining probability spaces. Explore the rest of the article to deepen your grasp of sigma-algebras and their role in mathematical analysis.
Table of Comparison
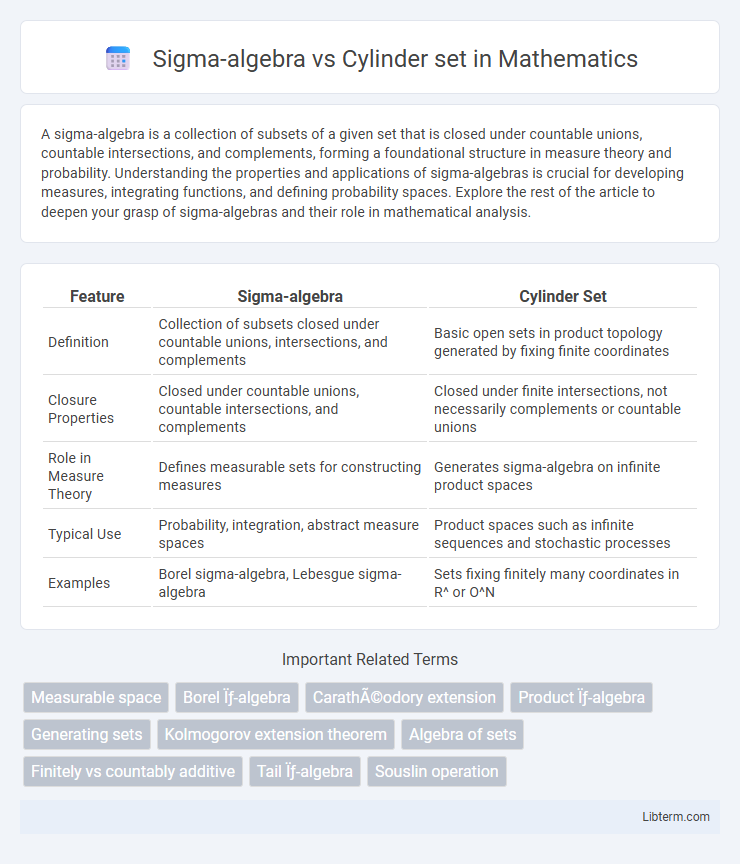
| Feature | Sigma-algebra | Cylinder Set |
|---|---|---|
| Definition | Collection of subsets closed under countable unions, intersections, and complements | Basic open sets in product topology generated by fixing finite coordinates |
| Closure Properties | Closed under countable unions, countable intersections, and complements | Closed under finite intersections, not necessarily complements or countable unions |
| Role in Measure Theory | Defines measurable sets for constructing measures | Generates sigma-algebra on infinite product spaces |
| Typical Use | Probability, integration, abstract measure spaces | Product spaces such as infinite sequences and stochastic processes |
| Examples | Borel sigma-algebra, Lebesgue sigma-algebra | Sets fixing finitely many coordinates in R^ or O^N |
Introduction to Sigma-Algebra and Cylinder Sets
Sigma-algebras are collections of subsets closed under countable unions, intersections, and complements, forming the foundational structure in measure theory for defining measurable spaces. Cylinder sets are specific subsets used primarily in product spaces, generated by fixing coordinates in a finite number of dimensions, serving as building blocks for sigma-algebras in infinite-dimensional spaces. Understanding the interplay between sigma-algebras and cylinder sets is essential for constructing measures on complex spaces like function or sequence spaces.
Fundamental Concepts of Sigma-Algebra
A sigma-algebra is a collection of subsets closed under countable unions, countable intersections, and complements, forming the foundational structure in measure theory. Cylinder sets, often used in product spaces, serve as generating sets that form the sigma-algebra by defining measurable rectangles based on finite-dimensional coordinate projections. Understanding sigma-algebras is crucial for defining measures and measurable functions, where cylinder sets provide a concrete example of how these fundamental concepts operate in infinite-dimensional spaces.
Defining Cylinder Sets in Measure Theory
Cylinder sets serve as the foundational building blocks in measure theory for defining product sigma-algebras, especially in infinite-dimensional spaces. A cylinder set is constructed by specifying measurable subsets in a finite number of coordinate spaces while allowing variations in all other coordinates, enabling effective extension of finite-dimensional measures to infinite dimensions. These sets generate the smallest sigma-algebra, known as the cylinder sigma-algebra, which is crucial for defining measures on spaces like function spaces or sequences.
Key Properties of Sigma-Algebras
A sigma-algebra is a collection of sets closed under countable unions, countable intersections, and complements, ensuring the structure supports well-defined probability measures. Cylinder sets form a base for sigma-algebras in product spaces, specifically constructed from finite-dimensional projections, but they themselves are not sigma-algebras unless closed under the mentioned operations. The key property of sigma-algebras is their closure under these operations, which allows for rigorous manipulation and measure definition in infinite-dimensional settings.
Structural Features of Cylinder Sets
Cylinder sets are fundamental building blocks in the construction of product sigma-algebras, characterized by fixing finite coordinates while allowing variations in infinite others. These sets exhibit a rectangular structure in product spaces, where each coordinate projection corresponds to measurable sets in individual factor spaces. This finite-dimensional segmentation enables the extension of measure-theoretic properties from simple factors to complex infinite-dimensional structures in probability and topology.
Sigma-Algebras: Role in Probability and Measure
Sigma-algebras are fundamental in probability theory and measure theory as they provide the structured collection of subsets over which measures, including probability measures, are defined. Unlike cylinder sets, which are specifically constructed for product spaces to facilitate finite-dimensional projections, sigma-algebras ensure closure under countable unions, intersections, and complements, enabling rigorous handling of infinite-dimensional events. Their role is crucial for defining measurable spaces that allow the assignment of probabilities and measures consistently across complex event structures.
Cylinder Sets in Product Spaces
Cylinder sets form the foundational building blocks in product spaces by defining measurable rectangles based on finite coordinate projections. They generate the smallest sigma-algebra, known as the product sigma-algebra, ensuring measurability across infinite-dimensional spaces. Their structure is crucial for extending measures and constructing probability measures on infinite product spaces.
Differences Between Sigma-Algebra and Cylinder Set
Sigma-algebra is a collection of sets closed under countable unions, countable intersections, and complements, forming the foundation for measure theory and probability. Cylinder sets, on the other hand, are specific subsets generated by fixing a finite number of coordinates in a product space, primarily used in infinite-dimensional spaces like function spaces. Unlike sigma-algebras, cylinder sets do not necessarily form a sigma-algebra themselves but serve as generating sets for sigma-algebras in product spaces or infinite-dimensional contexts.
Applications in Probability and Real Analysis
Sigma-algebras provide a fundamental framework for defining measurable spaces essential in probability theory, enabling the rigorous formulation of probability measures and integration. Cylinder sets form the building blocks for product sigma-algebras, which are crucial in analyzing stochastic processes and infinite-dimensional spaces in real analysis. Both concepts facilitate the study of measurable functions and convergence, underpinning advanced applications in fields like statistical mechanics and functional analysis.
Summary and Comparative Insights
Sigma-algebras provide a foundational framework in measure theory, encompassing collections of sets closed under countable unions, intersections, and complements, enabling rigorous definition of measures. Cylinder sets, often used in product spaces, serve as generating sets for sigma-algebras, characterized by fixing finitely many coordinates while allowing arbitrary values elsewhere. The key comparative insight is that cylinder sets form the building blocks for sigma-algebras in infinite-dimensional spaces, allowing extension from simple, finite-dimensional events to complex measurable structures essential for probability and functional analysis.
Sigma-algebra Infographic
 libterm.com
libterm.com