Crystalline cohomology is a powerful tool in algebraic geometry used to study the properties of algebraic varieties over fields of positive characteristic. It provides a way to lift problems from characteristic p to characteristic zero, enabling the computation of invariants that are otherwise challenging to access. Explore the rest of the article to deepen your understanding of crystalline cohomology and its applications.
Table of Comparison
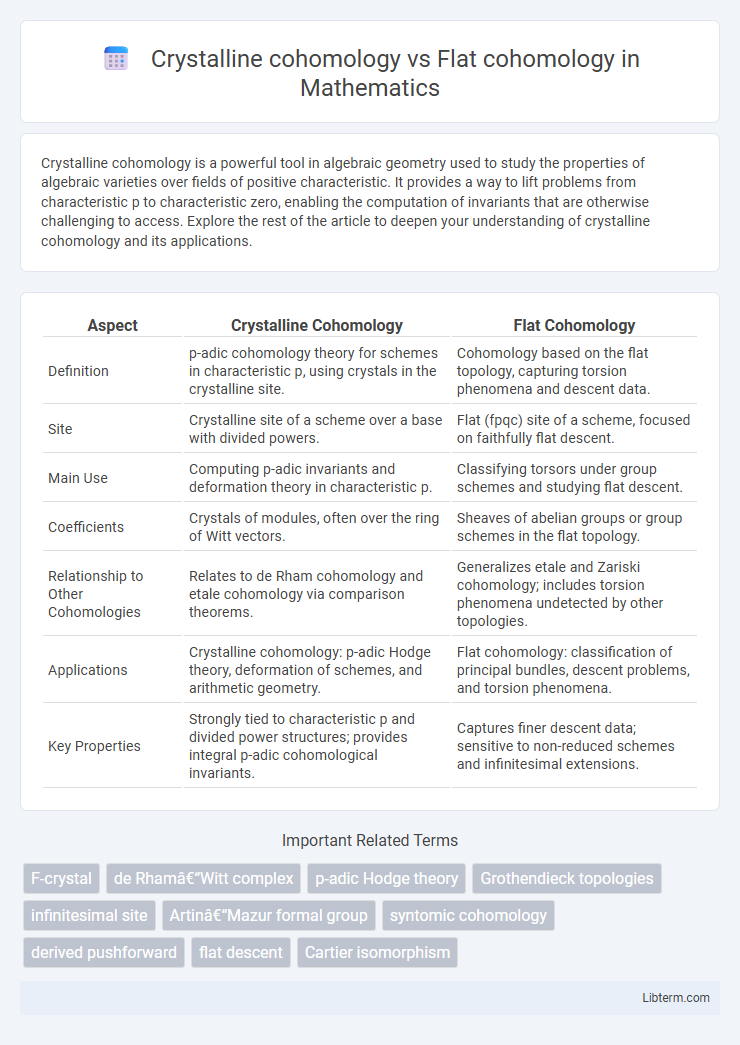
| Aspect | Crystalline Cohomology | Flat Cohomology |
|---|---|---|
| Definition | p-adic cohomology theory for schemes in characteristic p, using crystals in the crystalline site. | Cohomology based on the flat topology, capturing torsion phenomena and descent data. |
| Site | Crystalline site of a scheme over a base with divided powers. | Flat (fpqc) site of a scheme, focused on faithfully flat descent. |
| Main Use | Computing p-adic invariants and deformation theory in characteristic p. | Classifying torsors under group schemes and studying flat descent. |
| Coefficients | Crystals of modules, often over the ring of Witt vectors. | Sheaves of abelian groups or group schemes in the flat topology. |
| Relationship to Other Cohomologies | Relates to de Rham cohomology and etale cohomology via comparison theorems. | Generalizes etale and Zariski cohomology; includes torsion phenomena undetected by other topologies. |
| Applications | Crystalline cohomology: p-adic Hodge theory, deformation of schemes, and arithmetic geometry. | Flat cohomology: classification of principal bundles, descent problems, and torsion phenomena. |
| Key Properties | Strongly tied to characteristic p and divided power structures; provides integral p-adic cohomological invariants. | Captures finer descent data; sensitive to non-reduced schemes and infinitesimal extensions. |
Introduction to Crystalline and Flat Cohomology
Crystalline cohomology provides a powerful tool for studying the algebraic structure of schemes in characteristic p by capturing infinitesimal deformations through PD-thickenings and extending de Rham cohomology concepts. Flat cohomology, on the other hand, utilizes the flat (fpqc) topology to classify torsors under group schemes and detect obstructions in descent problems, making it crucial for questions in arithmetic geometry and deformation theory. Both theories offer complementary approaches to understanding scheme cohomology by addressing different aspects of algebraic and geometric structure in positive characteristic settings.
Historical Context and Motivation
Crystalline cohomology emerged in the late 1960s as a tool to study algebraic varieties over fields of positive characteristic, addressing limitations in etale and de Rham cohomologies for such settings. Flat cohomology, rooted in Grothendieck's development of the fppf topology, was motivated by the need to classify torsors under group schemes and extend cohomological methods to more general sheaves beyond etale covers. Both cohomology theories reflect foundational efforts to understand algebraic structures in characteristic p and generalize cohomological approaches in algebraic geometry.
Fundamental Definitions and Concepts
Crystalline cohomology is a p-adic cohomology theory used to study algebraic varieties over fields of positive characteristic, defined via the crystalline site and divided power structures that capture infinitesimal thickenings. Flat cohomology, on the other hand, arises from the fppf (faithfully flat and finitely presented) topology, focusing on sheaf cohomology with respect to flat morphisms, and is crucial for understanding torsors and descent theory. Both cohomologies serve as tools to analyze different geometric and arithmetic properties, with crystalline cohomology emphasizing deformation theory and flat cohomology emphasizing general descent and flat group schemes.
Key Differences Between Crystalline and Flat Cohomology
Crystalline cohomology, designed for schemes in characteristic p, captures p-adic phenomena by working with divided power thickenings and provides a robust framework for understanding infinitesimal deformations. Flat cohomology, based on the fppf topology, is more flexible, enabling the study of torsors under flat group schemes and detecting obstructions related to flat descent and nontrivial extensions. Key differences include crystalline cohomology's focus on arithmetic geometry in characteristic p with a strong link to p-adic Hodge theory, while flat cohomology emphasizes the classification of principal bundles and has broader applications in descent theory and algebraic geometry over arbitrary bases.
Applications in Algebraic Geometry
Crystalline cohomology provides a powerful tool for studying algebraic varieties in characteristic p > 0 by capturing infinitesimal deformations and offering a p-adic analog of de Rham cohomology with strong ties to the theory of schemes and deformation theory. Flat cohomology, on the other hand, is instrumental in understanding torsors under group schemes and classifying principal bundles, impacting the study of moduli spaces and the Brauer group. Both cohomology theories contribute complementary insights into the structural and arithmetic properties of algebraic varieties, influencing topics like p-adic Hodge theory and descent problems in algebraic geometry.
Technical Framework: Schemes, Sheaves, and Topologies
Crystalline cohomology utilizes the crystalline site of a scheme, involving sheaves of PD (divided power) thickenings over a p-adic base, emphasizing infinitesimal extensions within characteristic p geometry. Flat cohomology, in contrast, relies on the fppf (faithfully flat and finitely presented) topology, using sheaves associated with flat morphisms to capture descent data and torsors under group schemes. Both theories operate on Grothendieck topologies but differ in their treatment of sheaf conditions and morphism classes, reflecting distinct technical frameworks tailored to their specific arithmetic and geometric applications.
Comparison of Cohomological Properties
Crystalline cohomology provides a powerful tool for studying smooth varieties in characteristic p by capturing p-adic Hodge structures and offering a well-behaved theory with Frobenius actions, while flat cohomology focuses on torsors under flat group schemes and handles more general, possibly singular, schemes. Crystalline cohomology is inherently linked to infinitesimal thickenings and deformation theory, yielding p-adically complete cohomology groups, whereas flat cohomology is flexible with respect to the flat topology and can detect nontrivial torsors that other cohomology theories might miss. Both theories have different exactness properties and spectral sequences, with crystalline cohomology exhibiting finer arithmetic structure and flat cohomology excelling in classifying algebraic structures such as line bundles and principal bundles on arbitrary base schemes.
Crystalline Cohomology: Strengths and Limitations
Crystalline cohomology excels in studying algebraic varieties over fields of positive characteristic by providing integral p-adic invariants that capture fine arithmetic information and facilitate comparison with de Rham cohomology in characteristic zero. Its strengths include robustness in handling singularities and compatibility with Frobenius actions, making it fundamental in p-adic Hodge theory and the study of deformation spaces. However, crystalline cohomology faces limitations in computational complexity and challenges with non-smooth schemes, where flat cohomology sometimes offers complementary insights through its broader topological framework.
Flat Cohomology: Strengths and Limitations
Flat cohomology excels in capturing geometric and arithmetic properties of schemes via flat morphisms, providing powerful tools for studying torsors under group schemes and addressing questions in deformation theory and descent. Its strengths lie in handling non-reduced schemes and providing finer distinctions compared to etale cohomology, yet it faces limitations such as computational complexity and challenges in explicit calculations due to the intricate nature of flat covers. While crystalline cohomology excels in p-adic Hodge theory and studying schemes in characteristic p, flat cohomology complements by offering a flexible framework applicable to broader classes of morphisms and cohomological problems.
Choosing the Right Cohomology Theory: Practical Criteria
Crystalline cohomology excels in studying smooth schemes over a perfect field of positive characteristic, providing powerful tools for lifting problems and p-adic Hodge theory due to its connection with de Rham cohomology. Flat cohomology is preferable when dealing with more general sheaves of groups, especially in settings requiring descent theory or dealing with torsors under flat group schemes, offering a flexible framework for non-smooth or non-reduced schemes. Practical criteria include the nature of the scheme (smooth vs. general), the characteristic of the base field, and the desired link to deformation or torsor classification problems, guiding the choice between crystalline and flat cohomology.
Crystalline cohomology Infographic
 libterm.com
libterm.com