The infimum of a set is the greatest value that is less than or equal to every element within that set, serving as a crucial concept in mathematical analysis and optimization. Understanding the properties of the infimum helps to solve problems related to bounds and limits in functions and sequences. Explore the rest of the article to deepen your grasp of infimum and its applications.
Table of Comparison
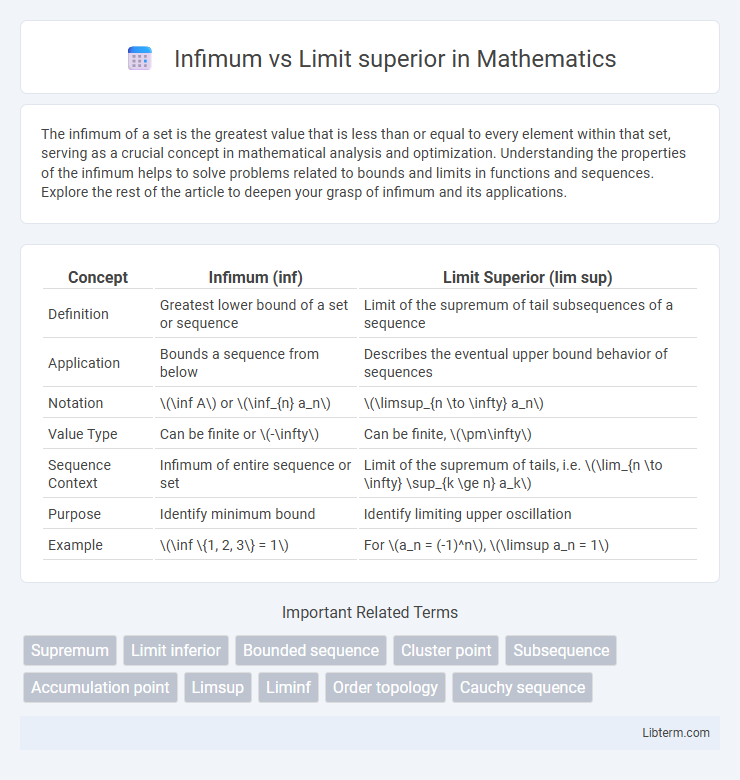
| Concept | Infimum (inf) | Limit Superior (lim sup) |
|---|---|---|
| Definition | Greatest lower bound of a set or sequence | Limit of the supremum of tail subsequences of a sequence |
| Application | Bounds a sequence from below | Describes the eventual upper bound behavior of sequences |
| Notation | \(\inf A\) or \(\inf_{n} a_n\) | \(\limsup_{n \to \infty} a_n\) |
| Value Type | Can be finite or \(-\infty\) | Can be finite, \(\pm\infty\) |
| Sequence Context | Infimum of entire sequence or set | Limit of the supremum of tails, i.e. \(\lim_{n \to \infty} \sup_{k \ge n} a_k\) |
| Purpose | Identify minimum bound | Identify limiting upper oscillation |
| Example | \(\inf \{1, 2, 3\} = 1\) | For \(a_n = (-1)^n\), \(\limsup a_n = 1\) |
Introduction to Infimum and Limit Superior
The infimum represents the greatest lower bound of a set, ensuring no element falls below this value, while the limit superior (lim sup) describes the supremum of the set of subsequential limits of a sequence. Infimum is crucial for bounding sequences from below and understanding convergence behavior in real analysis. Limit superior captures the eventual upper bound behavior of a sequence, playing a vital role in studying oscillations and convergence properties.
Fundamental Definitions
The infimum, or greatest lower bound, of a sequence is the highest value that is less than or equal to every term, ensuring it is the maximal lower constraint in the real number set. The limit superior, or lim sup, represents the smallest cluster point or limit of the supremum of the tail subsequences, capturing the eventual upper bounds that the sequence approaches infinitely often. These fundamental definitions differentiate infimum as a static bound from limit superior as a dynamic boundary describing long-term sequence behavior.
Key Differences Between Infimum and Limit Superior
The infimum represents the greatest lower bound of a set, ensuring no element lies below it, whereas the limit superior identifies the supremum of the set of subsequential limits in a sequence. Infimum applies broadly to sets as the minimal boundary, while limit superior specifically characterizes the long-term behavior of bounded sequences by capturing their largest cluster point. Unlike the infimum, limit superior concerns asymptotic sequence behavior and may vary depending on oscillations, making it crucial in convergence analysis and real analysis contexts.
Mathematical Notations Explained
The infimum (inf) of a sequence {a_n} represents the greatest lower bound, denoted as inf{a_n}, ensuring no element of the sequence is less than this value. The limit superior (lim sup) of {a_n} is expressed as lim sup_{n-} a_n, describing the supremum of the set of subsequential limits, capturing the highest cluster point of the sequence. Both infimum and limit superior are crucial in real analysis for bounding and characterizing the asymptotic behavior of sequences using precise mathematical notation.
Infimum: Properties and Examples
The infimum of a set, also known as the greatest lower bound, is the largest value that is less than or equal to every element in that set, unlike the limit superior which deals with the behavior of sequences. Properties of the infimum include its existence for any non-empty subset of real numbers that is bounded below and its role as the minimum value when it belongs to the set. For example, the infimum of the open interval (0,1) is 0, which serves as a lower bound but is not an element of the set, illustrating that the infimum may not always be attained within the set itself.
Limit Superior: Properties and Interpretation
Limit superior, or lim sup, represents the greatest accumulation point of a sequence, capturing the largest value subsequences approach infinitely often. It can be characterized as the smallest real number that is greater than or equal to the tail supremum values of the sequence. Essential properties include monotonicity in subsequences and the fact that lim sup always exists (possibly infinite) for bounded sequences, providing key insight into oscillatory or convergent behavior.
Relationships Between Infimum and Limit Superior
The infimum of a sequence represents the greatest lower bound of its values, while the limit superior (lim sup) captures the largest cluster point or subsequential limit. For any bounded sequence \((a_n)\), the infimum is always less than or equal to the limit superior, expressed as \(\inf a_n \leq \limsup a_n\). This inequality highlights that the limit superior reflects the sequence's asymptotic upper behavior, whereas the infimum indicates its minimal boundary.
Applications in Real Analysis
The concepts of infimum and limit superior play crucial roles in real analysis, particularly in understanding sequence behavior and measure theory. Infimum provides the greatest lower bound, essential in optimization problems and defining integrals, while limit superior captures the eventual upper bound of subsequences, aiding in characterizing convergence and oscillation patterns. Applications include proving theorems related to boundedness, analyzing series convergence, and studying function limits in metric spaces.
Common Mistakes and Misconceptions
Confusing the infimum with the limit superior often arises from misunderstanding their definitions: the infimum represents the greatest lower bound of a set, while the limit superior captures the largest subsequential limit of a sequence. A common mistake is assuming the limit superior always equals the supremum of the sequence's tail, neglecting the nuanced behavior of oscillating sequences. Misconceptions also include treating the infimum as a limit, which disregards that it may not be attainable or related to the sequence's convergence properties.
Summary and Conclusion
The infimum represents the greatest lower bound of a sequence, capturing its minimum accumulation point, while the limit superior identifies the least upper bound of all subsequential limits, reflecting the sequence's maximal cluster value. Understanding these concepts is crucial for analyzing convergence behavior in real analysis, as the infimum and limit superior bracket the range within which the sequence oscillates or stabilizes. They provide foundational tools for evaluating boundedness, limit points, and the overall structure of sequences in metric spaces.
Infimum Infographic
 libterm.com
libterm.com