The automorphism group represents all the symmetries of a mathematical structure, preserving its essential properties under transformations. Understanding this group provides deep insights into the object's internal structure and behavior across various fields, including algebra and geometry. Explore the rest of the article to discover how your knowledge of automorphism groups can unlock new perspectives in mathematical theory.
Table of Comparison
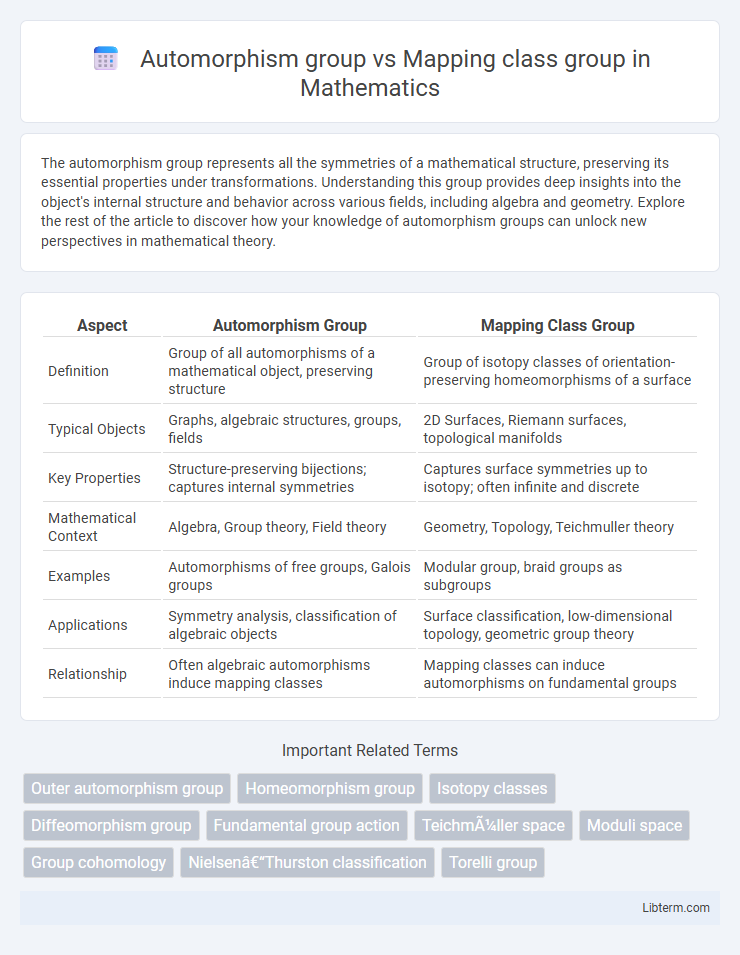
| Aspect | Automorphism Group | Mapping Class Group |
|---|---|---|
| Definition | Group of all automorphisms of a mathematical object, preserving structure | Group of isotopy classes of orientation-preserving homeomorphisms of a surface |
| Typical Objects | Graphs, algebraic structures, groups, fields | 2D Surfaces, Riemann surfaces, topological manifolds |
| Key Properties | Structure-preserving bijections; captures internal symmetries | Captures surface symmetries up to isotopy; often infinite and discrete |
| Mathematical Context | Algebra, Group theory, Field theory | Geometry, Topology, Teichmuller theory |
| Examples | Automorphisms of free groups, Galois groups | Modular group, braid groups as subgroups |
| Applications | Symmetry analysis, classification of algebraic objects | Surface classification, low-dimensional topology, geometric group theory |
| Relationship | Often algebraic automorphisms induce mapping classes | Mapping classes can induce automorphisms on fundamental groups |
Introduction to Symmetry in Mathematics
The automorphism group of a mathematical object consists of all structure-preserving bijections from the object to itself, encapsulating its intrinsic symmetries. In contrast, the mapping class group captures the symmetries of topological spaces, such as surfaces, up to isotopy, reflecting deformations rather than rigid motions. Both groups play crucial roles in understanding symmetry, with automorphism groups emphasizing algebraic invariance and mapping class groups focusing on geometric and topological equivalences.
Defining Automorphism Groups
Automorphism groups consist of all isomorphisms from a mathematical object to itself, preserving its structural properties such as group operations or graph connections. These groups capture the symmetries inherent in algebraic structures, topological spaces, or geometric objects by formalizing their self-maps that respect fundamental relations. Defining automorphism groups thus requires specifying the object's category and the nature of morphisms that maintain its defining characteristics.
Understanding Mapping Class Groups
Mapping class groups capture the isotopy classes of orientation-preserving homeomorphisms of a surface, playing a fundamental role in low-dimensional topology and geometric group theory. Unlike automorphism groups, which consist of all structure-preserving bijections of algebraic objects such as groups or graphs, mapping class groups describe the symmetries of surfaces up to continuous deformation. Understanding mapping class groups involves analyzing their action on curves, Teichmuller spaces, and their connections to braid groups and moduli spaces of Riemann surfaces.
Key Differences Between Automorphism and Mapping Class Groups
Automorphism groups consist of isomorphisms from a mathematical object to itself preserving its algebraic structure, while mapping class groups involve isotopy classes of homeomorphisms of surfaces, focusing on topological equivalences. The automorphism group emphasizes algebraic symmetries, often linked to group or field structures, whereas the mapping class group captures geometric and topological deformation classes, especially in surface topology and Teichmuller theory. Key differences include their domains--automorphisms act on abstract algebraic objects, and mapping class groups act on surfaces--and their role in understanding structural vs. geometric symmetries.
Algebraic Structures and Their Automorphisms
The automorphism group of an algebraic structure consists of all isomorphisms from the structure to itself, preserving its operations and relations, thus revealing its internal symmetries. The mapping class group arises in topology as the group of isotopy classes of homeomorphisms of a surface, encoding geometric symmetries with deep connections to algebraic structures via their fundamental groups. Studying the interplay between automorphism groups and mapping class groups enhances understanding of how algebraic invariants reflect topological transformations and geometric properties.
Topological Surfaces and Mapping Class Groups
The automorphism group of a topological surface captures all self-homeomorphisms that preserve the surface's structure, often realized as the group of isotopy classes of these homeomorphisms. In contrast, the mapping class group of a surface is defined as the group of isotopy classes of orientation-preserving homeomorphisms, providing key insights into the surface's moduli and Teichmuller spaces. Studying the interplay between automorphism groups and mapping class groups reveals the rich geometry and algebraic structures inherent to topological surfaces, especially in the classification of surface diffeomorphisms and their action on homology.
Group Actions: Automorphism vs Mapping Class
The Automorphism group acts on algebraic structures by permuting elements while preserving operations, capturing symmetries in abstract algebraic contexts. The Mapping Class group operates on topological surfaces, representing isotopy classes of orientation-preserving homeomorphisms, crucial for understanding surface diffeomorphisms and moduli spaces. Group actions of the Automorphism group are algebraic and rigid, whereas those of the Mapping Class group are topological and geometric, reflecting underlying structural differences.
Notable Examples and Applications
The automorphism group of a free group often provides critical insights into the structure of graphs and algebraic topology, where the outer automorphism group Out(F_n) serves as an essential object of study in geometric group theory. Mapping class groups, defined as the group of isotopy classes of orientation-preserving diffeomorphisms of a surface, are central to Teichmuller theory and 3-manifold topology, with applications including the classification of surfaces and the study of moduli spaces. Notable examples include the Nielsen-Thurston classification of mapping classes and the action of Out(F_n) on Culler-Vogtmann Outer space, both of which underpin key advancements in low-dimensional topology and geometric group theory.
Connections to Algebraic Topology and Geometry
The automorphism group of a topological space captures symmetries preserving its algebraic structure, often described by group actions on homology or fundamental groups, which are central objects in algebraic topology. The mapping class group, as the group of isotopy classes of orientation-preserving homeomorphisms of surfaces, encodes geometric deformations and is deeply linked to Teichmuller theory, moduli spaces, and hyperbolic geometry. Both groups serve as key tools in studying surface diffeomorphisms, fiber bundles, and the interplay between algebraic invariants and geometric structures.
Open Problems and Future Research Directions
The automorphism group of a mathematical structure, such as a graph or a group, encapsulates all symmetries preserving its algebraic or combinatorial properties, whereas the mapping class group captures isotopy classes of homeomorphisms of surfaces, central to low-dimensional topology. Open problems include understanding the precise relationship between automorphism groups and mapping class groups in higher-genus surfaces, as well as classifying their subgroup structures and rigidity phenomena. Future research directions explore the interaction of these groups with Teichmuller theory, geometric group theory, and dynamics, aiming to reveal new invariants and algorithmic methods for distinguishing mapping classes.
Automorphism group Infographic
 libterm.com
libterm.com