Derived functors extend the classical notion of functors in homological algebra to capture deeper structural information from chain complexes and their homology. They play a crucial role in computing Ext and Tor groups, which measure extensions and relations between modules beyond exact sequences. Explore the rest of this article to understand how derived functors impact modern algebraic methods and your mathematical toolkit.
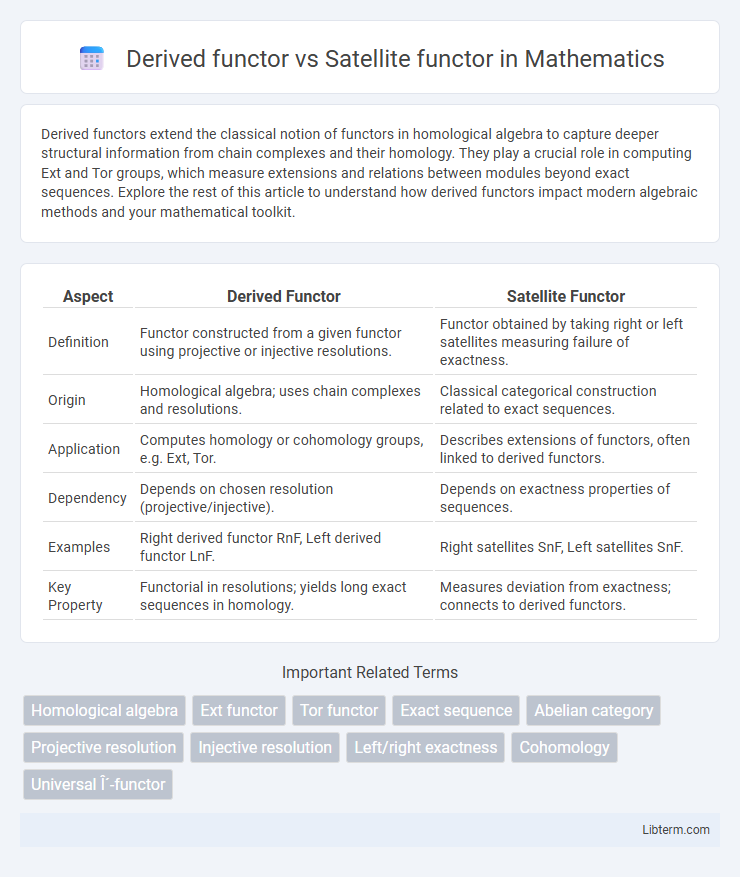
Table of Comparison
| Aspect | Derived Functor | Satellite Functor |
|---|---|---|
| Definition | Functor constructed from a given functor using projective or injective resolutions. | Functor obtained by taking right or left satellites measuring failure of exactness. |
| Origin | Homological algebra; uses chain complexes and resolutions. | Classical categorical construction related to exact sequences. |
| Application | Computes homology or cohomology groups, e.g. Ext, Tor. | Describes extensions of functors, often linked to derived functors. |
| Dependency | Depends on chosen resolution (projective/injective). | Depends on exactness properties of sequences. |
| Examples | Right derived functor RnF, Left derived functor LnF. | Right satellites SnF, Left satellites SnF. |
| Key Property | Functorial in resolutions; yields long exact sequences in homology. | Measures deviation from exactness; connects to derived functors. |
Introduction to Derived and Satellite Functors
Derived functors generalize the process of taking homology or cohomology by extending a functor to chain complexes, capturing higher-dimensional algebraic structures. Satellite functors arise from the failure of exactness in functors and measure the deviation by systematically associating objects in abelian categories, often constructed via projective or injective resolutions. Both derived and satellite functors play crucial roles in homological algebra by providing tools to compute and understand extensions, torsion, and other derived invariants.
Historical Development and Motivation
Derived functors emerged from homological algebra to generalize and compute right or left exact functors' failure to be exact, originally developed by Cartan and Eilenberg in the 1950s. Satellite functors were introduced by Grothendieck as an earlier, more geometric concept to capture similar notions of extending functors beyond exactness. Both concepts address the need to systematically study extensions and cohomological dimensions, with derived functors becoming more prevalent due to their robust formal framework in modern algebraic geometry and category theory.
Definitions: Derived Functor Explained
Derived functors are constructed from a given additive functor between abelian categories to systematically measure the failure of exactness, typically using projective or injective resolutions. They generalize the notion of applying a functor beyond its exactness limitations by extending it to a sequence of higher-dimensional functors, such as Ext and Tor in homological algebra. Satellite functors serve as precursors to derived functors, originally defined through exact sequences but later encompassed by the derived functor framework for more comprehensive homological analysis.
Understanding Satellite Functor: A Formal Overview
Satellite functors arise in homological algebra as tools to extend a given additive functor between abelian categories, capturing higher-dimensional information beyond the initial functor's image. They are defined using exact sequences and projective or injective resolutions, providing a systematic way to measure the failure of exactness in derived functors. Unlike derived functors that explicitly use resolutions to compute cohomology groups, satellite functors focus on formal properties and universal constructions to generalize functorial behavior in homological contexts.
Key Differences Between Derived and Satellite Functors
Derived functors originate from homological algebra as tools to extend additive functors to the derived category, capturing higher-dimensional homological information through exact sequences. Satellite functors generalize this concept by associating functors to any additive functor, focusing on constructing sequences that measure failure of exactness without necessarily requiring derived category structures. Key differences include that derived functors primarily relate to homology and cohomology theories using projective or injective resolutions, whereas satellite functors emphasize the extension of functors in more general additive categories, often being more flexible but less specific in homological contexts.
Applications in Homological Algebra
Derived functors, such as Ext and Tor, play a crucial role in Homological Algebra by measuring the failure of exactness in functors and providing tools for computations in module theory and sheaf cohomology. Satellite functors generalize derived functors by extending homological constructions to categories lacking enough projectives or injectives, broadening the scope of homological methods in algebra and topology. Both concepts facilitate the analysis of chain complexes and the extraction of algebraic invariants essential for classification problems and spectral sequence computations.
Examples Illustrating Derived Functors
Derived functors generalize and extend classical constructions like Ext and Tor, which arise from projective or injective resolutions in homological algebra, providing a systematic way to measure the failure of exactness in functors. For example, the Ext functor, derived from the Hom functor, computes extensions of modules and reveals hidden structural information about module categories, while the Tor functor, derived from the tensor product, captures torsion phenomena in modules. Satellite functors also arise by adjusting a given functor to create sequences reflecting homological behavior, but derived functors offer a more robust framework through resolution methods, widely used in computing sheaf cohomology, group cohomology, and other invariants in algebraic topology and algebraic geometry.
Examples Illustrating Satellite Functors
Satellite functors arise from taking the right or left derived functors of a suitable functor, typically extending homological constructions beyond exact sequences. For example, the classical Ext and Tor functors are satellite functors derived from Hom and Tensor functors, respectively, measuring extensions and torsion phenomena in modules. Another example includes the derived functors of inverse limit, called lim1 and higher lim functors, which serve as satellites capturing obstructions and higher cohomological information in inverse systems.
Interrelations: When Do Derived and Satellite Functors Coincide?
Derived functors and satellite functors coincide primarily when the underlying functor is half-exact and the category has enough projectives or injectives to compute these functors. In particular, for a left-exact functor, its right derived functors agree with the right satellite functors constructed via resolutions by projective objects. This equivalence extends to right-exact functors and their left derived functors, linking the computations of derived and satellite functors through specific exactness and existence of resolutions in abelian categories.
Conclusion: Choosing the Right Functor for Your Framework
Derived functors provide a robust framework for computing homological invariants in abelian categories, making them essential in contexts requiring exactness and depth, such as sheaf cohomology. Satellite functors, while closely related, offer a more general approach that can be applied in settings where projective or injective resolutions are unavailable or cumbersome. Selecting between derived and satellite functors depends on the categorical framework, the exactness properties needed, and the computational tools available within your algebraic or topological context.
Derived functor Infographic
 libterm.com
libterm.com