Jordan Normal Form reveals the structure of a linear operator by decomposing a matrix into Jordan blocks, simplifying complex eigenvalue problems. This canonical form is crucial for understanding generalized eigenvectors and matrix similarity transformations in linear algebra. Explore the detailed concepts and computations of Jordan Normal Form throughout the rest of the article.
Table of Comparison
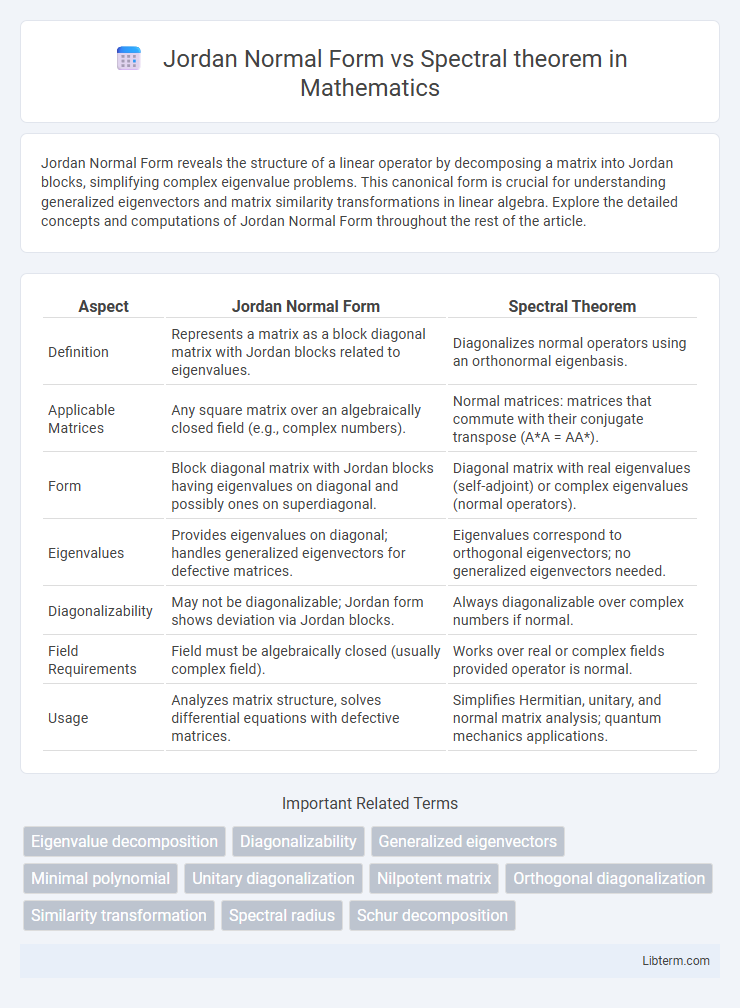
| Aspect | Jordan Normal Form | Spectral Theorem |
|---|---|---|
| Definition | Represents a matrix as a block diagonal matrix with Jordan blocks related to eigenvalues. | Diagonalizes normal operators using an orthonormal eigenbasis. |
| Applicable Matrices | Any square matrix over an algebraically closed field (e.g., complex numbers). | Normal matrices: matrices that commute with their conjugate transpose (A*A = AA*). |
| Form | Block diagonal matrix with Jordan blocks having eigenvalues on diagonal and possibly ones on superdiagonal. | Diagonal matrix with real eigenvalues (self-adjoint) or complex eigenvalues (normal operators). |
| Eigenvalues | Provides eigenvalues on diagonal; handles generalized eigenvectors for defective matrices. | Eigenvalues correspond to orthogonal eigenvectors; no generalized eigenvectors needed. |
| Diagonalizability | May not be diagonalizable; Jordan form shows deviation via Jordan blocks. | Always diagonalizable over complex numbers if normal. |
| Field Requirements | Field must be algebraically closed (usually complex field). | Works over real or complex fields provided operator is normal. |
| Usage | Analyzes matrix structure, solves differential equations with defective matrices. | Simplifies Hermitian, unitary, and normal matrix analysis; quantum mechanics applications. |
Introduction to Jordan Normal Form and Spectral Theorem
Jordan Normal Form provides a canonical matrix representation that reveals the structure of linear operators on finite-dimensional vector spaces by organizing eigenvalues and their generalized eigenspaces into Jordan blocks. The Spectral Theorem, applicable to normal operators on inner product spaces, guarantees diagonalization through an orthonormal basis of eigenvectors, ensuring the operator can be expressed as a sum of projections scaled by eigenvalues. Both concepts are fundamental in linear algebra, with Jordan Normal Form handling arbitrary operators and the Spectral Theorem specifically addressing normal operators for clearer spectral decomposition.
Key Definitions and Concepts
The Jordan Normal Form decomposes a linear operator into generalized eigenspaces, representing it as a block diagonal matrix with Jordan blocks that capture eigenvalues and their algebraic and geometric multiplicities. The Spectral Theorem applies to normal operators on complex inner product spaces, ensuring diagonalization via an orthonormal basis of eigenvectors and associating operators with their spectral measures. Key concepts include eigenvalues, eigenvectors, generalized eigenvectors for Jordan form, and normality, diagonalizability, and spectral measures for the spectral theorem.
Types of Matrices: Applicability and Scope
The Jordan Normal Form applies primarily to square matrices over an algebraically closed field, such as complex matrices, enabling a canonical form even for non-diagonalizable matrices by incorporating Jordan blocks. The Spectral Theorem is specifically applicable to normal matrices, including symmetric, Hermitian, or unitary matrices, guaranteeing diagonalization via orthonormal eigenvectors and real or complex eigenvalues. While Jordan Normal Form offers a detailed classification for general square matrices, the Spectral Theorem provides a more restrictive but highly structured decomposition for matrices with special symmetry properties.
Algebraic vs Geometric Multiplicities
The Jordan Normal Form provides a block matrix representation of a linear operator, highlighting the difference between algebraic and geometric multiplicities through the sizes of Jordan blocks. The spectral theorem applies to normal operators, guaranteeing diagonalization where algebraic and geometric multiplicities coincide, ensuring a basis of eigenvectors. Understanding these multiplicities is crucial: algebraic multiplicity counts eigenvalue occurrences in the characteristic polynomial, while geometric multiplicity measures the dimension of the eigenspace, influencing the matrix's canonical structure.
Diagonalization: When and How
Jordan Normal Form provides a comprehensive framework for diagonalizing linear operators by decomposing them into Jordan blocks when eigenvalues have insufficient eigenvectors, enabling a near-diagonal matrix representation. The Spectral Theorem guarantees diagonalization via orthonormal eigenbases exclusively for normal operators on complex inner product spaces, ensuring a diagonal matrix with orthogonal similarity transformations. Diagonalization occurs under the Spectral Theorem when the operator is normal, while the Jordan Normal Form applies more broadly, allowing canonical forms even for non-diagonalizable matrices.
Real vs Complex Matrices
The Jordan Normal Form provides a canonical representation for complex matrices, allowing for detailed analysis of eigenvalues and their algebraic multiplicities, even when eigenvalues are complex or the matrix is not diagonalizable. The Spectral Theorem applies primarily to real symmetric or complex Hermitian matrices, guaranteeing diagonalization via an orthonormal basis with all eigenvalues real. For real matrices that are not symmetric, the Jordan Normal Form reveals the structure beyond the Spectral Theorem's scope, while the Spectral Theorem offers stability and orthogonality properties critical in applications involving real symmetric or normal operators.
Structure of Jordan Normal Form
The Jordan Normal Form reveals the internal structure of a linear operator by grouping eigenvalues into Jordan blocks, each corresponding to an eigenvalue and its generalized eigenspace. This form highlights the presence of non-diagonalizable components through the size and number of Jordan blocks, providing a detailed picture of the operator's nilpotent part. In contrast, the Spectral Theorem applies specifically to normal operators, ensuring a diagonalization with orthonormal eigenvectors but lacking the finer decomposition into Jordan blocks for defective eigenvalues.
Properties of the Spectral Theorem
The spectral theorem guarantees that any normal matrix over the complex field is unitarily diagonalizable, providing a basis of eigenvectors that are orthonormal. It ensures the matrix can be expressed as a sum of projections scaled by eigenvalues, revealing a clear geometric structure. Unlike the Jordan normal form, which may involve Jordan blocks for non-diagonalizable matrices, the spectral theorem applies strictly to normal operators, offering a more straightforward diagonalization with real or complex eigenvalues.
Practical Applications and Examples
Jordan Normal Form is essential in solving systems of linear differential equations and analyzing linear transformations with defective eigenvalues, particularly in control theory and vibrations analysis. The Spectral Theorem provides a practical framework for diagonalizing normal operators, widely used in quantum mechanics and signal processing for simplifying matrix computations. Both tools enable advanced matrix decompositions, but Jordan Normal Form handles non-diagonalizable matrices while the Spectral Theorem applies to symmetric or normal matrices for real eigenvalue decompositions.
Summary: Choosing the Right Tool
Jordan Normal Form excels in addressing linear operators with defective eigenvalues and provides a detailed algebraic structure through Jordan blocks. The Spectral Theorem applies specifically to normal operators, guaranteeing diagonalization via an orthonormal basis and enabling easier interpretation of operator behavior. Selecting between these depends on matrix properties: use the Jordan Normal Form for general matrices with possible non-diagonalizability and the Spectral Theorem for normal matrices assuring orthogonal diagonalization.
Jordan Normal Form Infographic
 libterm.com
libterm.com