An unconditional basis in mathematics refers to a type of basis in a Banach space where convergence of series does not depend on the order of terms, ensuring stability and robustness in representation. This property is crucial for various applications in functional analysis and signal processing, as it guarantees that rearranging or modifying coefficients won't affect the outcome. Explore the rest of the article to understand how unconditional bases impact your work in analysis and applied mathematics.
Table of Comparison
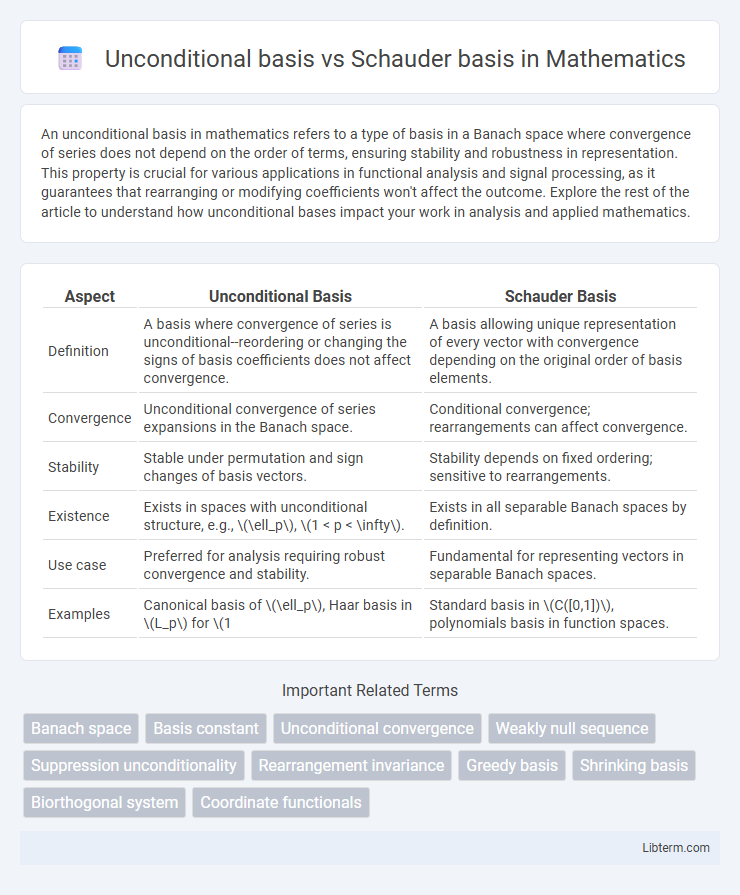
| Aspect | Unconditional Basis | Schauder Basis |
|---|---|---|
| Definition | A basis where convergence of series is unconditional--reordering or changing the signs of basis coefficients does not affect convergence. | A basis allowing unique representation of every vector with convergence depending on the original order of basis elements. |
| Convergence | Unconditional convergence of series expansions in the Banach space. | Conditional convergence; rearrangements can affect convergence. |
| Stability | Stable under permutation and sign changes of basis vectors. | Stability depends on fixed ordering; sensitive to rearrangements. |
| Existence | Exists in spaces with unconditional structure, e.g., \(\ell_p\), \(1 < p < \infty\). | Exists in all separable Banach spaces by definition. |
| Use case | Preferred for analysis requiring robust convergence and stability. | Fundamental for representing vectors in separable Banach spaces. |
| Examples | Canonical basis of \(\ell_p\), Haar basis in \(L_p\) for \(1| Standard basis in \(C([0,1])\), polynomials basis in function spaces. |
|
Introduction to Bases in Functional Analysis
Unconditional bases in functional analysis allow series expansions of elements in a Banach space to converge regardless of the order of terms, enhancing stability in approximations. Schauder bases, however, require convergence only in the original order, providing a foundational yet order-dependent tool for representing vectors. Understanding the distinction between unconditional and Schauder bases is crucial for analyzing the structural properties of Banach spaces and their applications in operator theory and signal processing.
Defining Schauder Basis
A Schauder basis in a Banach space is a sequence \( (x_n) \) such that every element in the space can be uniquely represented as a convergent series of scalars times these basis elements, ensuring strong topological control. Unlike an unconditional basis, where convergence of the series is independent of the order of terms, a Schauder basis only guarantees convergence in the original order, highlighting its reliance on the linear topological structure. The distinction between unconditional and Schauder bases is critical in functional analysis, impacting the study of normed vector spaces and approximation theory.
Understanding Unconditional Basis
An unconditional basis allows series expansions to converge regardless of the order of terms, contrasting with Schauder bases where convergence depends on a fixed sequence. This property ensures stability and robustness in functional analysis and signal processing applications. Understanding unconditional bases is crucial for working with Banach spaces and improving algorithms in numerical analysis.
Key Differences between Unconditional and Schauder Bases
Unconditional bases allow series expansions of vectors to converge regardless of the order of summation, while Schauder bases require convergence in a specific order, ensuring unique representation of vectors in Banach spaces. In an unconditional basis, rearrangements of terms do not affect convergence, providing greater flexibility in analysis and applications. Conversely, Schauder bases offer a well-defined expansion but lack this robustness to reorderings, making unconditional bases a stronger structural property.
Examples of Schauder Basis in Classic Banach Spaces
The canonical example of a Schauder basis is the sequence of unit vectors in the Banach space l^p for 1 <= p < , where every element can be uniquely expressed as a convergent series of these vectors, demonstrating the space's separability. Another classical Schauder basis is the Haar system in L^p([0,1]) for 1 < p < , which provides an orthonormal basis in L^2([0,1]) and a conditional basis for other p-values. The trigonometric system forms a Schauder basis in certain subspaces of continuous functions on the circle, illustrating the broad applicability of Schauder bases beyond sequence spaces.
Properties and Applications of Unconditional Bases
Unconditional bases allow series expansions in Banach spaces to converge regardless of term order, providing stability and flexibility crucial for functional analysis and signal processing. Their key properties include unconditional convergence, uniform boundedness of coordinate functionals, and robustness under perturbations, which make them essential in approximation theory and numerical methods. Applications span wavelet decompositions, compressed sensing, and solving differential equations, where independence from term rearrangement enhances computational efficiency and accuracy.
Criteria for a Basis to be Schauder or Unconditional
A Schauder basis requires every element in a Banach space to be uniquely representable as a norm-convergent series of basis vectors with continuous coordinate functionals, ensuring stability under linear combinations. An unconditional basis further demands convergence of the series representing each element regardless of the order or signs of the coefficients, characterized by the unconditional constant controlling the norm of projections. The key criterion for a basis to be unconditional is that all permutations of the series converge to the same limit, while Schauder bases only guarantee convergence for the natural ordering.
Importance of Unconditional Basis in Infinite-Dimensional Spaces
Unconditional bases are crucial in infinite-dimensional spaces because they allow series expansions to converge regardless of the order of terms, ensuring stability and robustness in functional analysis and Banach space theory. Unlike Schauder bases, which require a fixed order for convergence, unconditional bases enable rearrangements without affecting the limit, facilitating simpler operator theory and decomposition techniques. This property is essential for applications in signal processing, numerical analysis, and the study of linear operators on infinite-dimensional spaces.
Implications for Series Convergence and Stability
Unconditional bases guarantee that series convergence is independent of the order of terms, ensuring absolute convergence and robust stability under rearrangements, which is critical in functional analysis and signal processing. Schauder bases, while providing unique representations for elements in Banach spaces, only ensure conditional convergence, making the series sensitive to term permutation and potentially affecting numerical stability. The distinction impacts the design of algorithms in applied mathematics where unconditional bases enhance convergence reliability, whereas Schauder bases require careful handling to maintain series stability.
Conclusion: Choosing the Right Basis for Analysis
Choosing between an unconditional basis and a Schauder basis depends on the specific analytical goals and the nature of the Banach space in question. Unconditional bases provide greater flexibility and stability in expansions, allowing rearrangements without affecting convergence, which is crucial for applications requiring robustness under manipulation. Schauder bases, while less restrictive, are easier to construct and suffice for many practical problems where order and convergence control are not as critical.
Unconditional basis Infographic
 libterm.com
libterm.com