A supermartingale is a type of stochastic process used in probability theory and financial mathematics, where the expected value of the next observation is always less than or equal to the current value, reflecting a non-increasing trend over time. This concept is crucial in modeling scenarios involving decreasing asset prices or risk management strategies like betting systems. Explore the rest of the article to understand how supermartingales apply to your financial decisions and risk assessments.
Table of Comparison
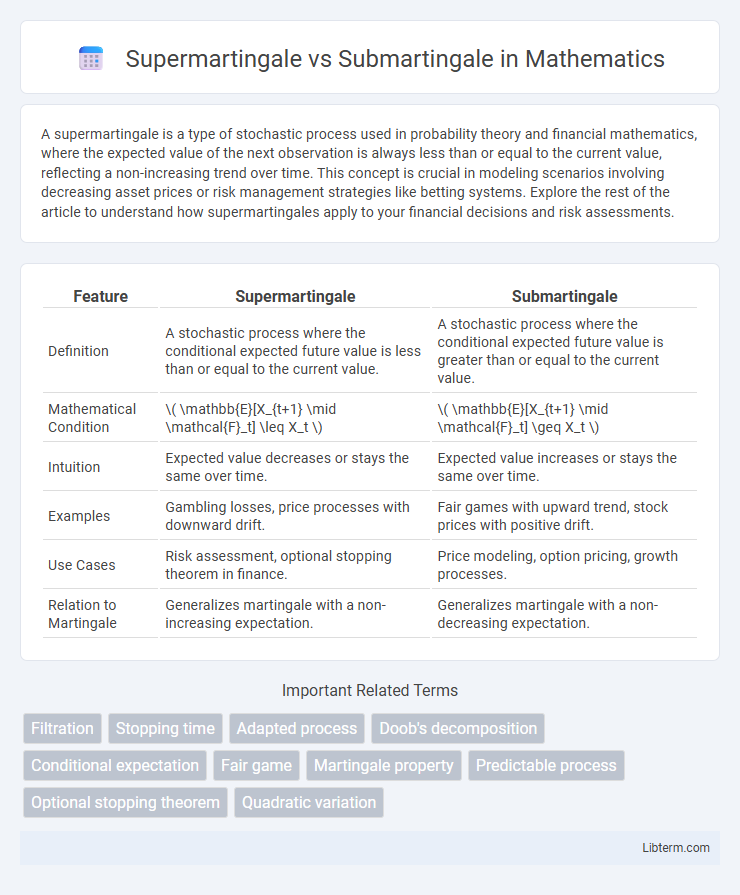
| Feature | Supermartingale | Submartingale |
|---|---|---|
| Definition | A stochastic process where the conditional expected future value is less than or equal to the current value. | A stochastic process where the conditional expected future value is greater than or equal to the current value. |
| Mathematical Condition | \( \mathbb{E}[X_{t+1} \mid \mathcal{F}_t] \leq X_t \) | \( \mathbb{E}[X_{t+1} \mid \mathcal{F}_t] \geq X_t \) |
| Intuition | Expected value decreases or stays the same over time. | Expected value increases or stays the same over time. |
| Examples | Gambling losses, price processes with downward drift. | Fair games with upward trend, stock prices with positive drift. |
| Use Cases | Risk assessment, optional stopping theorem in finance. | Price modeling, option pricing, growth processes. |
| Relation to Martingale | Generalizes martingale with a non-increasing expectation. | Generalizes martingale with a non-decreasing expectation. |
Introduction to Martingales
A supermartingale is a stochastic process where the conditional expected value of the next observation, given all past observations, is less than or equal to the present value, reflecting a tendency to decrease or stay the same over time. In contrast, a submartingale exhibits a conditional expected value that is greater than or equal to the current observation, indicating a non-decreasing trend in expectation. Both supermartingales and submartingales are specialized forms of martingales, which have constant conditional expectations and serve as fundamental models in probability theory and financial mathematics for modeling fair games and asset price behaviors.
Defining Supermartingales
Supermartingales are stochastic processes where the conditional expectation of the next value, given all past values, is less than or equal to the current value, reflecting a non-increasing trend over time. This contrasts with submartingales, which demonstrate a non-decreasing conditional expectation, indicating potential growth. Supermartingales play a crucial role in probability theory and financial modeling, particularly in understanding strategies involving decreasing expected returns.
Understanding Submartingales
Submartingales represent stochastic processes where the expected future value, conditioned on the present and past, is at least as large as the current value, indicating a non-decreasing trend on average. This property makes submartingales essential in modeling scenarios with a tendency for growth or accumulation, such as certain financial asset prices or accumulative betting strategies. Understanding submartingales involves grasping their use in probability theory and stochastic analysis, where they contrast with supermartingales that exhibit non-increasing expected values over time.
Key Differences: Supermartingale vs Submartingale
Supermartingales and submartingales differ primarily in their conditional expectation properties: a supermartingale has a conditional expected value less than or equal to the current value, reflecting a non-increasing trend, while a submartingale's conditional expected value is greater than or equal to the current value, indicating a non-decreasing trend. In stochastic processes, supermartingales model scenarios where the expected future value tends to decrease or remain the same, often used in risk assessments, whereas submartingales model processes with an expected increase or stability, common in financial modeling for asset prices. Understanding these distinctions is critical for applications in probability theory, particularly in martingale convergence theorems and optimal stopping problems.
Mathematical Properties and Conditions
Supermartingale and submartingale are types of stochastic processes characterized by their conditional expectations; a supermartingale \( (X_t) \) satisfies \( \mathbb{E}[X_{t+1}|\mathcal{F}_t] \leq X_t \) almost surely, indicating a non-increasing trend in expectation, while a submartingale satisfies \( \mathbb{E}[X_{t+1}|\mathcal{F}_t] \geq X_t \), reflecting a non-decreasing trend. Both processes are adapted to a filtration \( (\mathcal{F}_t) \) and require integrability conditions such as \( \mathbb{E}[|X_t|] < \infty \) for all \( t \), ensuring well-defined conditional expectations. Key mathematical properties include the optional stopping theorem and convergence theorems, which hold under appropriate conditions, such as boundedness or uniform integrability, making supermartingales useful in modeling systems with expected losses and submartingales in settings with expected gains.
Practical Examples in Probability Theory
A supermartingale is a stochastic process where the expected future value is always less than or equal to the current value, exemplified by a fair game with a losing bias, such as a gambler's bankroll in a casino with a house edge. A submartingale, conversely, has an expected future value greater than or equal to its current value, often modeled by an investor's wealth in a favorable market with expected positive returns. These concepts are crucial in probability theory for modeling scenarios like stock prices, risk assessment, and optimal stopping problems, where anticipating the direction of the expected value guides decision-making.
Applications in Finance and Economics
Supermartingales and submartingales are crucial in modeling asset prices and risk processes in finance and economics. Submartingales represent fair game processes with an expected upward trend, useful in option pricing and investment strategies forecasting gains, whereas supermartingales model asset price processes with an expected downward trend, helping to assess risk and potential losses. Their properties underpin the fundamental theorem of asset pricing and optimal stopping theory, enabling dynamic portfolio optimization and risk management.
Common Misconceptions Explained
Supermartingales are stochastic processes where the expected future value is less than or equal to the present value, while submartingales have expected future values greater than or equal to the present value. A common misconception is that supermartingales always decrease and submartingales always increase, but both can fluctuate over time depending on the underlying random variables. Understanding these nuances is crucial in fields like financial mathematics and stochastic analysis, where these processes model fair games and price movements.
Advantages and Limitations of Each Process
Supermartingales offer the advantage of modeling processes with a decreasing or fair expected value, making them ideal for risk-averse scenarios and conservative betting strategies. Submartingales excel in representing processes with non-decreasing expected values, useful in growth modeling and investment analysis, but they may overestimate future gains under volatile conditions. Limitations of supermartingales include potential underestimation of upward trends, while submartingales can lead to biased expectations in declining environments, requiring careful context-specific application.
Summary and Final Thoughts on Martingale Processes
Supermartingales represent stochastic processes where the expected future value is less than or equal to the present value, often modeling declining trends or losses. Submartingales exhibit the opposite behavior, with expected future values greater than or equal to current values, reflecting potential gains or increasing trends. Both supermartingales and submartingales serve as fundamental constructs in probability theory, underpinning risk assessment, financial modeling, and optimal stopping problems by capturing essential directional tendencies in martingale processes.
Supermartingale Infographic
 libterm.com
libterm.com