Stereographic projection transforms points from a sphere onto a plane, preserving angles and shapes locally, making it essential for complex analysis and cartography. This method is widely used in visualizing globe features on flat maps without distortions of small shapes. Explore the rest of the article to understand how stereographic projection benefits your spatial understanding and mathematical applications.
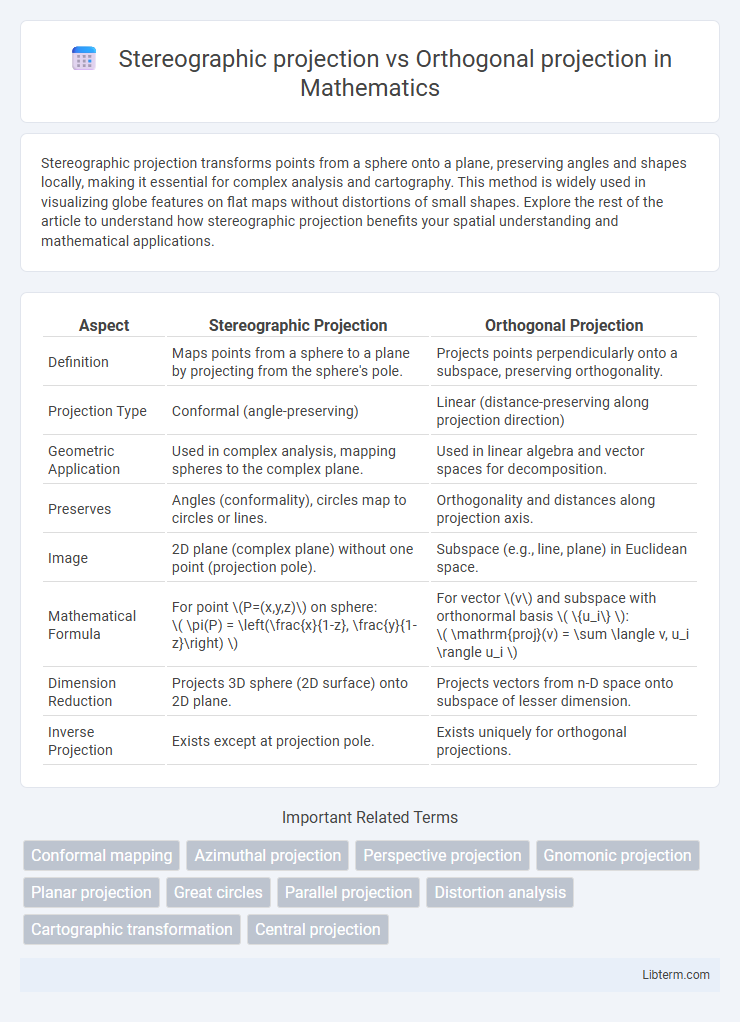
Table of Comparison
| Aspect | Stereographic Projection | Orthogonal Projection |
|---|---|---|
| Definition | Maps points from a sphere to a plane by projecting from the sphere's pole. | Projects points perpendicularly onto a subspace, preserving orthogonality. |
| Projection Type | Conformal (angle-preserving) | Linear (distance-preserving along projection direction) |
| Geometric Application | Used in complex analysis, mapping spheres to the complex plane. | Used in linear algebra and vector spaces for decomposition. |
| Preserves | Angles (conformality), circles map to circles or lines. | Orthogonality and distances along projection axis. |
| Image | 2D plane (complex plane) without one point (projection pole). | Subspace (e.g., line, plane) in Euclidean space. |
| Mathematical Formula |
For point \(P=(x,y,z)\) on sphere: \( \pi(P) = \left(\frac{x}{1-z}, \frac{y}{1-z}\right) \) |
For vector \(v\) and subspace with orthonormal basis \( \{u_i\} \): \( \mathrm{proj}(v) = \sum \langle v, u_i \rangle u_i \) |
| Dimension Reduction | Projects 3D sphere (2D surface) onto 2D plane. | Projects vectors from n-D space onto subspace of lesser dimension. |
| Inverse Projection | Exists except at projection pole. | Exists uniquely for orthogonal projections. |
Introduction to Projection Methods
Stereographic projection maps points from a sphere onto a plane by projecting through the sphere's opposite pole, preserving angles and shapes locally, making it crucial in complex analysis and cartography. Orthogonal projection involves dropping perpendiculars from points onto a plane, preserving distances along projection lines, commonly used in engineering and architectural drawing for accurate dimensional representation. Both projection methods serve distinct purposes in geometry and visualization by balancing shape, angle, and distance preservation based on application needs.
Overview of Stereographic Projection
Stereographic projection is a conformal mapping technique that projects points from a sphere onto a plane, preserving angles but not areas or distances. It is widely used in cartography, complex analysis, and crystallography for representing spherical surfaces while maintaining local shapes. Unlike orthogonal projection, which projects points perpendicularly onto a plane preserving distances along certain axes, stereographic projection provides a one-to-one correspondence with the sphere minus the projection point.
Fundamentals of Orthogonal Projection
Orthogonal projection maps points perpendicularly onto a plane, preserving angles and distances along projection lines, making it essential in engineering and architectural drawings for accurate measurements. Unlike stereographic projection, which projects points from a sphere onto a plane through a point on the sphere, orthogonal projection maintains true scale and shape along coordinate axes. The fundamentals of orthogonal projection rely on projecting vectors onto subspaces using dot products and linear algebra to achieve precise planar representations of three-dimensional objects.
Mathematical Principles Behind Each Projection
Stereographic projection maps points from a sphere onto a plane using lines drawn from the sphere's opposite pole, preserving angles and conformal properties through a rational function with complex analysis foundations. Orthogonal projection involves projecting points perpendicularly onto a plane, minimizing distortion in distances along the projection axis while sacrificing angle preservation, grounded in linear algebra and Euclidean geometry. The mathematical principles distinguish stereographic projection's conformality from orthogonal projection's simplicity and directness in preserving spatial relationships along a normal vector.
Visual Representation and Geometric Differences
Stereographic projection maps a sphere onto a plane by projecting points from the sphere through the North Pole, preserving angles but distorting areas, resulting in circular arcs representing great circles. Orthogonal projection translates three-dimensional objects directly onto a plane using perpendicular rays, preserving true proportions and distances along the projection axes but distorting shapes depending on the object's orientation. The geometric difference lies in stereographic's conformal nature maintaining angular relationships versus orthogonal's metric preservation emphasizing accurate measurements without preserving angles.
Applications of Stereographic Projection
Stereographic projection is widely used in cartography for mapping spherical surfaces onto a plane, preserving angles and shapes of small objects, making it ideal for applications in geology and crystallography. This projection technique is essential in complex analysis for visualizing the Riemann sphere, and in computer graphics for panoramic imaging and texture mapping due to its conformal properties. Unlike orthogonal projection, which maintains true scale along axes but distorts angles, stereographic projection excels in applications requiring angle preservation and smooth mapping of curved surfaces.
Practical Uses of Orthogonal Projection
Orthogonal projection is widely used in engineering and architectural design for creating accurate and measurable 2D representations of 3D objects, enabling precise dimensioning and technical drawing. It is essential in computer graphics and CAD software for rendering objects without perspective distortion, facilitating detailed analysis and modifications. Unlike stereographic projection, orthogonal projection maintains true scale and angles, making it indispensable for manufacturing and construction processes.
Advantages and Limitations Compared
Stereographic projection excels in representing complex geometric shapes on a two-dimensional plane with conformal properties, preserving angles and shapes locally, making it ideal for cartography and complex analysis, but it introduces distortion in area and scale especially near projection poles. Orthogonal projection maintains true dimensions along axes and is simpler for technical and engineering drawings, enabling precise measurements and straightforward visualization, yet it fails to preserve angles and can distort shapes significantly. Choosing between stereographic and orthogonal projections depends on whether preserving shape fidelity or dimensional accuracy is prioritized in applications like map-making, architectural design, and data visualization.
Choosing the Right Projection Method
Selecting the appropriate projection method depends on the application's goals and the nature of the data; stereographic projection excels in preserving angles, making it ideal for conformal mapping in complex analysis and cartography. Orthogonal projection maintains true scale along axes, which is critical for engineering designs and architectural plans where accurate measurements are essential. Understanding the geometric properties and distortion characteristics of stereographic and orthogonal projections enables optimal decision-making for accurate spatial representation.
Conclusion and Future Perspectives
Stereographic projection preserves angles and is conformal, making it ideal for applications in complex analysis and cartography where local shape fidelity is crucial, while orthogonal projection maintains true scale along axes, benefiting engineering and architectural designs requiring accurate measurements. Future advancements in computational geometry may integrate hybrid models combining stereographic projection's angular accuracy with orthogonal projections' dimensional fidelity to optimize visualization and data representation. Emerging technologies in augmented reality and 3D mapping will likely leverage these projections to enhance spatial understanding and precision in virtual environments.
Stereographic projection Infographic
 libterm.com
libterm.com