Convergence in measure occurs when the measure of the set where a sequence of functions differs from a limiting function by more than a given positive number approaches zero. This concept is crucial in real analysis and probability theory for understanding function behavior without requiring pointwise convergence. Explore the rest of the article to deepen your understanding of convergence in measure and its applications.
Table of Comparison
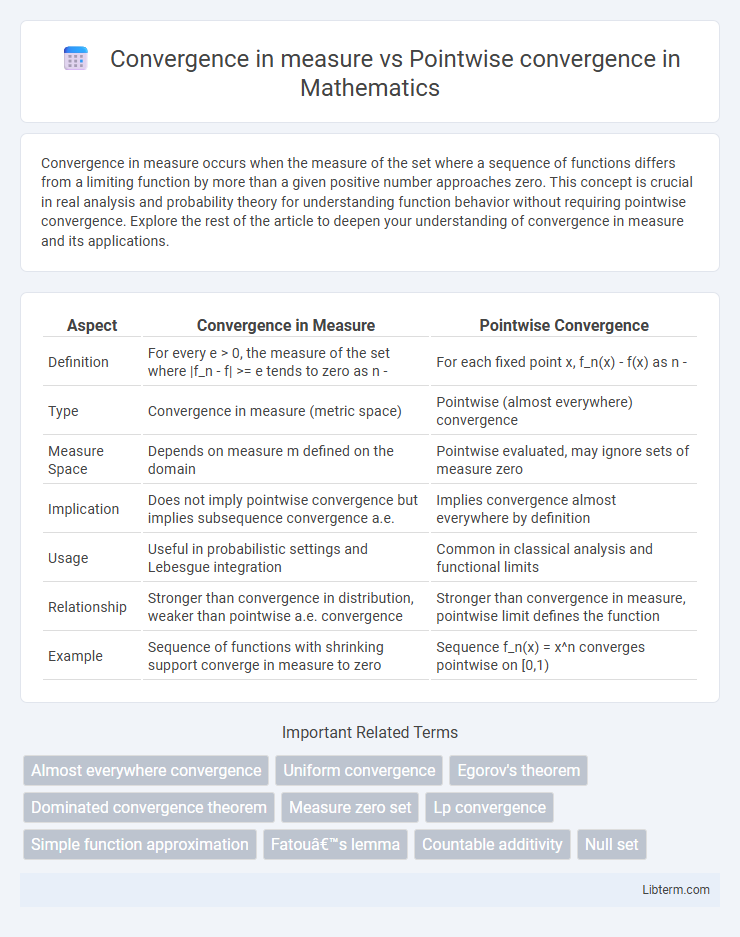
| Aspect | Convergence in Measure | Pointwise Convergence |
|---|---|---|
| Definition | For every e > 0, the measure of the set where |f_n - f| >= e tends to zero as n - | For each fixed point x, f_n(x) - f(x) as n - |
| Type | Convergence in measure (metric space) | Pointwise (almost everywhere) convergence |
| Measure Space | Depends on measure m defined on the domain | Pointwise evaluated, may ignore sets of measure zero |
| Implication | Does not imply pointwise convergence but implies subsequence convergence a.e. | Implies convergence almost everywhere by definition |
| Usage | Useful in probabilistic settings and Lebesgue integration | Common in classical analysis and functional limits |
| Relationship | Stronger than convergence in distribution, weaker than pointwise a.e. convergence | Stronger than convergence in measure, pointwise limit defines the function |
| Example | Sequence of functions with shrinking support converge in measure to zero | Sequence f_n(x) = x^n converges pointwise on [0,1) |
Introduction to Convergence in Analysis
Convergence in measure and pointwise convergence are fundamental concepts in real analysis that describe different modes by which sequences of functions approach a limiting function. Pointwise convergence requires that for each fixed point in the domain, the sequence of function values converges to the limiting function value, while convergence in measure allows for exceptions on sets with arbitrarily small measure, offering a more flexible framework particularly useful in measure theory and integration. Understanding these convergence types is essential in analyzing function behavior in L^p spaces and Lebesgue integration.
Defining Pointwise Convergence
Pointwise convergence of a sequence of functions \((f_n)\) to a function \(f\) occurs when, for every point \(x\) in the domain, the sequence \((f_n(x))\) converges to \(f(x)\) as \(n \to \infty\). This type of convergence is defined by evaluating limits independently at each point, emphasizing local behavior rather than global or measure-theoretic properties. Unlike convergence in measure, pointwise convergence does not require the functions to be close on a large subset of the domain, only at each individual point.
Understanding Convergence in Measure
Convergence in measure occurs when the measure of the set where functions differ from the limit by at least a given e approaches zero, making it a probabilistic form of convergence useful in measure theory and probability. Unlike pointwise convergence, which requires each point to converge individually, convergence in measure allows for exceptions on small sets of diminishing measure. This concept is crucial in spaces like L^p, where pointwise convergence may fail but convergence in measure still guarantees meaningful limits for sequences of measurable functions.
Key Differences Between Pointwise and Measure Convergence
Pointwise convergence occurs when a sequence of functions converges at each individual point, requiring the limit to hold for every point in the domain, while convergence in measure involves the measure of the set where the functions differ from the limit by more than a given epsilon tending to zero. Pointwise convergence is a stronger notion, ensuring function values get arbitrarily close at each point, whereas convergence in measure allows discrepancies on sets of vanishing measure. In measure theory, convergence in measure is often preferred due to its flexibility in handling functions equal almost everywhere, contrasting with the stricter pointwise convergence that demands uniform behavior across the domain.
Examples Illustrating Pointwise Convergence
Pointwise convergence occurs when a sequence of functions f_n converges to a function f at each individual point in the domain, such as f_n(x) = x^n on [0,1), which converges pointwise to the function f(x) that is 0 for x in [0,1) and 1 at x=1. Another example is the sequence f_n(x) = sin(x)/n, which converges pointwise to the zero function as n approaches infinity for all real x. These examples highlight how pointwise convergence differs from convergence in measure by focusing on individual points rather than measure-theoretic properties of the sequence.
Examples Demonstrating Convergence in Measure
Convergence in measure occurs when for any e > 0, the measure of the set where functions differ from the limit by more than e tends to zero, exemplified by the sequence f_n(x) = x^n on [0,1], which converges in measure to the function that is zero on [0,1) and one at x=1, despite not converging pointwise everywhere. Another example involves indicator functions f_n(x) = 1_{[0,1/n]}(x) on [0,1], converging in measure to the zero function, while pointwise convergence holds only almost everywhere except at zero. Such examples illustrate that convergence in measure does not imply pointwise convergence, highlighting distinct modes of function convergence in measure theory.
Implications for Function Sequences
Convergence in measure for function sequences ensures that the measure of the set where functions differ significantly from the limit function approaches zero, making it suitable for integration and probability contexts. Pointwise convergence requires each point to converge individually, which does not guarantee integrability or uniform behavior over the domain. Sequences converging in measure may lack pointwise convergence but still provide strong results in L^p spaces and are essential in real analysis and measure theory.
Relationships Between the Two Types of Convergence
Convergence in measure implies pointwise convergence of a subsequence almost everywhere, while pointwise convergence does not necessarily guarantee convergence in measure. If a sequence of measurable functions converges pointwise almost everywhere to a function on a finite measure space, then it also converges in measure to that function. Convergence in measure emphasizes the size of the set where functions differ significantly, whereas pointwise convergence focuses on behavior at individual points.
Common Misconceptions and Pitfalls
Convergence in measure does not imply pointwise convergence, as sequences can converge in measure without converging at every point, leading to common misconceptions that confuse these two modes of convergence. A frequent pitfall is assuming that pointwise convergence follows from convergence in measure, ignoring that convergence in measure only guarantees convergence on a set of large measure, not necessarily on individual points. Understanding that convergence in measure deals with the "size" of the set where functions differ significantly, while pointwise convergence focuses on behavior at each point, is crucial to avoid these misunderstandings.
Applications in Real Analysis and Probability Theory
Convergence in measure is crucial in real analysis for handling functions that do not converge pointwise but still exhibit strong integrability properties, making it essential in the study of Lebesgue integration and spaces like L^p. Pointwise convergence, while more intuitive, is less robust in probabilistic settings but important in establishing almost sure convergence of random variables, which underpins limit theorems such as the Strong Law of Large Numbers. Both modes of convergence play complementary roles in probability theory: convergence in measure corresponds to convergence in probability, facilitating the analysis of stochastic processes, whereas pointwise convergence relates to sample path properties of random functions.
Convergence in measure Infographic
 libterm.com
libterm.com