A principal bundle is a mathematical structure that formalizes the concept of a space equipped with a group action acting freely and transitively on its fibers, commonly used in geometry and topology to study fiber bundles with a group symmetry. It plays a crucial role in gauge theory, allowing the formulation of connections, curvature, and holonomy in a rigorous way. Discover how principal bundles underpin advanced mathematical frameworks and their applications in physics by reading the rest of the article.
Table of Comparison
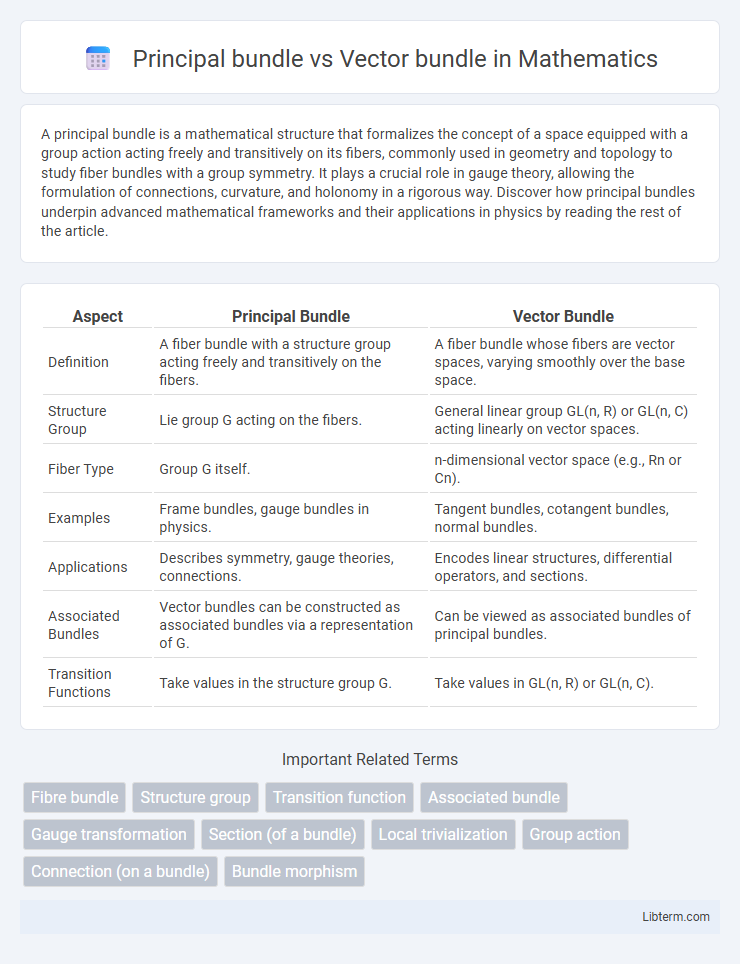
| Aspect | Principal Bundle | Vector Bundle |
|---|---|---|
| Definition | A fiber bundle with a structure group acting freely and transitively on the fibers. | A fiber bundle whose fibers are vector spaces, varying smoothly over the base space. |
| Structure Group | Lie group G acting on the fibers. | General linear group GL(n, R) or GL(n, C) acting linearly on vector spaces. |
| Fiber Type | Group G itself. | n-dimensional vector space (e.g., Rn or Cn). |
| Examples | Frame bundles, gauge bundles in physics. | Tangent bundles, cotangent bundles, normal bundles. |
| Applications | Describes symmetry, gauge theories, connections. | Encodes linear structures, differential operators, and sections. |
| Associated Bundles | Vector bundles can be constructed as associated bundles via a representation of G. | Can be viewed as associated bundles of principal bundles. |
| Transition Functions | Take values in the structure group G. | Take values in GL(n, R) or GL(n, C). |
Introduction to Bundles in Differential Geometry
Principal bundles and vector bundles are fundamental concepts in differential geometry, serving as structured fiber bundles that facilitate the study of manifolds and their symmetries. A principal bundle has a Lie group as its typical fiber and governs symmetry transformations, while a vector bundle features vector spaces as fibers, enabling linear algebraic techniques on manifolds. Understanding the distinction between these bundles is essential for exploring gauge theories, connections, and curvature in geometric contexts.
Defining Principal Bundles
Principal bundles are defined by a total space equipped with a free and transitive right action of a Lie group G, projecting onto a base manifold such that locally the bundle resembles the product of the base with G. This structure contrasts with vector bundles, which have fibers modeled on vector spaces and feature linear transition functions. The defining characteristic of principal bundles lies in the smooth, group-equivariant projection and the ability to frame associated bundles using representation of G.
Defining Vector Bundles
Vector bundles consist of a family of vector spaces parametrized continuously by a topological space, where each fiber is a vector space and local trivializations preserve linear structure. The defining feature of vector bundles is their transition functions, which take values in the general linear group GL(n, R) reflecting linear isomorphisms between fibers. Principal bundles generalize this concept, focusing on a structure group acting freely and transitively on fibers, but do not themselves carry a vector space structure like vector bundles.
Structure Groups: Comparison and Contrast
Principal bundles feature structure groups that act freely and transitively on the fiber, serving as the framework for the bundle's symmetry, often represented by Lie groups like GL(n) or O(n). Vector bundles have structure groups derived from linear transformations preserving vector space structures, typically subgroups of GL(n), with fibers modeled as vector spaces enabling linear algebraic operations. The primary contrast lies in how principal bundles emphasize group actions abstractly while vector bundles impose linear structures, making principal bundles the foundation for constructing associated vector bundles via their structure groups.
Local Trivialization in Principal and Vector Bundles
Local trivialization in principal bundles involves representing the bundle as a product of an open set in the base space and the structure group, allowing the bundle to appear locally as \( U \times G \) with transition functions given by group multiplication. In vector bundles, local trivialization expresses the bundle locally as \( U \times \mathbb{R}^n \), where the fibers are vector spaces and transition functions are linear isomorphisms between fibers. While principal bundles use the group action for transition maps, vector bundles rely on linear transformations preserving vector space structure during local trivializations.
Transition Functions and Their Roles
Transition functions in principal bundles are maps valued in the structure group that specify how local trivializations relate, encoding the bundle's symmetry and enabling the construction of the bundle from local data via cocycle conditions. In vector bundles, transition functions are represented by invertible linear transformations (GL(n)-valued functions) defining how vector spaces on overlapping charts relate, ensuring consistency of the vector space structure. The role of transition functions is crucial for defining the bundle's topology and geometry, with principal bundles emphasizing group actions and vector bundles focusing on linear structure compatibility.
Morphisms between Bundles
Morphisms between principal bundles are bundle maps that preserve the group action, equivariantly intertwining the structure groups of the bundles involved. In contrast, morphisms between vector bundles are linear bundle maps respecting the vector space structure on each fiber. These morphism constraints ensure that principal bundles maintain their G-torsor properties, while vector bundle morphisms preserve linearity and fiberwise vector space operations.
Associated Bundles: Linking Principal and Vector Bundles
Associated bundles serve as a fundamental bridge between principal bundles and vector bundles by constructing a vector bundle from a principal G-bundle via a representation of the structure group G on a vector space V. This construction assigns to each point in the base manifold a vector space that transforms according to the representation, effectively allowing the geometry and symmetry encoded in the principal bundle to influence the fiber structure of the vector bundle. The resulting associated vector bundle captures the action of the Lie group on both the principal and vector bundles, providing a rich framework for studying gauge theories, fiber bundle classification, and differential geometry.
Applications of Principal and Vector Bundles
Principal bundles are fundamental in gauge theory and the study of fiber bundles with a Lie group as the structure group, playing a crucial role in mathematical physics by modeling fields and connections in gauge theories. Vector bundles are widely used in differential geometry and topology to study sections, such as vector fields and differential forms, providing a natural framework for linear algebraic structures on manifolds. Both bundles enable the formulation of complex geometric and physical problems, but principal bundles emphasize symmetry and group actions, while vector bundles focus on linear structures and fields.
Key Differences and Summary
Principal bundles are fiber bundles with a Lie group as the fiber, acting freely and transitively on itself, essential in gauge theory and defining connections. Vector bundles, by contrast, have vector spaces as fibers, equipped with linear structure, commonly used in differential geometry for sections like tangent and normal bundles. The key distinction lies in the fiber's structure and group action: principal bundles emphasize symmetry groups, while vector bundles focus on linear algebraic properties.
Principal bundle Infographic
 libterm.com
libterm.com