Geometric design integrates shapes, lines, and patterns to create visually striking and balanced compositions. Understanding geometric principles enhances your ability to apply symmetry and proportion effectively in art, architecture, and design projects. Explore the rest of this article to uncover practical tips and inspiring examples related to geometric concepts.
Table of Comparison
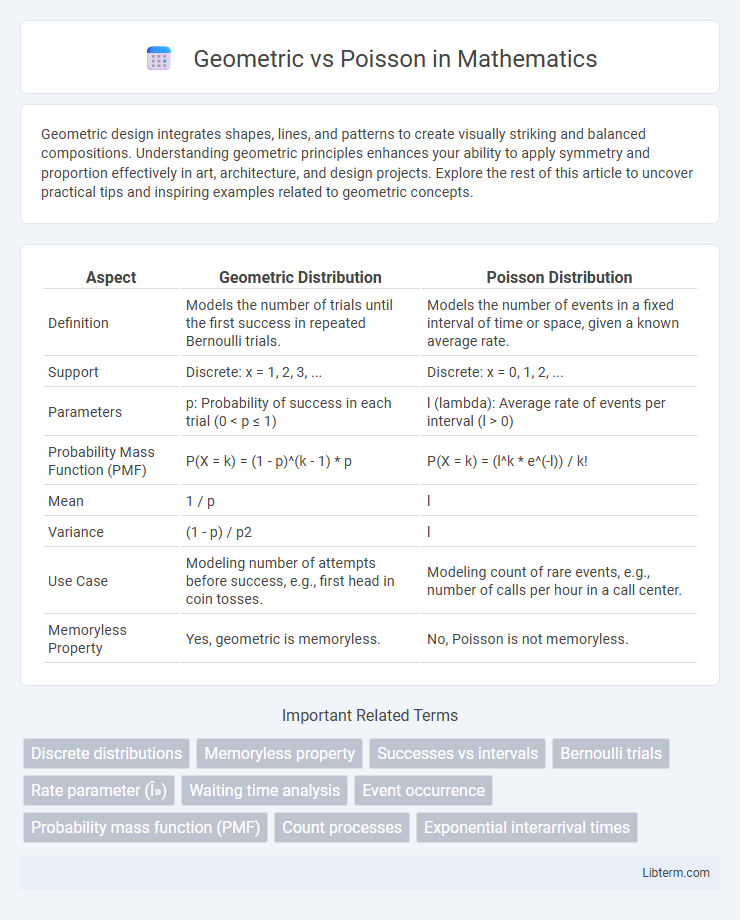
| Aspect | Geometric Distribution | Poisson Distribution |
|---|---|---|
| Definition | Models the number of trials until the first success in repeated Bernoulli trials. | Models the number of events in a fixed interval of time or space, given a known average rate. |
| Support | Discrete: x = 1, 2, 3, ... | Discrete: x = 0, 1, 2, ... |
| Parameters | p: Probability of success in each trial (0 < p ≤ 1) | l (lambda): Average rate of events per interval (l > 0) |
| Probability Mass Function (PMF) | P(X = k) = (1 - p)^(k - 1) * p | P(X = k) = (l^k * e^(-l)) / k! |
| Mean | 1 / p | l |
| Variance | (1 - p) / p2 | l |
| Use Case | Modeling number of attempts before success, e.g., first head in coin tosses. | Modeling count of rare events, e.g., number of calls per hour in a call center. |
| Memoryless Property | Yes, geometric is memoryless. | No, Poisson is not memoryless. |
Introduction to Geometric and Poisson Distributions
Geometric and Poisson distributions are fundamental concepts in probability theory used to model different types of random events. The geometric distribution describes the probability of the first success occurring on the k-th trial in a series of independent Bernoulli trials with success probability p, making it essential in scenarios involving waiting times until the first success. The Poisson distribution models the number of events occurring in a fixed interval of time or space, given the events happen independently at a constant average rate l, widely applied in fields such as telecommunications, traffic flow, and queueing theory.
Key Differences between Geometric and Poisson
The Geometric distribution models the number of trials until the first success in a series of independent Bernoulli trials with constant probability p, whereas the Poisson distribution describes the number of events occurring in a fixed interval of time or space, given a constant average rate l. The Geometric distribution is discrete with support on positive integers starting from 1, while the Poisson distribution takes non-negative integer values starting from 0. Key differences include the memoryless property held by the Geometric distribution and the Poisson distribution's suitability for modeling rare events in continuous time or space.
Mathematical Definitions and Formulations
The Geometric distribution models the number of trials until the first success, defined by the probability mass function P(X = k) = (1 - p)^(k-1) * p for k >= 1, where p is the success probability in each trial. The Poisson distribution describes the number of events occurring in a fixed interval with probability mass function P(X = k) = (l^k * e^(-l)) / k!, where l represents the average rate of events. Both are discrete distributions, with the Geometric focusing on the waiting time for a single event and the Poisson characterizing counts of events over continuous time or space.
Real-life Applications of Geometric Distribution
The geometric distribution models the number of trials until the first success, making it ideal for scenarios like quality control in manufacturing where the focus is on the first defective item found. It is also used in customer service to predict the number of calls before the first successful resolution. Unlike the Poisson distribution, which measures the count of events in a fixed interval, the geometric distribution emphasizes the waiting time for a single event, providing valuable insights in reliability testing and gambling probabilities.
Real-life Scenarios for Poisson Distribution
Poisson distribution models the number of events occurring in fixed intervals of time or space, making it ideal for real-life scenarios like counting the number of customer arrivals at a store, phone calls received by a call center, or accidents occurring at a traffic intersection. Unlike the geometric distribution, which focuses on the number of trials until the first success, Poisson distribution handles the frequency of events independently happening over a continuous domain. Key applications include predicting rare events, such as system failures or emergency room visits, where the mean event rate is known but exact timings vary randomly.
Parameter Interpretations and Meanings
The geometric distribution models the number of trials until the first success, parameterized by the probability p of success on each trial, where its mean is 1/p, representing the expected number of trials. The Poisson distribution counts the number of events occurring in a fixed interval, governed by the rate parameter l, with the mean equal to l, indicating the average event frequency per interval. While the geometric parameter p reflects success probability on discrete trials, the Poisson parameter l represents the continuous average rate of occurrences.
Assumptions Underlying Each Distribution
The Geometric distribution assumes a sequence of independent Bernoulli trials with a constant probability of success, modeling the number of trials until the first success occurs. The Poisson distribution assumes events occur independently over a fixed interval or region with a constant average rate, modeling the count of events in that interval. Both distributions rely on independence, but the Geometric focuses on discrete trials, whereas Poisson applies to events distributed in continuous time or space.
Comparing Probability Mass Functions
The geometric distribution's probability mass function (PMF) is defined as P(X = k) = (1 - p)^(k-1) * p for k = 1, 2, ..., representing the probability of the first success on the k-th trial, with parameter p indicating success probability per trial. In contrast, the Poisson distribution's PMF is given by P(X = k) = (l^k * e^(-l)) / k! for k = 0, 1, 2, ..., modeling the number of events occurring within a fixed interval with l as the average event rate. While the geometric PMF decreases exponentially with increasing k, emphasizing the waiting time for the first success, the Poisson PMF describes the distribution of count-based events that occur independently within a fixed time or space.
Advantages and Limitations of Each Distribution
The Geometric distribution excels in modeling the number of trials until the first success, offering simplicity and memoryless properties, but it assumes a constant success probability and may not fit data with varying event rates. The Poisson distribution effectively describes the number of events in fixed intervals, handling varying counts and rare events while assuming events occur independently and at a constant average rate, which can limit accuracy in clustered or overdispersed data. Selecting between Geometric and Poisson depends on data characteristics, such as the nature of event occurrences and memoryless behavior requirements.
Choosing the Right Distribution for Your Data
Choosing between the Geometric and Poisson distributions depends on the nature of your data and the event occurrence pattern. Use the Geometric distribution when modeling the number of trials until the first success in a sequence of independent Bernoulli trials with constant probability, reflecting discrete, "waiting time" data. Opt for the Poisson distribution when counting the number of events occurring within a fixed interval or region, especially for rare events with a known average rate and independent occurrences.
Geometric Infographic
 libterm.com
libterm.com