Artin groups, defined by specific generators and relations derived from Coxeter matrices, play a crucial role in geometric group theory and algebraic topology. They generalize braid groups and have applications in understanding complex algebraic structures and solving equations in groups. Explore the rest of this article to discover how Artin groups contribute to advancements in mathematical research and their practical implications.
Table of Comparison
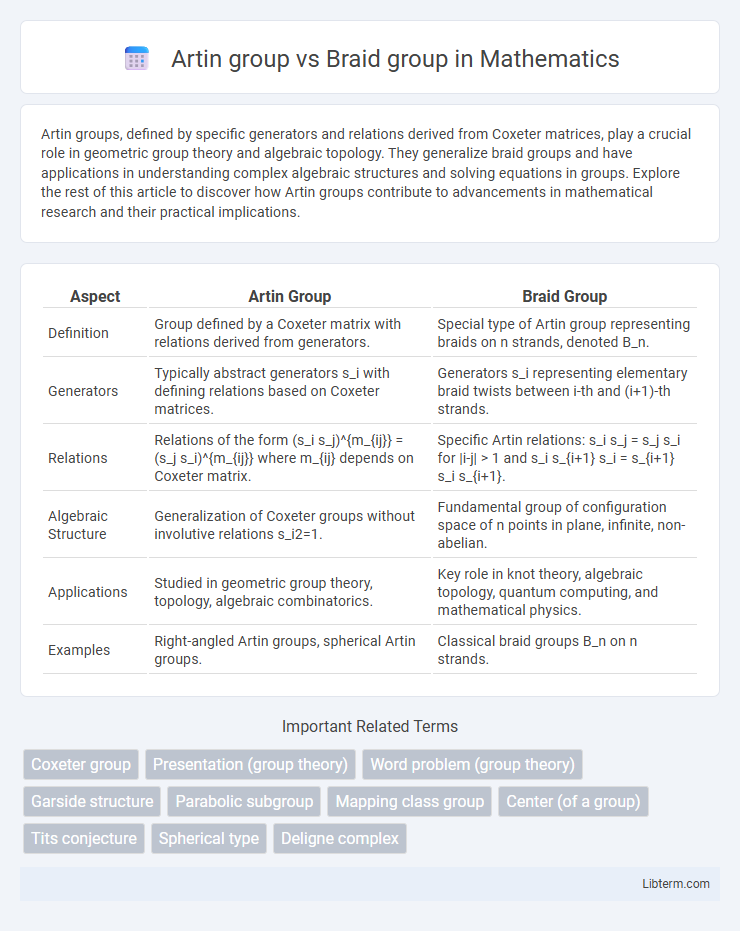
| Aspect | Artin Group | Braid Group |
|---|---|---|
| Definition | Group defined by a Coxeter matrix with relations derived from generators. | Special type of Artin group representing braids on n strands, denoted B_n. |
| Generators | Typically abstract generators s_i with defining relations based on Coxeter matrices. | Generators s_i representing elementary braid twists between i-th and (i+1)-th strands. |
| Relations | Relations of the form (s_i s_j)^{m_{ij}} = (s_j s_i)^{m_{ij}} where m_{ij} depends on Coxeter matrix. | Specific Artin relations: s_i s_j = s_j s_i for |i-j| > 1 and s_i s_{i+1} s_i = s_{i+1} s_i s_{i+1}. |
| Algebraic Structure | Generalization of Coxeter groups without involutive relations s_i2=1. | Fundamental group of configuration space of n points in plane, infinite, non-abelian. |
| Applications | Studied in geometric group theory, topology, algebraic combinatorics. | Key role in knot theory, algebraic topology, quantum computing, and mathematical physics. |
| Examples | Right-angled Artin groups, spherical Artin groups. | Classical braid groups B_n on n strands. |
Introduction to Artin Groups and Braid Groups
Artin groups are a class of groups defined by generators and relations derived from Coxeter groups, characterized by presentations with relations of the form \( (s_i s_j)^{m_{ij}} = (s_j s_i)^{m_{ij}} \) where \( m_{ij} \) encodes the interaction between generators. Braid groups, a fundamental example of Artin groups, correspond to the type \( A_{n-1} \) Coxeter system and are generated by elementary braids subject to the braid relations \( \sigma_i \sigma_{i+1} \sigma_i = \sigma_{i+1} \sigma_i \sigma_{i+1} \) and commutation relations \( \sigma_i \sigma_j = \sigma_j \sigma_i \) for \( |i-j| > 1 \). These groups play significant roles in various mathematical fields such as algebra, topology, and geometric group theory due to their rich algebraic structure and connection to configuration spaces.
Historical Background of Artin and Braid Groups
Introduced by Emil Artin in the 1920s, Artin groups generalize braid groups through presentations defined by generators and relations based on Coxeter graphs, reflecting symmetries in algebraic structures. Braid groups, initially studied by Artin himself, represent configurations of intertwined strands and have profound applications in topology, knot theory, and algebraic geometry. The historical development of these groups highlights Artin's foundational work connecting algebraic and geometric concepts, laying the groundwork for modern group theory and low-dimensional topology.
Defining Artin Groups: Key Concepts
Artin groups are defined by generators and relations derived from Coxeter matrices, generalizing braid groups which correspond to specific Coxeter types. Each Artin group presentation includes relations called braid relations, where two generators satisfy alternating product equalities that reflect the Coxeter graph's edges. Unlike braid groups defined by the standard Artin braid relations, Artin groups cover a broader class of groups by incorporating varying orders of generator interactions specified by the associated Coxeter system.
Defining Braid Groups: Core Principles
Braid groups are defined based on generators corresponding to the elementary braids and relations that capture the allowed crossing interactions between strands, formalized through Artin's presentation. Each generator represents the crossing of two adjacent strands, and the defining relations ensure consistency with the Reidemeister moves for braids, including the fundamental braid relations s_i s_{i+1} s_i = s_{i+1} s_i s_{i+1} and commutation relations s_i s_j = s_j s_i for |i - j| > 1. These core principles establish braid groups as specific examples of Artin groups, distinguished by their geometric interpretation and algebraic structure.
Relationship Between Artin Groups and Braid Groups
Artin groups generalize braid groups by extending their defining relations, where braid groups are special cases of Artin groups associated with finite Coxeter systems. The fundamental relationship is that every braid group serves as an Artin group of type A, with Artin groups encompassing a broader family defined by diverse Coxeter matrices. This connection highlights the role of Artin groups in studying geometric group theory and algebraic structures derived from braid groups.
Structural Differences: Generators and Relations
Artin groups are defined by a set of generators subject to relations determined by a Coxeter matrix, where each pair of generators satisfies a specific braid-like relation of varying length depending on the matrix entries. Braid groups, a particular case of Artin groups, have generators representing elementary braids with relations reflecting the classical braid relations, typically involving only commuting and the third Reidemeister move relations. The structural difference lies in the generality of Artin groups permitting diverse and complex relations based on arbitrary Coxeter diagrams, while braid groups impose a standardized set corresponding to type A Coxeter systems.
Geometric and Topological Interpretations
Artin groups generalize braid groups by associating with Coxeter graphs, providing a rich structure for geometric group theory. Braid groups correspond to configurations of points in the plane, interpreted as isotopy classes of braids, closely linked to the fundamental group of the configuration space. Geometrically, Artin groups act on CAT(0) spaces or hyperplane arrangements, while braid groups naturally represent motion groups with topological applications in knot theory and mapping class groups.
Applications in Mathematics and Science
Artin groups and braid groups play crucial roles in topology, algebra, and mathematical physics, with braid groups being prominent in knot theory, quantum computing, and the study of statistical mechanics via their connection to the Yang-Baxter equation. Artin groups generalize braid groups and find applications in geometric group theory, singularity theory, and the classification of algebraic varieties through their actions on complex hyperplane arrangements. Both groups contribute to advancements in cryptography algorithms and understanding fundamental groups of configuration spaces in robotics and molecular biology.
Common Problems and Research Directions
Artin groups and braid groups both present complex challenges in understanding their algebraic and geometric properties, such as the word and conjugacy problems, which remain central yet unresolved for many classes. Research often focuses on developing novel algorithms and geometric interpretations to classify these groups' actions on associated spaces, enhancing insight into their automorphism groups and subgroup structures. Advances in low-dimensional topology and geometric group theory drive exploration into their boundaries, growth functions, and representation theory, aiming to link these groups with broader mathematical frameworks like hyperbolic geometry and cluster algebras.
Summary: Artin Group vs Braid Group
Artin groups generalize braid groups through presentations defined by specific Coxeter matrices, where braid groups arise as particular Artin groups associated with type A Coxeter systems. Braid groups exhibit rich algebraic structures and topological significance, notably representing motions of points in a plane, while Artin groups extend these concepts to broader Coxeter-based relations. The distinction lies in the underlying generators and relations, with braid groups providing a foundational example within the larger family of Artin groups.
Artin group Infographic
 libterm.com
libterm.com