Cech cohomology provides a powerful tool for studying the global properties of topological spaces by analyzing their open coverings and associated cochain complexes. It captures information about the space's structure that is often invisible to more elementary invariants, playing a crucial role in algebraic topology and sheaf theory. Explore the rest of this article to uncover how Cech cohomology can deepen your understanding of complex topological phenomena.
Table of Comparison
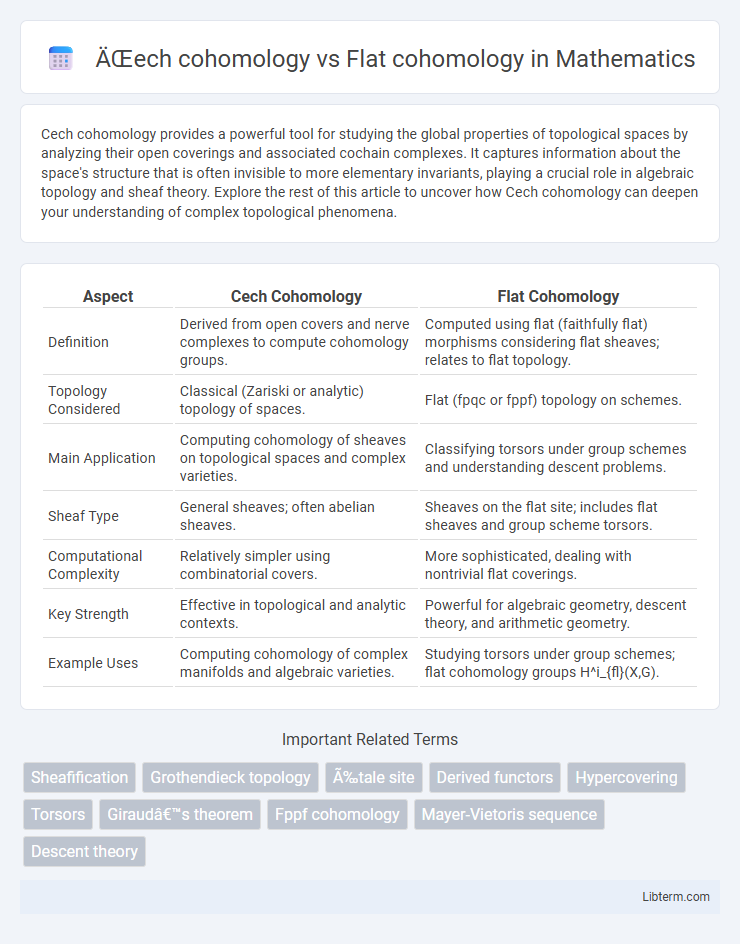
| Aspect | Cech Cohomology | Flat Cohomology |
|---|---|---|
| Definition | Derived from open covers and nerve complexes to compute cohomology groups. | Computed using flat (faithfully flat) morphisms considering flat sheaves; relates to flat topology. |
| Topology Considered | Classical (Zariski or analytic) topology of spaces. | Flat (fpqc or fppf) topology on schemes. |
| Main Application | Computing cohomology of sheaves on topological spaces and complex varieties. | Classifying torsors under group schemes and understanding descent problems. |
| Sheaf Type | General sheaves; often abelian sheaves. | Sheaves on the flat site; includes flat sheaves and group scheme torsors. |
| Computational Complexity | Relatively simpler using combinatorial covers. | More sophisticated, dealing with nontrivial flat coverings. |
| Key Strength | Effective in topological and analytic contexts. | Powerful for algebraic geometry, descent theory, and arithmetic geometry. |
| Example Uses | Computing cohomology of complex manifolds and algebraic varieties. | Studying torsors under group schemes; flat cohomology groups H^i_{fl}(X,G). |
Introduction to Čech Cohomology
Cech cohomology provides a computational tool to study the topological structure of spaces using open covers and simplicial methods, making it fundamental in algebraic topology. It captures global properties by analyzing locally defined data, enabling classification of fiber bundles and sheaf cohomology computations. Compared to Flat cohomology, Cech cohomology emphasizes combinatorial methods and continuous mappings, often serving as an accessible introduction to more advanced cohomology theories.
Fundamentals of Flat Cohomology
Flat cohomology is a topological invariant defined using the flat topology on schemes, focusing on faithfully flat morphisms to refine the classical etale and Zariski cohomologies. Unlike Cech cohomology, which computes cohomology via open covers and nerve constructions, flat cohomology leverages the fppf site to capture subtle torsion phenomena and more general sheaf cohomology classes. Its fundamental importance lies in classifying torsors under group schemes, particularly for non-etale and non-reduced structures, making it essential in arithmetic geometry and deformation theory.
Comparing Topological and Grothendieck Sites
Cech cohomology is traditionally defined using open covers in the classical topological setting, capturing cohomological information via simplicial methods on topological spaces. Flat cohomology, developed in the framework of Grothendieck sites, uses faithfully flat morphisms and sheaves of modules to detect finer algebraic structures invisible to ordinary topological covers. Comparing these approaches reveals that while Cech cohomology aligns with the etale or Zariski topology, flat cohomology operates on the flat site, enabling cohomological analysis of torsors and crystalline phenomena beyond topological constraints.
The Role of Coverings in Each Theory
Cech cohomology relies on open coverings of a topological space to construct cochain complexes, capturing global topological information through intersections of these covers. Flat cohomology uses flat (faithfully flat) morphisms of schemes as coverings in the fppf topology, enabling the study of more general sheaves and torsors beyond the etale setting. The choice of coverings reflects the distinct geometric contexts: Cech cohomology uses topological coverings suited for classical spaces, whereas flat cohomology employs algebraic coverings tailored for algebraic geometry and arithmetic applications.
Sheaf Conditions: Čech vs Flat Context
Cech cohomology relies on the classical sheaf condition with respect to open covers of a topological space, ensuring that sections agree on overlaps to provide a computationally accessible approach for locally defined data. Flat cohomology, in contrast, operates in the context of the flat (faithfully flat and quasi-compact) topology on schemes, where the sheaf condition is imposed for coverings formed by flat morphisms, capturing more subtle algebraic and geometric properties than the ordinary topology. The difference in sheaf conditions reflects the broader applicability of flat cohomology in algebraic geometry, especially for detecting torsors and obstructions that Cech cohomology might miss in nontrivial flat covers.
Functoriality and Exact Sequences
Cech cohomology and Flat cohomology both provide tools to analyze sheaf cohomology, but they differ in their functorial behavior and treatment of exact sequences. Cech cohomology, constructed via open coverings, often lacks full functoriality and may fail to preserve exactness in certain sequences, especially for non-paracompact spaces. Flat cohomology, defined through flat site and faithfully flat descent, exhibits stronger functorial properties and better exact sequence compatibility, making it more suitable for studying torsors and cohomological invariants in algebraic geometry.
Examples: Computing Čech and Flat Cohomology
Computing Cech cohomology involves covering a topological space with open sets and analyzing the intersections to capture global topological information, often applied in algebraic topology and complex geometry. Flat cohomology, used primarily in algebraic geometry, encodes finer structures by employing the flat (fppf) topology, allowing for the study of torsors and descent theory over schemes, with calculations often involving sheaves of flat modules. Concrete examples include computing Cech cohomology of a sheaf on a simplicial complex and calculating flat cohomology groups to classify vector bundles or torsors under group schemes, highlighting differences in topological versus algebraic contexts.
Strengths and Limitations of Čech Cohomology
Cech cohomology provides an intuitive and computationally accessible framework for sheaf cohomology on sufficiently nice topological spaces and is particularly powerful for paracompact Hausdorff spaces where it coincides with sheaf cohomology. Its strengths lie in explicit coverings and combinatorial methods that facilitate calculations in algebraic topology and complex geometry. However, Cech cohomology faces limitations with non-paracompact spaces, lacks robustness in handling general sheaves over arbitrary sites, and can fail to capture finer cohomological invariants that flat cohomology addresses through a more flexible and general homological algebraic approach.
When to Choose Flat Cohomology
Flat cohomology is preferred over Cech cohomology when dealing with non-abelian sheaves or sheaves of noncommutative groups, as it better handles torsion phenomena and nontrivial extensions in algebraic geometry. It is particularly effective in the context of schemes with flat covers, allowing for a more flexible and general cohomological theory that captures finer geometric and arithmetic information. When working on flat sites or considering descent problems in the flat topology, flat cohomology provides essential tools that Cech cohomology cannot adequately address.
Applications and Further Perspectives
Cech cohomology is extensively applied in algebraic topology, providing critical tools for classifying sheaves and analyzing topological spaces through open covers, which aids in computations of sheaf cohomology in complex geometry and algebraic varieties. Flat cohomology, closely related to fppf cohomology, is essential in arithmetic geometry for studying torsors under flat group schemes, especially in the context of descent theory, deformation theory, and the classification of principal bundles over schemes. Future perspectives emphasize the integration of Cech and flat cohomology methods in non-abelian cohomology and derived algebraic geometry, deepening the understanding of geometric structures and enhancing applications in moduli problems and arithmetic dualities.
Čech cohomology Infographic
 libterm.com
libterm.com