The supremum of a set is the smallest value that is greater than or equal to every element within that set, serving as a crucial concept in mathematical analysis. It is particularly important in fields like real analysis and optimization, where understanding bounds helps in solving complex problems. Explore the rest of the article to deepen your understanding of how supremum functions across different mathematical contexts.
Table of Comparison
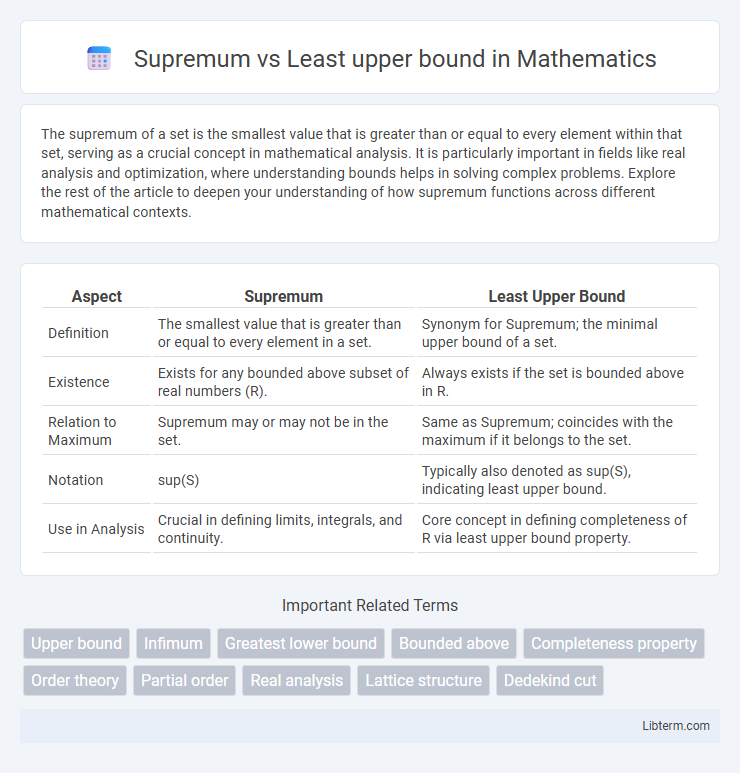
| Aspect | Supremum | Least Upper Bound |
|---|---|---|
| Definition | The smallest value that is greater than or equal to every element in a set. | Synonym for Supremum; the minimal upper bound of a set. |
| Existence | Exists for any bounded above subset of real numbers (R). | Always exists if the set is bounded above in R. |
| Relation to Maximum | Supremum may or may not be in the set. | Same as Supremum; coincides with the maximum if it belongs to the set. |
| Notation | sup(S) | Typically also denoted as sup(S), indicating least upper bound. |
| Use in Analysis | Crucial in defining limits, integrals, and continuity. | Core concept in defining completeness of R via least upper bound property. |
Introduction to Supremum and Least Upper Bound
The supremum, or least upper bound, is the smallest value that is greater than or equal to every element in a set, particularly in ordered sets such as the real numbers. It may or may not be an element of the set but serves as a critical concept in real analysis for bounding sets from above. Understanding the supremum is essential in fields like calculus and optimization where limits and bounds define the behavior and convergence of sequences and functions.
Definition of Supremum
The supremum, or least upper bound, of a set is the smallest value that is greater than or equal to every element in the set, even if that value is not contained within the set itself. In mathematical terms, for a set S, the supremum sup(S) satisfies two conditions: it is an upper bound of S, and any smaller number is not an upper bound. This concept is fundamental in real analysis, particularly in the study of ordered sets and completeness of the real numbers.
Understanding the Least Upper Bound
The least upper bound, or supremum, of a set is the smallest value that is greater than or equal to every element in the set, ensuring it serves as a boundary without being exceeded by any member. Unlike a general upper bound, the least upper bound is unique and may or may not belong to the set itself, playing a crucial role in real analysis and order theory. Understanding the least upper bound illuminates concepts such as completeness of the real numbers and the convergence of sequences.
Supremum vs Least Upper Bound: Semantic Differences
Supremum and Least Upper Bound are terms often used interchangeably in mathematics, especially in order theory and real analysis, but they carry subtle semantic distinctions. The supremum refers to the smallest element that is greater than or equal to every element in a set, encompassing cases where the supremum may not belong to the set, while the Least Upper Bound is strictly defined as the minimal upper bound without implying set membership. Understanding this nuance is crucial in contexts like non-complete ordered sets, where a supremum might exist outside the set, highlighting the semantic precision required in rigorous mathematical proofs.
Mathematical Properties of Supremum
The supremum of a set is the smallest number that is greater than or equal to every element in the set, ensuring it serves as a least upper bound if it exists within the extended real numbers. It possesses key mathematical properties such as uniqueness, the property that no element in the set exceeds the supremum, and it may or may not belong to the set itself. The concept of supremum generalizes the maximum value, particularly in sets that do not contain a maximum, making it fundamental in real analysis and order theory.
Role of Least Upper Bound in Analysis
The least upper bound, or supremum, plays a crucial role in real analysis by ensuring the completeness of the real numbers, where every non-empty set bounded above has a supremum within the reals. This property underpins key theorems such as the Monotone Convergence Theorem and facilitates the rigorous definition of limits and integrals. Establishing the existence of least upper bounds enables precise control over infinite processes and aids in characterizing continuity and compactness in metric spaces.
Examples Illustrating Supremum and Least Upper Bound
The supremum and least upper bound of a set often coincide, such as in the set \(A = \{x \in \mathbb{R} : x < 3\}\), where 3 is the supremum and the least upper bound but not an element of the set. For the set \(B = \{1, 2, 3\}\), the supremum and least upper bound are both 3, which is also contained within the set. Sets without a maximum element, like open intervals, demonstrate that the supremum is the smallest number greater than or equal to all elements, fulfilling the role of least upper bound.
Importance in Real Analysis and Set Theory
The supremum, or least upper bound, is a fundamental concept in real analysis and set theory that ensures every bounded set of real numbers has a minimal upper bound within the real number system, crucial for defining completeness. This property underpins the construction of the real numbers, enabling rigorous definitions of limits, convergence, and continuity. In set theory, the supremum aids in ordering structures and supports the development of lattice theory and measure theory by providing a coherent framework for upper bounds.
Common Misconceptions and Clarifications
The supremum and least upper bound often cause confusion because they are mathematically equivalent concepts, yet the supremum may not belong to the set while the least upper bound must be the smallest number that is greater than or equal to every element in the set. A common misconception is treating the supremum as always an element within the set, which is not true for sets that are open or do not contain their bounds. Clarifying this distinction is crucial in real analysis and helps avoid errors in understanding limit processes and boundedness.
Conclusion: Choosing the Right Terminology
Supremum and least upper bound both describe the smallest value that is greater than or equal to every element in a set, but supremum is preferred in advanced mathematical analysis, especially within real analysis and order theory contexts. Least upper bound is often used in more intuitive or introductory settings, emphasizing its role as the minimal boundary that a set does not exceed. Selecting the appropriate term depends on the audience and mathematical rigor required, ensuring clarity and precision in communication.
Supremum Infographic
 libterm.com
libterm.com