A Markushevich basis is a special type of basis in functional analysis characterized by biorthogonality and totality conditions for Banach spaces. It plays a crucial role in representing elements and understanding the geometry of infinite-dimensional vector spaces. Explore the full article to deepen your understanding of the Markushevich basis and its applications in modern analysis.
Table of Comparison
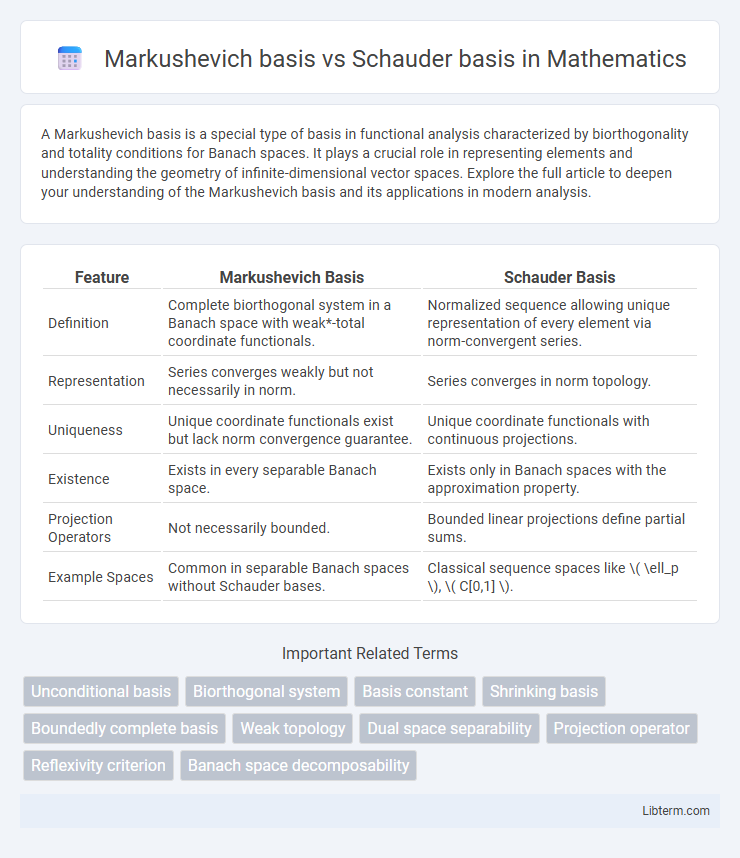
| Feature | Markushevich Basis | Schauder Basis |
|---|---|---|
| Definition | Complete biorthogonal system in a Banach space with weak*-total coordinate functionals. | Normalized sequence allowing unique representation of every element via norm-convergent series. |
| Representation | Series converges weakly but not necessarily in norm. | Series converges in norm topology. |
| Uniqueness | Unique coordinate functionals exist but lack norm convergence guarantee. | Unique coordinate functionals with continuous projections. |
| Existence | Exists in every separable Banach space. | Exists only in Banach spaces with the approximation property. |
| Projection Operators | Not necessarily bounded. | Bounded linear projections define partial sums. |
| Example Spaces | Common in separable Banach spaces without Schauder bases. | Classical sequence spaces like \( \ell_p \), \( C[0,1] \). |
Introduction to Functional Bases in Banach Spaces
Markushevich bases and Schauder bases are fundamental concepts in the study of functional bases in Banach spaces, each providing a framework for representing elements. A Schauder basis allows every element in a Banach space to be uniquely represented as a norm-convergent series, ensuring strong topological and linear structure control. Markushevich bases, also known as biorthogonal systems, generalize this by requiring only weak* biorthogonality without norm convergence, making them crucial for analyzing dual spaces and reflexivity in functional analysis.
Defining Markushevich Basis: Key Concepts
A Markushevich basis in a Banach space is a biorthogonal system \((x_n, f_n)\) where \((x_n)\) is a sequence in the space and \((f_n)\) is a sequence in the dual, satisfying \(f_n(x_m) = \delta_{nm}\), dense span of \((x_n)\), and weak*-dense span of \((f_n)\) in the dual. Unlike a Schauder basis, which requires norm convergence of series expansions, a Markushevich basis only guarantees weak convergence and biorthogonality, providing a more flexible framework for decompositions in non-separable or non-reflexive spaces. This basis is crucial in functional analysis for studying the dual space structure and for representation of elements when norm convergence is too strong a condition.
Schauder Basis Explained: Properties and Examples
A Schauder basis in a Banach space is a sequence of vectors such that every element in the space can be uniquely represented as a convergent series of these vectors, enabling coefficient extraction via continuous linear functionals. Its fundamental properties include norm convergence of partial sums to the vector and biorthogonality in the associated dual system, which facilitates practical expansions in functional analysis. Examples of Schauder bases include the classical Haar basis in Lp spaces and the sequence of unit vectors in lp spaces, demonstrating their pivotal role in approximating functions and solving operator equations.
Historical Background and Development
Markushevich bases, introduced by A.I. Markushevich in the 1920s, emerged from efforts to generalize Schauder bases in Banach spaces by allowing biorthogonal sequences that are not necessarily norm-convergent. Schauder bases, dating back to Juliusz Schauder's work in the late 1930s, provided a foundation for representing elements in separable Banach spaces via norm-convergent series expansions. The historical development of these bases reflects the evolution from classical notions of series representation in functional analysis to more flexible decompositions accommodating broader classes of topological vector spaces.
Existence Theorems: Markushevich vs. Schauder Basis
The existence theorem for a Schauder basis ensures that every separable Banach space admits a countable sequence allowing unique norm-convergent expansions of any element, highlighting its strong structural property. Markushevich bases, also known as M-bases, guarantee the existence of biorthogonal systems in separable Banach spaces, ensuring weak* density but not necessarily norm convergence. The key distinction lies in the completeness criterion: Schauder bases provide norm convergence and reconstruction, while Markushevich bases ensure biorthogonality and totality without requiring norm convergence of expansions.
Separability and Applications in Infinite Dimensions
A Markushevich basis, also known as a biorthogonal system, provides a weaker form of basis in separable Banach spaces compared to a Schauder basis, as it does not require norm convergence of expansions but ensures totality and biorthogonality. Schauder bases guarantee norm-convergent expansions for every element in separable infinite-dimensional spaces, supporting more robust functional analysis and approximation techniques. Markushevich bases find applications in the study of duality and reflexivity properties of infinite-dimensional spaces, while Schauder bases are fundamental in constructive methods and numerical analysis.
Comparison of Uniqueness and Reconstruction
A Schauder basis guarantees unique representation of every element in a Banach space as a convergent series of basis vectors, ensuring stable reconstruction via continuous coordinate functionals. Markushevich bases, also known as total minimal systems, allow biorthogonal functionals but do not ensure unique or stable expansions, leading to potential non-uniqueness in reconstruction. The key distinction lies in that every Schauder basis is a Markushevich basis with unique expansions, whereas Markushevich bases may lack uniqueness and convergence properties critical for reliable reconstruction.
Dual Space Relationships: Biorthogonal Systems
A Markushevich basis, also known as an M-basis, consists of a biorthogonal system \((x_n, f_n)\) in a Banach space \(X\) and its dual \(X^*\), where each \(x_n \in X\) and \(f_n \in X^*\) satisfy \(f_n(x_m) = \delta_{nm}\) and the span of \(\{x_n\}\) is dense in \(X\), while \(\{f_n\}\) is norming for \(X\). In contrast, a Schauder basis ensures unique coefficient expansions with continuous coordinate projections, which strongly link the basis in \(X\) to corresponding coordinate functionals in \(X^*\), establishing a more rigid dual space correspondence. The primary distinction in dual space relationships lies in the weaker continuity properties of functionals in Markushevich bases, which yields biorthogonality without necessarily providing bounded projections, unlike the Schauder basis framework that induces a dual sequence forming a basis for a complemented subspace of \(X^*\).
Applications in Analysis and Operator Theory
Markushevich bases, also known as M-bases, provide a biorthogonal system useful for representing elements in separable Banach spaces, enabling the study of weak* topologies in dual spaces. Schauder bases, characterized by norm-convergent expansions, are instrumental in approximating operators and analyzing compactness properties in operator theory. Applications in analysis include spectral theory and the structural study of Banach spaces, where Schauder bases facilitate explicit norm computations, while Markushevich bases support duality arguments and the extension of linear functionals.
Summary of Differences and Research Directions
Markushevich bases, also known as M-bases, differ from Schauder bases primarily in their biorthogonality and conditional completeness, whereas Schauder bases guarantee norm convergence of expansions in Banach spaces. Research directions emphasize exploring the stability of M-bases under perturbations, their applications in non-separable spaces, and the development of constructive methods for approximations in function spaces. Advances aim to deepen understanding of basis representations in complex topological vector spaces and optimize computational algorithms in functional analysis.
Markushevich basis Infographic
 libterm.com
libterm.com