The spectral gap refers to the difference between the largest and second-largest eigenvalues of a matrix or operator, playing a crucial role in determining the stability and convergence rate of various systems. It is a key concept in fields like quantum mechanics, Markov chains, and graph theory, where a larger spectral gap often implies faster mixing or better robustness. Explore the rest of this article to understand how the spectral gap impacts your applications and why it matters.
Table of Comparison
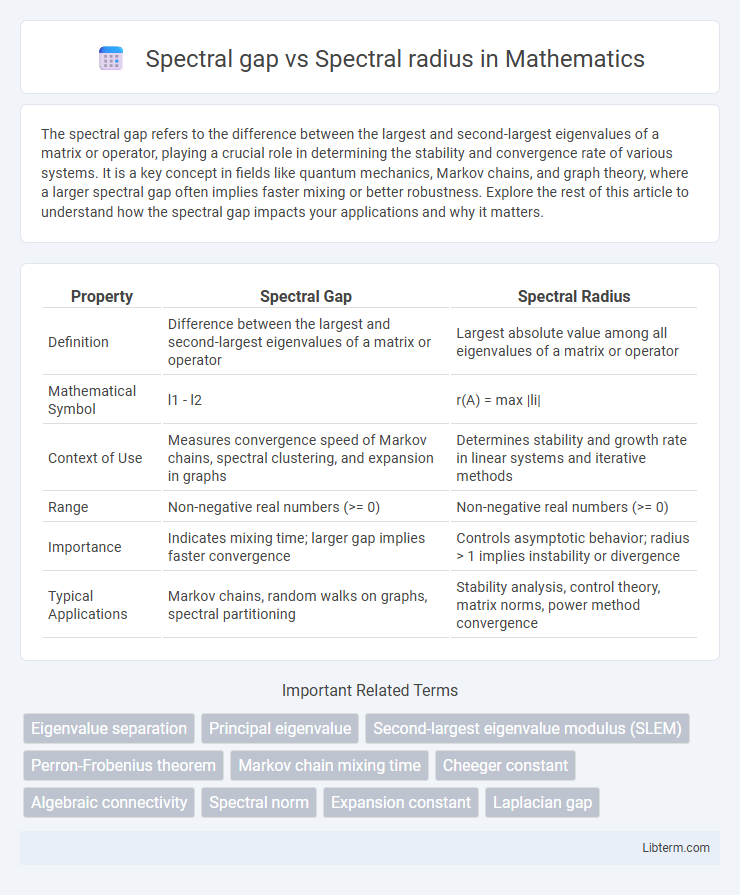
| Property | Spectral Gap | Spectral Radius |
|---|---|---|
| Definition | Difference between the largest and second-largest eigenvalues of a matrix or operator | Largest absolute value among all eigenvalues of a matrix or operator |
| Mathematical Symbol | l1 - l2 | r(A) = max |li| |
| Context of Use | Measures convergence speed of Markov chains, spectral clustering, and expansion in graphs | Determines stability and growth rate in linear systems and iterative methods |
| Range | Non-negative real numbers (>= 0) | Non-negative real numbers (>= 0) |
| Importance | Indicates mixing time; larger gap implies faster convergence | Controls asymptotic behavior; radius > 1 implies instability or divergence |
| Typical Applications | Markov chains, random walks on graphs, spectral partitioning | Stability analysis, control theory, matrix norms, power method convergence |
Introduction to Spectral Properties in Linear Algebra
Spectral gap refers to the difference between the largest and second-largest eigenvalues of a matrix, playing a crucial role in convergence rates of iterative methods and stability analysis. Spectral radius denotes the largest absolute value among all eigenvalues and primarily determines the long-term behavior of matrix powers in dynamical systems. Understanding spectral gap and spectral radius is fundamental in linear algebra for analyzing matrix behavior, eigenvalue distributions, and applications in numerical algorithms.
Defining Spectral Gap: Concept and Importance
The spectral gap refers to the difference between the largest and second-largest eigenvalues of a matrix or operator, reflecting the system's convergence rate to equilibrium. A larger spectral gap indicates faster mixing times and improved stability in Markov chains, graph Laplacians, and quantum mechanics. Understanding the spectral gap is crucial for analyzing the robustness of networks, optimizing algorithms, and assessing the performance of stochastic processes.
Understanding the Spectral Radius of a Matrix
The spectral radius of a matrix is defined as the largest absolute value among its eigenvalues, serving as a crucial measure in stability analysis and iterative methods. It provides insight into the long-term behavior of matrix powers and is instrumental in determining convergence rates for algorithms such as power iteration and Markov chains. Understanding the spectral radius helps predict system dynamics and optimize performance in numerical linear algebra applications.
Mathematical Relationship: Spectral Gap vs Spectral Radius
The spectral gap is defined as the difference between the spectral radius and the magnitude of the second-largest eigenvalue of a matrix, providing a measure of how quickly powers of the matrix converge. Spectral radius represents the largest absolute value among all eigenvalues, indicating the dominant growth rate of the associated linear transformation. A larger spectral gap implies faster convergence rates in iterative processes, highlighting its critical role in stability and mixing time analyses.
Spectral Gap and Its Role in Convergence Analysis
The spectral gap is defined as the difference between the largest and second-largest eigenvalues of a matrix or operator, playing a crucial role in convergence analysis by determining the rate at which iterative methods or Markov chains approach equilibrium. A larger spectral gap implies faster convergence and greater stability in processes such as random walks, consensus algorithms, and numerical solvers. Understanding the spectral gap enables optimization of algorithm performance by controlling mixing times and error decay rates.
Applications of Spectral Radius in Stability and Control
Spectral radius, defined as the largest absolute eigenvalue of a matrix, plays a crucial role in assessing system stability and control in fields such as control theory and dynamical systems. Its value determines the asymptotic behavior of linear systems, where a spectral radius less than one ensures stability in discrete-time systems and influences the design of stable feedback controllers. In contrast, the spectral gap, representing the difference between the largest and second-largest eigenvalues, often relates to convergence rates but is less directly linked to stability than the spectral radius.
Comparing Implications in Graph Theory and Markov Chains
Spectral gap measures the difference between the largest and second-largest eigenvalues of a graph's adjacency or transition matrix, directly influencing convergence rates and mixing times in Markov chains. A larger spectral gap indicates rapid convergence to a stationary distribution and enhanced graph expansion properties, whereas spectral radius, the largest absolute eigenvalue, governs the overall growth or decay dynamics in iterative processes on graphs. Comparing these, spectral gap provides insights into stability and efficiency of random walks, while spectral radius offers bounds on long-term behavior and spectral norms relevant in network connectivity and diffusion phenomena.
Calculation Methods: Spectral Gap versus Spectral Radius
Spectral radius is calculated as the largest absolute value of the eigenvalues of a matrix, representing its dominant eigenvalue magnitude, while the spectral gap is defined as the difference between the largest and second-largest eigenvalues in absolute value, indicating how quickly a process converges to equilibrium. The power iteration method is commonly used to estimate the spectral radius, focusing on the dominant eigenvector, whereas the spectral gap calculation requires identifying both the first and second-largest eigenvalues typically via QR algorithm or Lanczos iteration for sparse matrices. Accurate spectral gap estimation is critical in applications such as Markov chains and graph theory for assessing mixing times and connectivity, while spectral radius provides key stability criteria in dynamical systems and control theory.
Practical Examples and Case Studies
The spectral gap, defined as the difference between the largest and second-largest eigenvalues of a matrix, plays a critical role in assessing convergence rates in Markov chains and the mixing times in networks, as seen in Google's PageRank algorithm where a larger spectral gap ensures faster information propagation. In contrast, the spectral radius, representing the largest absolute eigenvalue, is crucial in stability analysis of dynamical systems and iterative methods, such as in power grid stability where controlling the spectral radius prevents voltage oscillations. Case studies in epidemiology employ spectral gap to evaluate the spread rate of diseases through contact networks, while control theory extensively uses spectral radius to ensure system robustness under perturbations.
Summary: Choosing Between Spectral Gap and Spectral Radius
Spectral gap measures the difference between the largest and second-largest eigenvalues, providing insights into convergence speed and stability in graphs and Markov chains. Spectral radius, the largest absolute eigenvalue, indicates the dominant growth rate or system behavior over time. Selecting between spectral gap and spectral radius depends on the analysis goal: spectral gap suits mixing time and expansion properties, while spectral radius is optimal for stability and asymptotic behavior evaluations.
Spectral gap Infographic
 libterm.com
libterm.com