The cup product is a fundamental operation in algebraic topology that combines cohomology classes to form new classes, enriching the algebraic structure of topological spaces. It allows for the construction of a graded ring called the cohomology ring, which encodes important geometric and topological information. Explore the rest of this article to understand how the cup product enhances your study of space and structure.
Table of Comparison
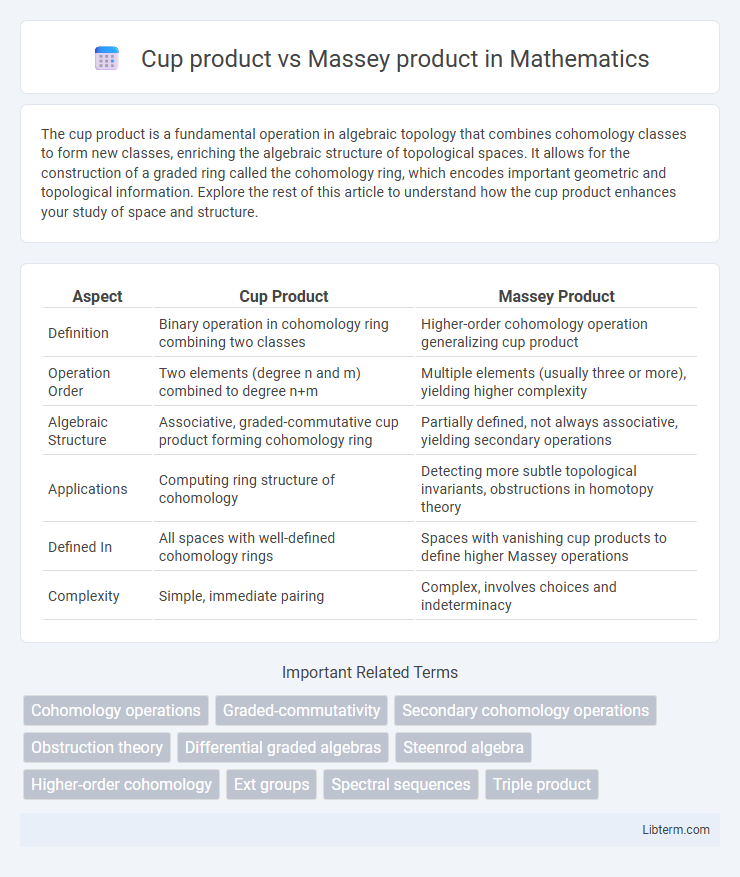
| Aspect | Cup Product | Massey Product |
|---|---|---|
| Definition | Binary operation in cohomology ring combining two classes | Higher-order cohomology operation generalizing cup product |
| Operation Order | Two elements (degree n and m) combined to degree n+m | Multiple elements (usually three or more), yielding higher complexity |
| Algebraic Structure | Associative, graded-commutative cup product forming cohomology ring | Partially defined, not always associative, yielding secondary operations |
| Applications | Computing ring structure of cohomology | Detecting more subtle topological invariants, obstructions in homotopy theory |
| Defined In | All spaces with well-defined cohomology rings | Spaces with vanishing cup products to define higher Massey operations |
| Complexity | Simple, immediate pairing | Complex, involves choices and indeterminacy |
Introduction to Cohomology Operations
Cup product is a fundamental cohomology operation that combines two cohomology classes to produce another class in the cohomology ring, capturing the algebraic structure of topological spaces. Massey product generalizes the cup product by detecting higher-order linking phenomena not visible through standard cup products, providing more refined invariants in the study of topological and algebraic structures. Both operations play essential roles in algebraic topology for understanding the interactions between cohomology classes and the underlying geometry of spaces.
The Foundations of the Cup Product
The foundational concept of the cup product in cohomology originates from the algebraic structure on cochain complexes, establishing a graded-commutative ring that encodes the intersection properties of topological spaces. This bilinear operation provides a product on cohomology groups \(H^*(X; R)\), enabling the calculation of invariants that detect finer topological features than linear invariants alone. Compared to the higher-order Massey product, the cup product is a primary operation, fundamental for building more complex structures in homotopy theory and spectral sequences.
Defining the Massey Product
The Massey product generalizes the cup product by capturing higher-order cohomology operations in differential graded algebras or cochain complexes. It is defined when certain lower cup products vanish, using a sequence of cohomology classes and their null-homotopies to produce multi-valued cohomology classes in higher degrees. Unlike the binary cup product, the Massey product reveals intricate algebraic structures and obstructions in topology that detect non-trivial linking phenomena.
Algebraic Structures in Cohomology
Cup products define a bilinear, associative, and graded-commutative multiplication in cohomology, establishing a ring structure known as the cohomology ring. Massey products extend the cup product by capturing higher-order cohomological operations that detect nontrivial linking phenomena not detected by cup products alone. These higher-order operations provide richer algebraic invariants in differential graded algebras and topological spaces, revealing intricate relations in the underlying algebraic structures of cohomology.
Computation: Cup Product vs Massey Product
The cup product in cohomology is computed using the straightforward pairing of cochains, providing a bilinear and associative operation that yields elements in the cohomology ring. In contrast, Massey products require solving higher-order cohomology extension problems, involving choices of cochain representatives and homotopies, making their computation significantly more complex and often only partially defined. Computationally, cup products are algorithmically simpler and systematically computable, whereas Massey products capture intricate secondary algebraic structures that reveal deeper topological information beyond what cup products detect.
Geometric Interpretation of Both Products
The Cup product in cohomology represents the intersection of cohomology classes corresponding to geometric subspaces, encoding how these subspaces overlap or intersect within a topological space. Massey products extend this idea by capturing higher-order intersections and linking phenomena that cannot be detected by simple pairwise cup products, revealing intricate configurations of cycles that manifest in the space's topology. Geometrically, while cup products reflect direct, two-fold intersections, Massey products describe complex, multi-layered interactions among classes, often associated with linking and obstruction phenomena in the underlying manifold.
Examples Demonstrating Cup and Massey Products
Cup products in cohomology provide a bilinear operation combining classes, illustrated in the cohomology ring of the torus \(T^2\) where \(H^1(T^2) \otimes H^1(T^2) \to H^2(T^2)\) forms a nontrivial product representing the fundamental class. Massey products generalize cup products to higher-order operations, exemplified by the Borromean rings link complement where triple Massey products detect linking information invisible to cup products. These examples demonstrate that while cup products capture basic intersection information, Massey products reveal deeper, secondary cohomological structures essential in algebraic topology and homotopy theory.
Obstructions and Higher Cohomology Operations
The Cup product serves as a primary bilinear operation in cohomology, essential for detecting basic algebraic structures but limited in revealing subtle obstructions in higher cohomology groups. Massey products generalize the Cup product to multiple cohomology classes, providing higher cohomology operations that capture intricate linking phenomena and detect obstructions unresolved by standard cup products. These higher operations are pivotal in homotopy theory and deformation problems, encoding secondary structure and detecting nontrivial extensions in chain complexes.
Applications in Topology and Algebra
Cup products are fundamental in cohomology rings, providing algebraic structures that classify topological spaces with applications in characteristic classes and fiber bundles. Massey products extend cup products by detecting higher-order linking information in cohomology, offering powerful tools for distinguishing complex spaces and studying formality in differential graded algebras. Both products play critical roles in analyzing the topology of manifolds, configuration spaces, and in obstruction theory for algebraic structures.
Key Differences and Significance
The Cup product is a bilinear operation in cohomology that combines two cohomology classes to produce a new class, serving as a foundational tool in algebraic topology for defining ring structures on cohomology groups. In contrast, the Massey product is a higher-order cohomology operation that generalizes the Cup product by capturing more subtle algebraic structures and detecting nontrivial linking phenomena not visible through Cup products alone. The significance of Massey products lies in their ability to reveal deeper topological invariants and obstructions in spaces, particularly in the study of differential graded algebras and the formality of manifolds.
Cup product Infographic
 libterm.com
libterm.com