Perverse sheaves are a powerful tool in algebraic geometry and topology, providing deep insights into the study of singular spaces and their cohomological properties. They generalize the notion of local systems and allow for the precise analysis of the topology of complex algebraic varieties. Explore the rest of this article to understand how perverse sheaves can enhance your knowledge of geometric and topological structures.
Table of Comparison
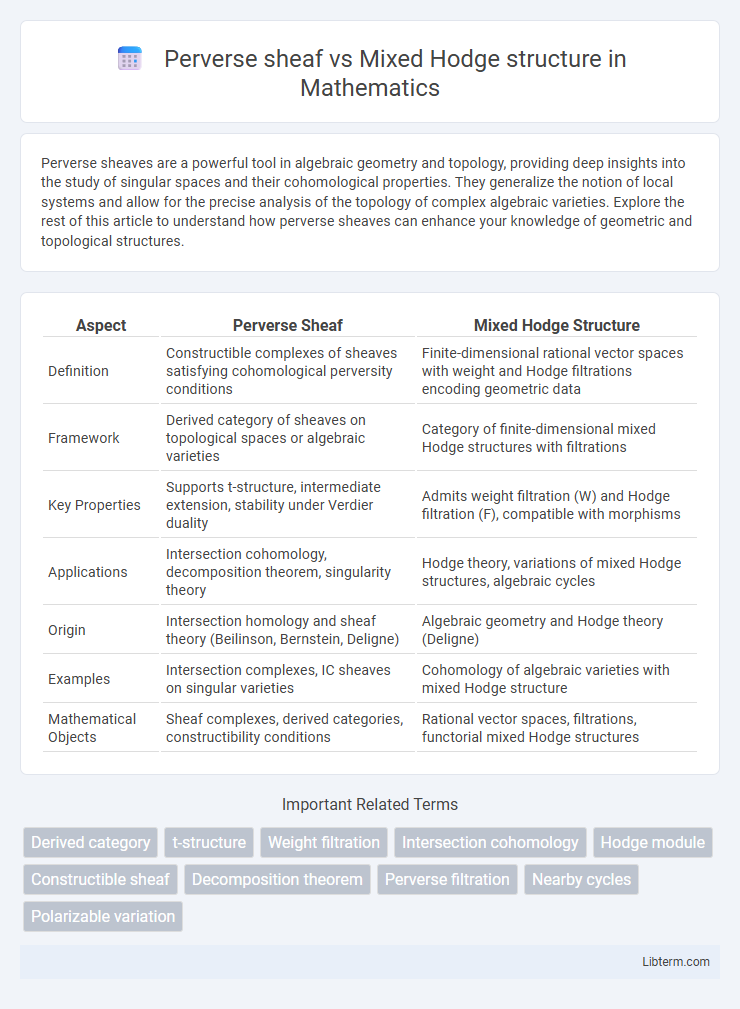
| Aspect | Perverse Sheaf | Mixed Hodge Structure |
|---|---|---|
| Definition | Constructible complexes of sheaves satisfying cohomological perversity conditions | Finite-dimensional rational vector spaces with weight and Hodge filtrations encoding geometric data |
| Framework | Derived category of sheaves on topological spaces or algebraic varieties | Category of finite-dimensional mixed Hodge structures with filtrations |
| Key Properties | Supports t-structure, intermediate extension, stability under Verdier duality | Admits weight filtration (W) and Hodge filtration (F), compatible with morphisms |
| Applications | Intersection cohomology, decomposition theorem, singularity theory | Hodge theory, variations of mixed Hodge structures, algebraic cycles |
| Origin | Intersection homology and sheaf theory (Beilinson, Bernstein, Deligne) | Algebraic geometry and Hodge theory (Deligne) |
| Examples | Intersection complexes, IC sheaves on singular varieties | Cohomology of algebraic varieties with mixed Hodge structure |
| Mathematical Objects | Sheaf complexes, derived categories, constructibility conditions | Rational vector spaces, filtrations, functorial mixed Hodge structures |
Introduction to Perverse Sheaf and Mixed Hodge Structure
Perverse sheaves are intricate objects in algebraic geometry and topology that generalize sheaf cohomology by incorporating singularities and stratifications on complex algebraic varieties. Mixed Hodge structures extend classical Hodge theory by providing a filtration framework that captures the varying degrees of complexity in the cohomology of algebraic varieties, especially those with singularities or non-compact behavior. Both concepts play a crucial role in modern geometric representation theory and the study of singular spaces, offering deep insights into the interplay between topology, algebraic geometry, and arithmetic.
Historical Development of Perverse Sheaves
Perverse sheaves originated in the early 1980s through the work of Goresky and MacPherson, who developed intersection homology to extend Poincare duality to singular spaces. These sheaves formalized a new t-structure on the derived category of sheaves, providing a powerful tool in algebraic geometry and representation theory. The concept laid foundational ground for the Riemann-Hilbert correspondence and influenced the subsequent development of mixed Hodge structures by bridging topology, geometry, and Hodge theory.
Evolution of Mixed Hodge Structures
Mixed Hodge structures evolved as a refinement of classical Hodge theory to capture the intricate interplay between algebraic and topological data in singular or non-compact varieties. Perverse sheaves provide a powerful framework for encoding geometric and cohomological information, facilitating the construction of mixed Hodge modules that bridge perverse sheaves and mixed Hodge structures. The evolution of mixed Hodge structures reflects the integration of derived categories and perverse sheaf theory, enabling deep insights into the decomposition of cohomology and the behavior of singularities.
Key Definitions: Perverse Sheaf
Perverse sheaves are complexes of sheaves on a topological space equipped with a t-structure that generalizes the notion of middle perversity in intersection homology. They encode singularities' topological information through derived category methods, satisfying specific cohomological conditions linked to space stratification. Perverse sheaves play a crucial role in areas such as representation theory, algebraic geometry, and the study of singular spaces.
Key Definitions: Mixed Hodge Structure
Mixed Hodge structures are algebraic objects that generalize pure Hodge structures by incorporating a weight filtration alongside the Hodge filtration, capturing the complexity of singular or non-compact varieties. They consist of a finite-dimensional rational vector space equipped with an increasing weight filtration \(W_\bullet\) and a decreasing Hodge filtration \(F^\bullet\), satisfying compatibility conditions that reflect the geometry and topology of algebraic varieties. Mixed Hodge structures play a crucial role in understanding the cohomological properties of varieties where classical pure Hodge theory does not apply, offering a refined framework for analyzing their mixed Hodge decomposition.
Main Properties and Differences
Perverse sheaves are complexes of sheaves that satisfy specific cohomological conditions related to stratifications, providing a powerful tool for studying singular spaces with applications in intersection cohomology and the decomposition theorem. Mixed Hodge structures introduce filtrations--weight and Hodge filtrations--on cohomology groups, capturing rich geometric and arithmetic information through variations of Hodge structures on singular or non-compact varieties. While perverse sheaves emphasize topological and categorical properties governed by t-structures in derived categories, mixed Hodge structures focus on the linear algebraic data encoding asymptotic behavior and period mappings, linking topology, algebraic geometry, and complex analysis.
Relationship Between Perverse Sheaves and Mixed Hodge Structures
Perverse sheaves provide a powerful framework for categorifying intersection cohomology, while mixed Hodge structures encode refined geometric and topological data on singular varieties. The relationship between perverse sheaves and mixed Hodge structures is established through Saito's theory of mixed Hodge modules, which endows the derived category of perverse sheaves with a natural, functorial mixed Hodge structure. This interplay enhances our understanding of the cohomology of singular spaces by combining topological, algebraic, and Hodge-theoretic invariants in a unified categorical setting.
Applications in Algebraic Geometry and Topology
Perverse sheaves provide a powerful tool for studying singularities in algebraic geometry and the topology of complex algebraic varieties through their deep connection with intersection cohomology, enabling the formulation of the decomposition theorem. Mixed Hodge structures enrich the cohomology groups of algebraic varieties by encoding intricate filtrations reflecting both topological and algebraic information, crucial for understanding variations in Hodge theory and motives. Their interplay facilitates advances in the study of the topology of algebraic maps, singular spaces, and the calculation of characteristic classes, bridging geometric intuition with homological algebra techniques.
Recent Advances in Perverse Sheaves and Mixed Hodge Theory
Recent advances in perverse sheaves highlight deeper connections with mixed Hodge structures through enhanced categorifications and refined t-structures in derived categories. Techniques involving the decomposition theorem and Hodge modules have led to new insights in singularity theory and representation stability. These developments enable more precise computations of Hodge numbers and facilitate the study of intersection cohomology in complex algebraic varieties.
Future Directions and Open Problems
Perverse sheaves and mixed Hodge structures intersect profoundly in complex geometry and representation theory, with future research focusing on their interactions in non-classical settings such as wild ramification and irregular singularities. Open problems include developing a comprehensive theory linking perverse sheaves to mixed Hodge modules in derived categories, which could elucidate deeper arithmetic and geometric properties of singular spaces. Advances in computational methods and categorical frameworks are expected to drive progress in understanding the nuanced behavior of these structures under degeneration and mirror symmetry.
Perverse sheaf Infographic
 libterm.com
libterm.com