A subring is a subset of a ring that itself forms a ring under the same operations of addition and multiplication. It must contain the ring's additive identity and be closed under subtraction and multiplication. Explore the rest of the article to understand how subrings function and why they are essential in algebraic structures.
Table of Comparison
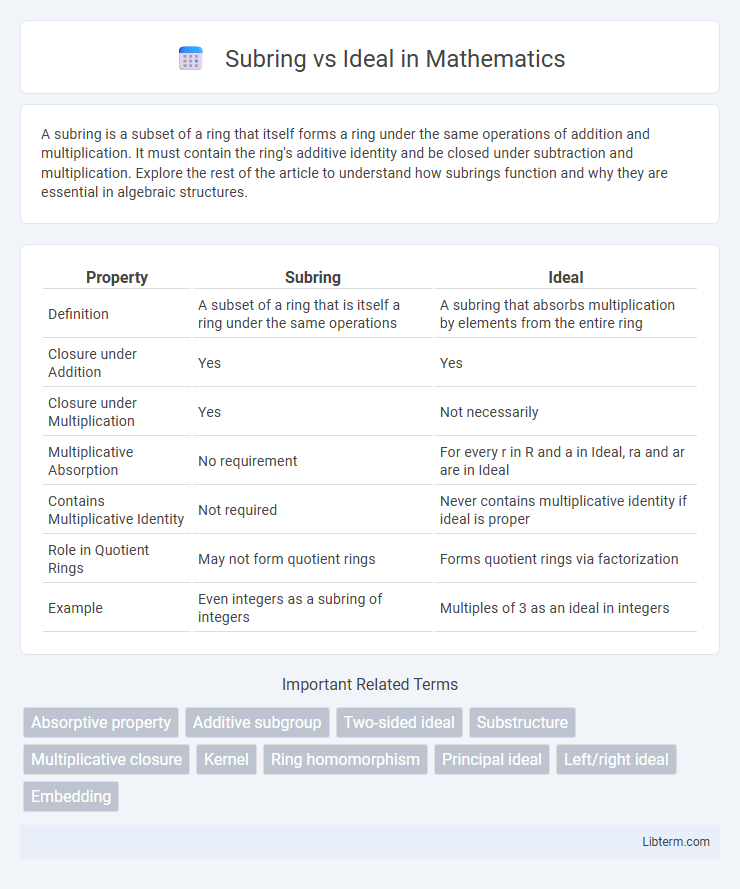
| Property | Subring | Ideal |
|---|---|---|
| Definition | A subset of a ring that is itself a ring under the same operations | A subring that absorbs multiplication by elements from the entire ring |
| Closure under Addition | Yes | Yes |
| Closure under Multiplication | Yes | Not necessarily |
| Multiplicative Absorption | No requirement | For every r in R and a in Ideal, ra and ar are in Ideal |
| Contains Multiplicative Identity | Not required | Never contains multiplicative identity if ideal is proper |
| Role in Quotient Rings | May not form quotient rings | Forms quotient rings via factorization |
| Example | Even integers as a subring of integers | Multiples of 3 as an ideal in integers |
Introduction to Subrings and Ideals
Subrings are subsets of rings that themselves satisfy ring axioms, containing the additive identity and being closed under addition, subtraction, and multiplication. Ideals are special subrings with an absorption property, meaning they absorb multiplication by any element of the larger ring, making them essential in constructing quotient rings. Understanding the distinction between subrings and ideals is fundamental in ring theory, as ideals enable the study of ring homomorphisms and factorization.
Fundamental Definitions: Subring vs Ideal
A subring is a subset of a ring that itself forms a ring under the original operations, containing the additive identity and closed under addition, subtraction, and multiplication. An ideal is a special subring that absorbs multiplication from any element of the parent ring, meaning for any ideal element \( a \) and ring element \( r \), both \( ra \) and \( ar \) belong to the ideal. The fundamental difference lies in ideals serving as kernels of ring homomorphisms and enabling quotient ring construction, whereas subrings need not satisfy this absorption property.
Key Properties of Subrings
Subrings are subsets of a ring that themselves form rings under the same operations, requiring closure under addition, subtraction, and multiplication, and containing the multiplicative identity when the ring is unital. Unlike ideals, subrings do not necessarily absorb multiplication by elements from the entire ring, limiting their role in quotient ring constructions. Key properties of subrings include being closed under ring operations and inheriting the ring's structural features, which makes them fundamental in studying ring homomorphisms and subring lattices.
Essential Characteristics of Ideals
Ideals are special subrings of a ring R that absorb multiplication by any element in R, meaning for any a in R and x in the ideal I, the product ax is also in I; this absorption property distinguishes ideals from general subrings, which need not satisfy this condition. Unlike subrings, ideals serve as kernels of ring homomorphisms and facilitate the construction of quotient rings, making them essential in ring theory and algebraic structures. The requirement that ideals be closed under addition, additive inverses, and absorb multiplication by ring elements formalizes their role in ideal-based factorization and modular arithmetic within rings.
Structure and Formation
A subring is a subset of a ring that itself forms a ring under the same operations, preserving additive and multiplicative closure without requiring absorption by ring elements. An ideal is a special subring that absorbs multiplication by any element from the parent ring, ensuring the product remains within the ideal. The formation of a subring involves closure under addition, subtraction, and multiplication, while an ideal further satisfies the absorption property, making it essential for constructing quotient rings and ring homomorphisms.
Algebraic Differences Between Subrings and Ideals
Subrings are subsets of a ring that are themselves rings, containing the multiplicative identity of the larger ring, and closed under addition, multiplication, and additive inverses. Ideals are special subsets of rings that absorb multiplication from elements in the whole ring, ensuring that any product of an element in the ideal with an element in the ring remains inside the ideal. Unlike subrings, ideals serve as kernels of ring homomorphisms and are crucial for constructing quotient rings, highlighting their role in ring theory and algebraic structure.
Examples Illustrating Subrings
Examples illustrating subrings include the set of all even integers within the ring of integers, demonstrating closure under addition and multiplication while containing the additive identity. Another example is the collection of all 2x2 upper triangular matrices within the ring of 2x2 matrices over a field, confirming subring properties through matrix addition and multiplication. These instances highlight subrings as subsets maintaining ring operations without necessarily absorbing multiplication from the larger ring, a key distinction from ideals.
Examples Demonstrating Ideals
Ideals in ring theory, such as the set of even integers within the ring of integers, serve as foundational examples distinguishing them from subrings, which need not absorb multiplication by arbitrary ring elements. For instance, the ideal \(2\mathbb{Z}\) includes all multiples of 2 and fulfills absorption under multiplication, whereas the subring of integers congruent to 1 modulo 3 is closed under addition and multiplication but is not an ideal. These examples illustrate how ideals function as kernels of ring homomorphisms, critical in constructing quotient rings and analyzing ring structure.
Applications in Abstract Algebra
Subrings and ideals serve distinct roles in abstract algebra, with subrings providing a framework for studying smaller, self-contained algebraic structures within a ring, essential for understanding ring homomorphisms and factorization. Ideals are critical for constructing quotient rings, enabling the analysis of ring properties via kernel analysis and facilitating the classification of rings through prime and maximal ideals. Applications of ideals are particularly pivotal in algebraic geometry and number theory, where they help describe solution sets of polynomial equations and enable the formulation of ring-theoretic analogs of division.
Comparing Subrings and Ideals: A Summary
Subrings are subsets of rings that contain the multiplicative identity and are closed under addition, subtraction, and multiplication, whereas ideals are special subrings that absorb multiplication by any element of the parent ring. Unlike subrings, ideals are crucial for constructing quotient rings and play a fundamental role in ring homomorphisms and factorization. The main difference lies in ideals meeting the absorption property, making them essential for defining kernels and facilitating algebraic structures in abstract algebra.
Subring Infographic
 libterm.com
libterm.com