Spectral sequence differentials capture the transitions between pages in a spectral sequence, revealing complex algebraic structures through successive approximations. Understanding these differentials allows you to compute homology or cohomology groups by interpreting how cycles and boundaries evolve across layers. Dive into the rest of the article to explore the role and computation of spectral sequence differentials in greater detail.
Table of Comparison
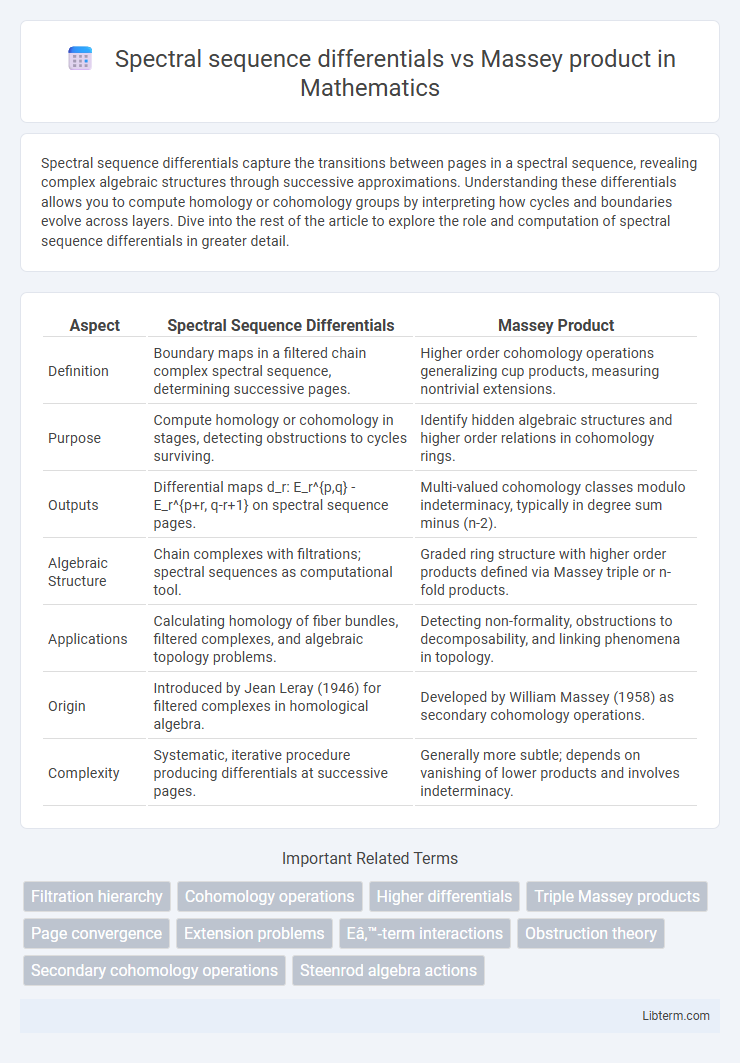
| Aspect | Spectral Sequence Differentials | Massey Product |
|---|---|---|
| Definition | Boundary maps in a filtered chain complex spectral sequence, determining successive pages. | Higher order cohomology operations generalizing cup products, measuring nontrivial extensions. |
| Purpose | Compute homology or cohomology in stages, detecting obstructions to cycles surviving. | Identify hidden algebraic structures and higher order relations in cohomology rings. |
| Outputs | Differential maps d_r: E_r^{p,q} - E_r^{p+r, q-r+1} on spectral sequence pages. | Multi-valued cohomology classes modulo indeterminacy, typically in degree sum minus (n-2). |
| Algebraic Structure | Chain complexes with filtrations; spectral sequences as computational tool. | Graded ring structure with higher order products defined via Massey triple or n-fold products. |
| Applications | Calculating homology of fiber bundles, filtered complexes, and algebraic topology problems. | Detecting non-formality, obstructions to decomposability, and linking phenomena in topology. |
| Origin | Introduced by Jean Leray (1946) for filtered complexes in homological algebra. | Developed by William Massey (1958) as secondary cohomology operations. |
| Complexity | Systematic, iterative procedure producing differentials at successive pages. | Generally more subtle; depends on vanishing of lower products and involves indeterminacy. |
Introduction to Spectral Sequences and Massey Products
Spectral sequence differentials provide a powerful computational tool for approximating the homology or cohomology of filtered complexes, revealing successive approximations to the target object through pages E_r and differentials d_r. Massey products, higher-order cohomology operations, detect nontrivial extensions and hidden relations not captured by primary cohomology operations, offering deep insight into algebraic structures. Understanding the interplay between spectral sequence differentials and Massey products is crucial for unraveling complex algebraic topology phenomena, where spectral sequences help organize computations and Massey products reveal nuanced algebraic interactions.
Foundations: Understanding Differentials in Spectral Sequences
Differentials in spectral sequences are homomorphisms that reveal hidden extensions and guide convergence to target homology or cohomology groups, characterized by their degree and filtration shifts. Massey products, higher-order cohomological operations, detect intricate algebraic structures not visible through primary differentials but can correspond to obstructions arising in successive pages of spectral sequences. Foundational understanding of spectral sequence differentials involves recognizing their role in systematically approximating complex invariants, while Massey products provide complementary insights into nontrivial product structures and extension problems in algebraic topology.
Defining Massey Products in Cohomology
Massey products in cohomology generalize cup products by capturing higher-order interactions among cohomology classes, providing information beyond the classical ring structure. Spectral sequence differentials often detect obstructions related to the indeterminacy of Massey products, linking filtrations in spectral sequences to these higher-order cohomological operations. Defining Massey products involves constructing cochains whose coboundaries correspond to cup products of given classes, with nontrivial Massey products indicating hidden extensions or linking phenomena in the cohomology algebra.
Algebraic Structures: Bridging Spectral Sequences and Massey Products
Spectral sequence differentials encode complex algebraic relationships that reflect hidden extensions within filtered chain complexes, while Massey products capture higher-order cohomological operations revealing nontrivial linking between classes. Both tools elucidate intricate algebraic structures in homological algebra and algebraic topology, with differentials detecting obstructions in spectral filtrations and Massey products representing multi-valued operations that generalize the cup product. Their interplay enables a deeper understanding of algebraic invariants, linking spectral sequence convergence properties to secondary operations characterized by Massey products.
Key Differences Between Spectral Sequence Differentials and Massey Products
Spectral sequence differentials are algebraic maps that compute successive approximations to homology or cohomology groups, while Massey products are higher-order cohomology operations capturing nontrivial relations between cohomology classes. Differentials operate within a graded chain complex structure, providing boundary maps between pages of a spectral sequence, whereas Massey products reveal hidden algebraic structures and obstructions not detected by ordinary products. The key difference lies in their roles: spectral sequence differentials progressively refine homological information, whereas Massey products detect intricate higher-order interactions in the cohomology ring.
Geometric and Topological Insights: Interpretations and Examples
Spectral sequence differentials reveal hidden algebraic structures by tracking the failure of exactness across filtration levels, while Massey products detect higher-order cohomological relations unresolved by cup products, offering refined invariants in topology. In geometric contexts, differentials relate to boundary maps in filtered complexes, capturing subtle geometric transitions, whereas Massey products often correspond to linking phenomena or obstructions in extending cohomological classes. For example, in the study of link complements, spectral sequence differentials encode iterative intersection data, while Massey products provide explicit measures of triple linking numbers, highlighting nuanced topological complexities.
Computational Techniques for Detecting Higher Order Structures
Spectral sequence differentials provide an algorithmic framework for computing successive approximations to homology groups, revealing hidden extensions and obstructions in filtered complexes. Massey products capture higher order cohomology operations that detect intricate algebraic structures beyond ordinary cup products, offering insight into nontrivial linking phenomena. Computational techniques leverage spectral sequence convergence and Massey product algorithms, such as combinatorial chain-level methods and homotopy transfer, to systematically identify and analyze higher order structures in algebraic topology and homological algebra.
Interplay and Applications in Algebraic Topology
Spectral sequence differentials and Massey products interact deeply in algebraic topology by providing complementary tools to detect hidden extensions and higher-order structures in cohomology. The differentials in spectral sequences reveal filtration-induced relationships, while Massey products capture nontrivial triple or higher cohomology operations that escape classical cup product detection. This interplay is crucial for analyzing the structure of loop spaces, classifying fiber bundles, and resolving ambiguities in Postnikov towers.
Recent Developments and Research Directions
Recent developments in spectral sequence differentials have highlighted intricate interactions with Massey products, revealing deeper insights into higher-order cohomological operations and obstruction theories. Cutting-edge research employs homotopical and algebraic techniques to systematically compute differentials via Massey product structures, advancing the understanding of filtrations in complex topological spaces. Emerging directions focus on leveraging these connections to classify stable homotopy groups and refine computational frameworks in derived algebraic geometry.
Conclusion: Implications and Future Perspectives
Spectral sequence differentials provide a systematic approach to unraveling complex homological information, while Massey products reveal higher-order cohomology operations capturing subtle algebraic structures beyond primary differentials. The interplay between these tools enhances our understanding of the obstructions and extensions in algebraic topology and homological algebra, suggesting new avenues for classifying complicated topological spaces. Future research may focus on developing computational techniques to explicitly relate spectral sequence differentials and Massey products, potentially advancing the study of deformation theory and homotopy types.
Spectral sequence differentials Infographic
 libterm.com
libterm.com