The Hausdorff Maximal Principle states that in any partially ordered set, every chain (totally ordered subset) can be extended to a maximal chain. This principle is crucial in set theory and has applications in topology, algebra, and logic, helping to establish the existence of maximal elements under certain conditions. Explore the rest of this article to understand how the Hausdorff Maximal Principle influences various mathematical fields and its connections to other fundamental axioms.
Table of Comparison
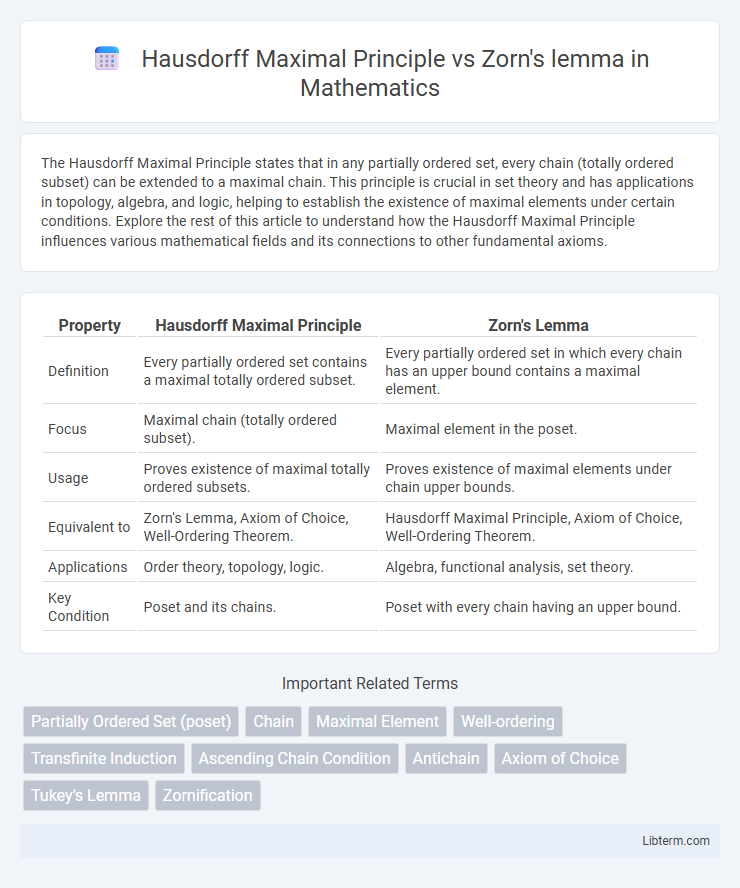
| Property | Hausdorff Maximal Principle | Zorn's Lemma |
|---|---|---|
| Definition | Every partially ordered set contains a maximal totally ordered subset. | Every partially ordered set in which every chain has an upper bound contains a maximal element. |
| Focus | Maximal chain (totally ordered subset). | Maximal element in the poset. |
| Usage | Proves existence of maximal totally ordered subsets. | Proves existence of maximal elements under chain upper bounds. |
| Equivalent to | Zorn's Lemma, Axiom of Choice, Well-Ordering Theorem. | Hausdorff Maximal Principle, Axiom of Choice, Well-Ordering Theorem. |
| Applications | Order theory, topology, logic. | Algebra, functional analysis, set theory. |
| Key Condition | Poset and its chains. | Poset with every chain having an upper bound. |
Introduction to the Hausdorff Maximal Principle and Zorn's Lemma
The Hausdorff Maximal Principle asserts that every partially ordered set contains a maximal totally ordered subset, emphasizing the existence of maximal chains within the set. Zorn's Lemma states that a partially ordered set in which every chain has an upper bound contains at least one maximal element, serving as a fundamental tool in various areas of algebra and topology. Both principles are equivalent formulations of the Axiom of Choice and play crucial roles in set theory and functional analysis.
Historical Context and Development
The Hausdorff Maximal Principle, formulated by Felix Hausdorff in 1914, emerged from early set theory and aimed to establish maximal elements in partially ordered sets. Zorn's lemma, introduced by Max Zorn in 1935, built upon earlier work including Hausdorff's and became pivotal in modern algebra and functional analysis for proving the existence of maximal elements. Both principles are equivalent to the Axiom of Choice, reflecting foundational developments in set theory throughout the early 20th century.
Formal Definitions: Hausdorff Maximal Principle
The Hausdorff Maximal Principle states that in any partially ordered set, every chain is contained in a maximal chain, emphasizing the existence of maximal totally ordered subsets. Formally, for a partially ordered set (P, <=), there exists a chain C P such that no chain strictly contains C. This principle is equivalent to Zorn's lemma and is instrumental in proofs requiring maximal elements under specific orderings.
Formal Definitions: Zorn's Lemma
Zorn's Lemma states that a partially ordered set in which every chain has an upper bound contains at least one maximal element. Formally, if \( (P, \leq) \) is a partially ordered set and every totally ordered subset \( C \subseteq P \) has an upper bound in \( P \), then there exists a maximal element \( m \in P \) such that no element \( p \in P \) satisfies \( m < p \). This principle is fundamental in set theory and is equivalent to the Axiom of Choice.
Mathematical Relationships and Equivalence
Hausdorff Maximal Principle asserts that every partially ordered set contains a maximal totally ordered subset, while Zorn's Lemma states that any partially ordered set in which every chain has an upper bound contains a maximal element. Both principles are equivalent formulations within the framework of Zermelo-Fraenkel set theory with the Axiom of Choice, underpinning the existence of maximal elements under certain conditions. Their equivalence highlights the foundational role they play in various mathematical proofs involving maximality and order theory.
Illustrative Examples and Applications
Hausdorff Maximal Principle is exemplified by the construction of maximal chains in partially ordered sets, such as selecting a maximal totally ordered subset of a given set, pivotal in order theory and topology. Zorn's Lemma is widely applied in algebra, for instance, proving every vector space has a basis by asserting the existence of maximal linearly independent subsets. Both principles are equivalent formulations of the Axiom of Choice, with Hausdorff Maximal Principle better suited for chain-based arguments, while Zorn's Lemma is preferred in establishing maximal elements in partially ordered structures like ideals in rings or spanning sets in vector spaces.
Comparative Analysis: Strengths and Weaknesses
The Hausdorff Maximal Principle guarantees the existence of maximal elements in partially ordered sets by asserting that every chain has an upper bound, making it particularly useful in constructive arguments involving linear orders. Zorn's Lemma, stronger in scope, applies to more general partially ordered sets by ensuring maximal elements when every chain has an upper bound, widely used in algebra and functional analysis to prove existence theorems. While Hausdorff's principle is more intuitive and easier to visualize, Zorn's Lemma offers broader applicability but often requires the Axiom of Choice, which can introduce non-constructive elements in proofs.
Role in Modern Set Theory and Mathematics
Hausdorff Maximal Principle and Zorn's Lemma are equivalent forms of the Axiom of Choice, pivotal in modern set theory and abstract algebra. Zorn's Lemma is extensively used to prove the existence of maximal elements in partially ordered sets, facilitating key results in vector space theory, ring theory, and module theory. Hausdorff Maximal Principle emphasizes the existence of maximal chains, playing a crucial role in the analysis of well-orderings and is instrumental in the development of order theory and lattice theory.
Common Misconceptions and Clarifications
Hausdorff Maximal Principle and Zorn's Lemma are often mistakenly viewed as entirely distinct concepts, while both are equivalent formulations of the Axiom of Choice in set theory. A common misconception is that Hausdorff Maximal Principle applies only to chains in partially ordered sets and Zorn's Lemma only to maximal elements, but both statements fundamentally address the existence of maximal elements under certain conditions. Clarifying their equivalence helps avoid confusion in proofs, as both principles guarantee maximality but are applied differently depending on the structure of the set and order relation involved.
Conclusion and Further Reading
Hausdorff Maximal Principle and Zorn's Lemma are equivalent formulations in set theory, both crucial for proving the existence of maximal elements in partially ordered sets. Their equivalence highlights foundational aspects of the Axiom of Choice, underpinning many mathematical theories in algebra and topology. For deeper exploration, consult foundational texts like Jech's "Set Theory" and Kunen's "The Foundations of Mathematics.
Hausdorff Maximal Principle Infographic
 libterm.com
libterm.com