A free group is a fundamental concept in abstract algebra characterized by a set of elements with no relations apart from the group axioms, allowing unrestricted combination of its generators. It plays a crucial role in various fields like topology, algebraic geometry, and combinatorial group theory. Discover how understanding free groups can deepen your grasp of mathematical structures in the rest of this article.
Table of Comparison
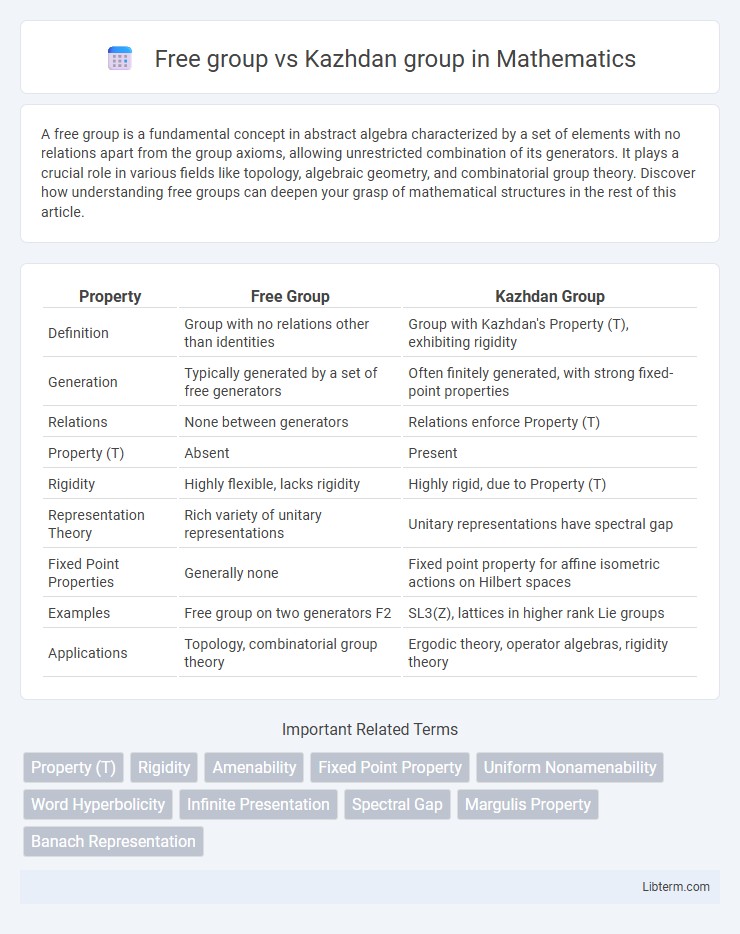
| Property | Free Group | Kazhdan Group |
|---|---|---|
| Definition | Group with no relations other than identities | Group with Kazhdan's Property (T), exhibiting rigidity |
| Generation | Typically generated by a set of free generators | Often finitely generated, with strong fixed-point properties |
| Relations | None between generators | Relations enforce Property (T) |
| Property (T) | Absent | Present |
| Rigidity | Highly flexible, lacks rigidity | Highly rigid, due to Property (T) |
| Representation Theory | Rich variety of unitary representations | Unitary representations have spectral gap |
| Fixed Point Properties | Generally none | Fixed point property for affine isometric actions on Hilbert spaces |
| Examples | Free group on two generators F2 | SL3(Z), lattices in higher rank Lie groups |
| Applications | Topology, combinatorial group theory | Ergodic theory, operator algebras, rigidity theory |
Understanding Free Groups: Definitions and Properties
Free groups are algebraic structures generated by a set of elements where no relations exist other than those necessary to satisfy group axioms, ensuring every element can be uniquely represented as a reduced word. These groups serve as fundamental building blocks in group theory, characterized by their universal mapping property and infinite, non-abelian nature when generated by two or more elements. Understanding free groups involves recognizing their role in constructing and analyzing more complex groups, including Kazhdan groups, which impose rigidity properties starkly contrasting the free group's inherent freedom.
Overview of Kazhdan’s Property (T)
Kazhdan's Property (T) is a rigidity property for topological groups that ensures every unitary representation with almost invariant vectors has an invariant vector, leading to strong fixed-point properties. Free groups, characterized by their lack of relations and hyperbolic behavior, do not have Property (T) and exhibit high degrees of freedom and flexibility. Kazhdan groups, often arising from lattices in higher-rank Lie groups, demonstrate strong spectral gaps and rapid decay of matrix coefficients, enabling applications in ergodic theory, operator algebras, and geometric group theory.
Key Differences Between Free Groups and Kazhdan Groups
Free groups are defined by having a basis where every element can be uniquely represented as a reduced word without relations, exhibiting properties like infinite dimensionality and non-amenability. Kazhdan groups, characterized by Kazhdan's Property (T), possess strong rigidity properties and have a spectral gap that implies fixed point properties for unitary representations. The key differences lie in structural flexibility, where free groups lack Property (T) and are highly non-rigid, while Kazhdan groups have constrained representations, making them more resistant to deformations and group actions.
Structural Characteristics of Free Groups
Free groups are characterized by a set of generators with no relations other than the identity, resulting in a highly non-abelian and infinitely generated structure. Their Cayley graphs form infinite trees, reflecting the absence of cycles and enabling unique reduced word representations for each group element. This fundamental combinatorial rigidity contrasts with Kazhdan groups, where property (T) imposes strong constraints on representations and tends to foster rigidity and fixed-point properties in unitary actions.
Core Features of Kazhdan (Property T) Groups
Kazhdan groups, characterized by Property T, exhibit strong rigidity properties that enforce fixed points for any affine isometric action on Hilbert spaces, distinguishing them significantly from free groups known for their high degree of flexibility and lack of such fixed point properties. Core features of Kazhdan groups include spectral gaps in their unitary representations, ensuring rapid convergence in random walks and robust resistance to deformation. These groups also display limited amenability and enhanced structural stability, making them central in fields such as geometric group theory and operator algebras.
Representation Theory in Free and Kazhdan Groups
Free groups exhibit rich and highly flexible unitary representations, often characterized by abundant infinite-dimensional irreducible representations reflecting their non-amenability and lack of spectral gaps. Kazhdan groups, defined by Property (T), have strong rigidity in their representation theory, ensuring that every unitary representation with almost invariant vectors contains invariant vectors, leading to fixed point properties and spectral gaps in the associated unitary representations. This fundamental difference in representation theory impacts ergodic theory, operator algebras, and geometric group theory, with Kazhdan groups yielding robust spectral and rigidity phenomena absent in free groups.
Amenability: Contrasting Behaviors
Free groups are non-amenable, characterized by their exponential growth and lack of invariant means, which makes them central examples in geometric group theory demonstrating non-amenability. Kazhdan groups, possessing property (T), exhibit strong rigidity and fixed-point properties that enforce amenability constraints in various contexts, particularly in ergodic theory and operator algebras. The contrasting amenability behavior between free groups and Kazhdan groups highlights fundamental differences in algebraic and analytical properties, influencing their applications in harmonic analysis and representation theory.
Examples and Non-Examples of Each Group Type
Free groups are exemplified by groups like the free group on two generators, often denoted F_2, characterized by their lack of relations other than the group axioms, making them highly non-amenable and without property (T). Kazhdan groups, such as SL(3, Z) or lattices in higher-rank Lie groups, possess Kazhdan's property (T), implying strong rigidity and fixed-point properties absent in free groups. Non-examples include free abelian groups, which lack property (T) and thus are not Kazhdan groups, and certain infinite simple groups that do not exhibit the freedom of free groups or the rigidity of Kazhdan groups.
Applications in Modern Mathematics and Physics
Free groups serve as foundational models in algebraic topology and geometric group theory, enabling the study of space symmetries and automorphisms in discrete systems. Kazhdan groups, characterized by property (T), play a critical role in rigidity phenomena, spectral gap problems, and expander graph construction with applications in quantum computing and condensed matter physics. Both structures influence representation theory and ergodic theory, shaping advances in understanding symmetry, randomness, and stability in mathematical physics.
Open Problems and Research Directions
Open problems in the study of free groups versus Kazhdan groups involve understanding how Kazhdan's property (T) influences rigidity and representation theory compared to the flexible structure of free groups. Research explores the boundary between these groups in geometric group theory, focusing on characterizing groups with intermediate properties or mixed behaviors. Advances in analytical methods and ergodic theory continue to shape directions towards resolving questions about spectral gaps, cohomology, and the classification of groups with property (T).
Free group Infographic
 libterm.com
libterm.com