Graded modules extend the concept of modules by incorporating a grading structure that aligns elements with specific degrees, enabling refined algebraic analysis. This structure facilitates the study of homological properties and interactions within graded rings, offering deeper insights into algebraic geometry and representation theory. Explore the article to understand how graded modules can enhance your mathematical framework and problem-solving approach.
Table of Comparison
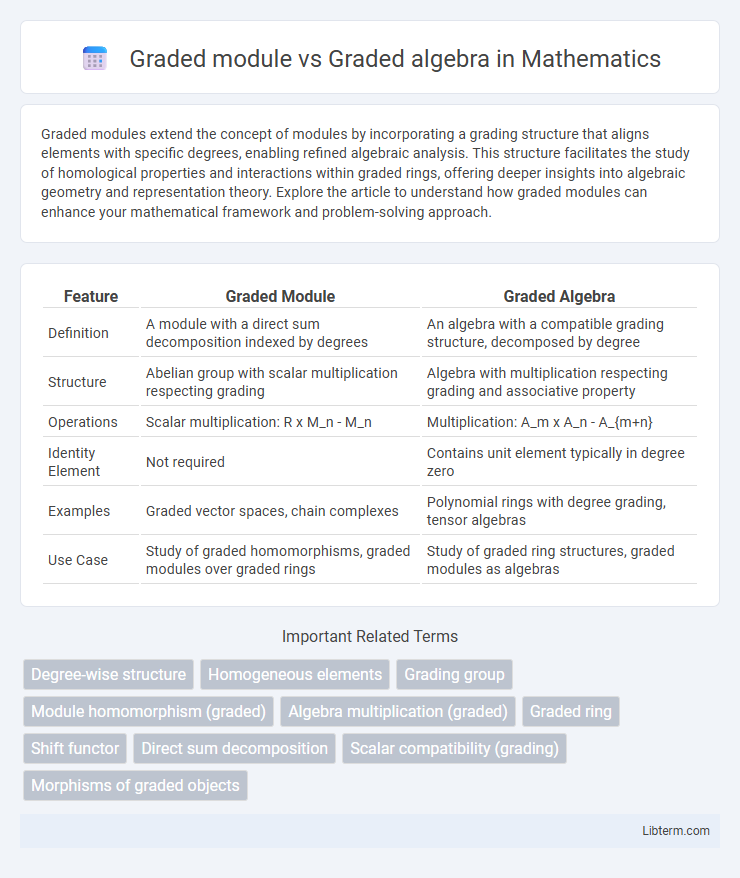
| Feature | Graded Module | Graded Algebra |
|---|---|---|
| Definition | A module with a direct sum decomposition indexed by degrees | An algebra with a compatible grading structure, decomposed by degree |
| Structure | Abelian group with scalar multiplication respecting grading | Algebra with multiplication respecting grading and associative property |
| Operations | Scalar multiplication: R x M_n - M_n | Multiplication: A_m x A_n - A_{m+n} |
| Identity Element | Not required | Contains unit element typically in degree zero |
| Examples | Graded vector spaces, chain complexes | Polynomial rings with degree grading, tensor algebras |
| Use Case | Study of graded homomorphisms, graded modules over graded rings | Study of graded ring structures, graded modules as algebras |
Introduction to Graded Structures
Graded modules are algebraic structures composed of a direct sum of submodules indexed by a grading set, typically the integers, allowing elements to be tracked by their degree. Graded algebras extend this concept by incorporating a compatible multiplication operation that respects the grading, enabling the product of elements to align with the sum of their degrees. These graded structures play a fundamental role in homological algebra, representation theory, and algebraic geometry, providing a framework for analyzing complex algebraic objects through their graded components.
Defining Graded Modules
A graded module is a module decomposed into a direct sum of abelian groups indexed by a grading set, typically the integers, enabling the study of elements by their degree. Each graded component respects the module operations, allowing homomorphisms and submodules to preserve grading structure. In contrast, a graded algebra is a graded module with a compatible multiplication operation that respects the grading, forming a richer algebraic structure.
Understanding Graded Algebras
Graded algebras are algebraic structures equipped with a decomposition into a direct sum of submodules indexed by a grading set, typically the non-negative integers, where the multiplication respects the grading by mapping elements of degree m and n to degree m + n. Understanding graded algebras involves recognizing how the graded components interact multiplicatively to preserve structure, unlike graded modules which only require a compatible grading without multiplicative closure. Applications in algebraic geometry, homological algebra, and representation theory highlight the importance of graded algebras in encoding additional symmetries and hierarchical information through their graded structure.
Key Differences: Graded Module vs Graded Algebra
Graded modules consist of a collection of abelian groups indexed by a grading set, typically integers, where module operations respect the grading but lack an internal multiplication operation. Graded algebras extend graded modules by incorporating a compatible graded multiplication, making the algebra structure both graded and associative with identity elements in some cases. The fundamental difference lies in graded algebras having a bilinear graded multiplication map, whereas graded modules only support scalar multiplication from an underlying ring or algebra without graded product closure.
Structures and Operations in Graded Modules
Graded modules consist of a direct sum decomposition M = _n M_n over a ring, where each component M_n is an abelian group and scalar multiplication respects the grading. Graded algebras extend graded modules by incorporating a graded multiplication operation A_m x A_n - A_{m+n} that is associative and distributive, creating additional algebraic structures. In graded modules, operations focus on addition and scalar multiplication within each graded component, while in graded algebras, the multiplication operation combines elements across grades, enriching the structure with both additive and multiplicative properties.
Algebraic Properties Unique to Graded Algebras
Graded algebras possess a multiplication operation that respects the grading, meaning the product of elements from two graded components lies in the component indexed by the sum of their grades, a property absent in graded modules. This graded multiplication induces a richer algebraic structure allowing for the formulation of graded ideals, homomorphisms, and graded morphisms that preserve both the module structure and the grading. The presence of a unit element that is homogeneous of degree zero further distinguishes graded algebras, enabling constructions like graded polynomial rings and graded tensor algebras essential in homological algebra and algebraic geometry.
Examples Illustrating Graded Modules
Graded modules generalize vector spaces by decomposing into direct sums indexed by degrees, such as $\mathbb{Z}$-graded modules over polynomial rings like $k[x]$, where each graded component corresponds to homogeneous polynomials of fixed degree. In contrast, graded algebras possess both graded module structure and multiplication compatible with grading, exemplified by the polynomial ring $k[x]$ graded by degree. Examples illustrating graded modules include chain complexes in homological algebra, where each chain group forms a graded component, and modules over the exterior algebra graded by form degree, emphasizing the role of grading in homomorphisms and submodule structures.
Examples Illustrating Graded Algebras
Graded algebras encompass examples such as polynomial rings with degrees assigned to variables, where the algebraic structure is decomposed into homogeneous components combining via multiplication. Another illustrative example is the exterior algebra generated by a vector space, graded by the degree of wedge products, which plays a pivotal role in differential geometry and topology. Unlike graded modules that only have graded additive structures, graded algebras incorporate both graded addition and graded multiplication, enabling richer algebraic operations indexed by degrees.
Interconnection Between Graded Modules and Algebras
Graded modules and graded algebras share a structural hierarchy where graded modules serve as modules over graded algebras, preserving degree-based decompositions that maintain algebraic consistency. The interconnection is pivotal in homological algebra and algebraic geometry, as graded algebras act as rings with an intrinsic grading that induces corresponding graded module structures, facilitating the study of syzygies and resolutions. This relationship enriches the understanding of module operations and morphisms within a graded context, enabling deeper insights into algebraic invariants and category theory frameworks.
Applications and Significance in Mathematics
Graded modules, structured as modules with a decomposition compatible with scalar multiplication, play a critical role in homological algebra and representation theory by enabling the study of filtered objects and spectral sequences. Graded algebras extend this structure by incorporating a compatible multiplication, making them indispensable in algebraic geometry, where they describe projective varieties via graded rings, and in topology, specifically in cohomology rings of graded spaces. Both concepts facilitate the analysis of algebraic and geometric structures by encoding degree-based symmetries essential for computational methods and theoretical frameworks in modern mathematics.
Graded module Infographic
 libterm.com
libterm.com