A Riesz basis is a sequence of elements in a Hilbert space that is complete and allows stable, unique representations of any vector in that space, generalizing the concept of an orthonormal basis. These bases are crucial in functional analysis and signal processing because they enable efficient and robust decompositions despite not being orthogonal. Explore the article to understand how a Riesz basis can optimize your work with complex vector spaces.
Table of Comparison
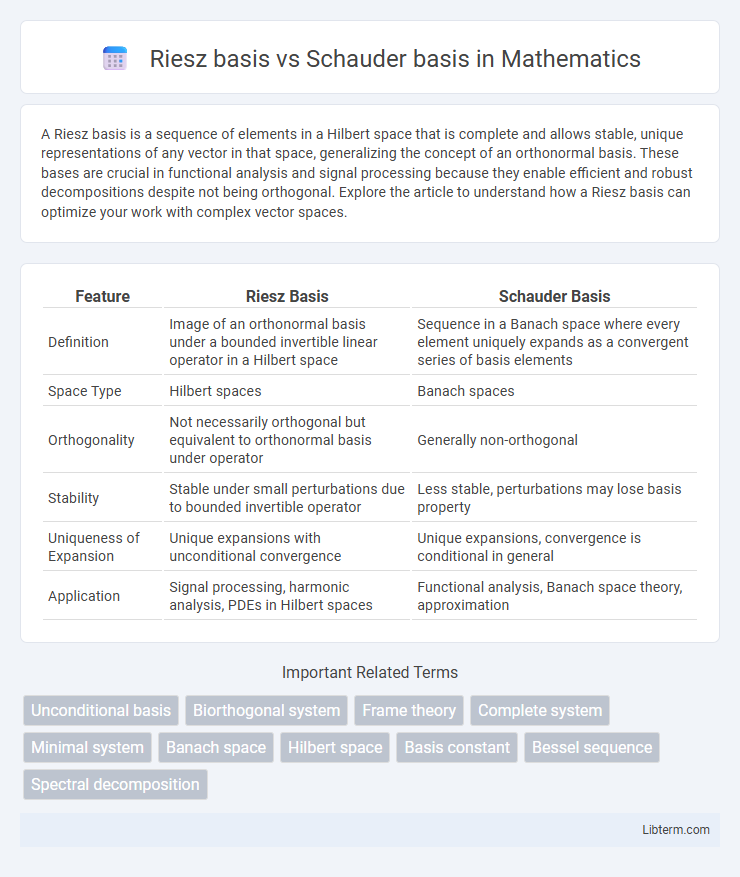
| Feature | Riesz Basis | Schauder Basis |
|---|---|---|
| Definition | Image of an orthonormal basis under a bounded invertible linear operator in a Hilbert space | Sequence in a Banach space where every element uniquely expands as a convergent series of basis elements |
| Space Type | Hilbert spaces | Banach spaces |
| Orthogonality | Not necessarily orthogonal but equivalent to orthonormal basis under operator | Generally non-orthogonal |
| Stability | Stable under small perturbations due to bounded invertible operator | Less stable, perturbations may lose basis property |
| Uniqueness of Expansion | Unique expansions with unconditional convergence | Unique expansions, convergence is conditional in general |
| Application | Signal processing, harmonic analysis, PDEs in Hilbert spaces | Functional analysis, Banach space theory, approximation |
Introduction to Basis Concepts in Functional Analysis
In functional analysis, a Riesz basis is a complete system in a Hilbert space that is the image of an orthonormal basis under a bounded invertible operator, ensuring both completeness and stability of expansions. A Schauder basis, defined in general Banach spaces, allows unique representation of every element as a convergent series but may lack the orthogonality and norm equivalence properties found in Riesz bases. Understanding the distinction between these bases highlights their roles in approximation theory and spectral analysis, where Riesz bases provide robust reconstruction similar to orthonormal systems, whereas Schauder bases offer broader applicability in non-Hilbertian settings.
Defining Schauder Basis: Fundamentals and Properties
A Schauder basis in a Banach space is a sequence \((x_n)\) such that every element in the space can be uniquely represented as a convergent series \(\sum a_n x_n\) with scalar coefficients \(a_n\). Unlike a Riesz basis, which is an orthonormal basis under an equivalent inner product and inherits Hilbert space structure, a Schauder basis does not require orthogonality or norm equivalence. Key properties include unconditional convergence in some cases and the ability to define coordinate functionals that are continuous linear maps associated with the basis.
Understanding Riesz Basis: Formal Definition and Key Traits
A Riesz basis in a Hilbert space is a sequence of vectors obtained by applying a bounded, invertible linear operator to an orthonormal basis, preserving completeness and allowing stable, unique representations of elements. Unlike a general Schauder basis, which ensures unique expansion but may lack stability or norm equivalence, a Riesz basis guarantees norm equivalence between the sequence coefficients and the Hilbert space norm. Key traits of a Riesz basis include biorthogonality with bounded frame bounds and robustness under perturbations, making it fundamental for applications in functional analysis and signal processing.
Historical Development of Riesz and Schauder Bases
Riesz bases were introduced by Frigyes Riesz in the early 20th century as a refinement of orthonormal bases to accommodate stable expansions in Hilbert spaces, emphasizing the preservation of norm equivalences. Schauder bases, named after Juliusz Schauder, emerged from studies in Banach spaces with a focus on series expansions allowing unique representations even without orthogonality. The historical development of these bases reflects the evolution from rigid orthonormal frameworks to more flexible, yet stable, structures in functional analysis, bridging gaps between Hilbert and Banach space theories.
Structural Differences Between Riesz Basis and Schauder Basis
A Riesz basis is a sequence in a Hilbert space that is the image of an orthonormal basis under a bounded invertible linear operator, ensuring both completeness and stability with norm equivalences. In contrast, a Schauder basis only requires that every element in the Banach space can be uniquely represented as a norm-convergent series of basis elements, lacking the inherent orthogonality and stability properties of a Riesz basis. Structural differences lie in the Riesz basis's tight norm bounds and biorthogonal system, while the Schauder basis depends solely on convergence and uniqueness without guaranteeing uniform boundedness of the basis projections.
Characterizations and Examples in Hilbert and Banach Spaces
Riesz bases in Hilbert spaces are characterized by sequences that are the image of an orthonormal basis under a bounded, invertible operator, ensuring stability and unique expansions similar to orthonormal bases. Schauder bases in Banach spaces generalize this concept by providing unique expansions without requiring orthogonality or isometric properties, often characterized by the boundedness of coordinate projections. Examples include the exponential system forming a Riesz basis in \(L^2\) spaces and the canonical basis in \(\ell^p\) spaces serving as Schauder bases in corresponding Banach spaces.
Conditions for a Schauder Basis to Be a Riesz Basis
A Schauder basis in a Hilbert space becomes a Riesz basis if it is both complete and equivalent to an orthonormal basis under a bounded invertible linear operator. This condition guarantees uniform boundedness of the basis projections and the existence of biorthogonal functionals with stable norms. Consequently, the basis sequences must satisfy the frame condition, ensuring stability and robustness similar to orthonormal bases in terms of convergence and expansion.
Applications and Significance in Mathematical Analysis
Riesz bases provide a stable and robust framework ideal for signal processing, harmonic analysis, and quantum mechanics due to their similarity to orthonormal bases combined with flexibility in non-orthogonal expansions. Schauder bases, fundamental for Banach space theory, enable representation of elements through convergent series, crucial in approximation theory, functional analysis, and solving operator equations. The significance of Riesz bases lies in their complete and unconditional properties that facilitate numerical stability, while Schauder bases are pivotal in studying general topological vector spaces and nonlinear analysis.
Advantages and Limitations of Riesz vs. Schauder Bases
Riesz bases provide the advantage of stability and unconditional convergence in Hilbert spaces, ensuring robust and efficient signal reconstruction due to their orthonormal-like properties. Schauder bases, while more general and applicable in Banach spaces, often lack unconditional convergence, leading to potential instability in representations. The limitation of Riesz bases lies in their restriction to Hilbert spaces, whereas Schauder bases' broader scope comes at the cost of weaker structural guarantees and potential computational complexity.
Conclusion: Choosing the Right Basis for Functional Analysis
Riesz bases offer a stable and well-conditioned framework ideal for Hilbert spaces, ensuring unique expansions with norm equivalence properties that simplify analysis. Schauder bases provide greater generality, applicable in Banach spaces, but may lack the strong orthogonality and norm preservation features of Riesz bases. Selecting the appropriate basis depends on the specific structure of the function space and the desired balance between stability, convergence, and generality in functional analysis.
Riesz basis Infographic
 libterm.com
libterm.com