A topological space is a fundamental concept in mathematics that generalizes the notion of geometric shapes and spatial properties without relying on specific distances. It consists of a set equipped with a collection of open subsets that satisfy certain axioms, enabling the analysis of continuity, convergence, and boundary properties within various contexts. To explore how topological spaces shape modern mathematical theory and applications, read on.
Table of Comparison
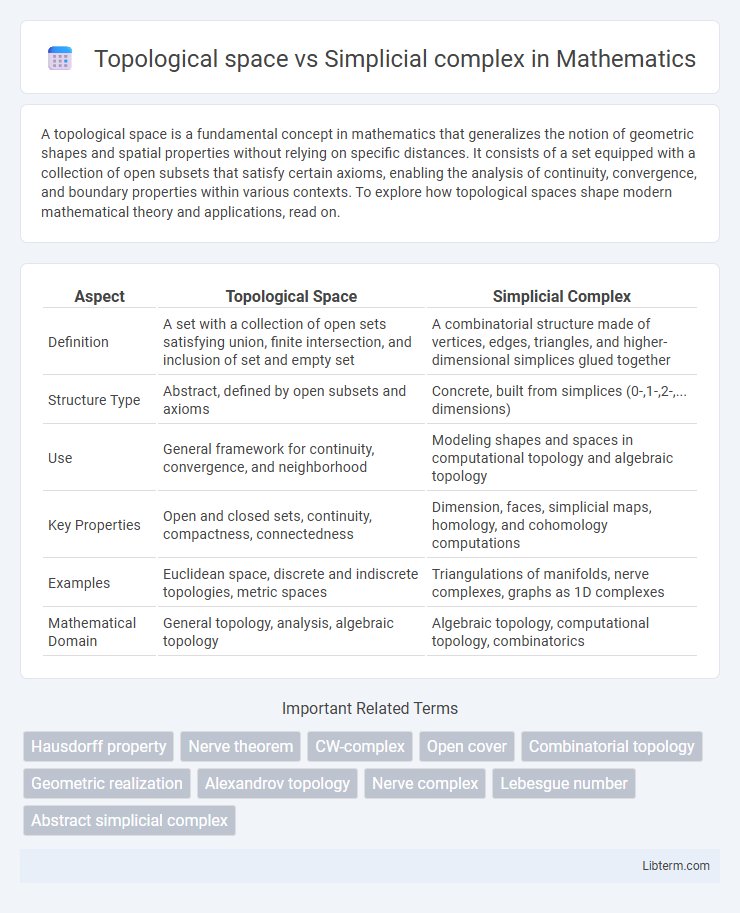
| Aspect | Topological Space | Simplicial Complex |
|---|---|---|
| Definition | A set with a collection of open sets satisfying union, finite intersection, and inclusion of set and empty set | A combinatorial structure made of vertices, edges, triangles, and higher-dimensional simplices glued together |
| Structure Type | Abstract, defined by open subsets and axioms | Concrete, built from simplices (0-,1-,2-,... dimensions) |
| Use | General framework for continuity, convergence, and neighborhood | Modeling shapes and spaces in computational topology and algebraic topology |
| Key Properties | Open and closed sets, continuity, compactness, connectedness | Dimension, faces, simplicial maps, homology, and cohomology computations |
| Examples | Euclidean space, discrete and indiscrete topologies, metric spaces | Triangulations of manifolds, nerve complexes, graphs as 1D complexes |
| Mathematical Domain | General topology, analysis, algebraic topology | Algebraic topology, computational topology, combinatorics |
Introduction to Topological Spaces and Simplicial Complexes
Topological spaces provide a framework for studying continuity and convergence through open sets, defining properties like compactness and connectedness without relying on a specific geometric structure. Simplicial complexes consist of vertices, edges, and higher-dimensional simplices arranged combinatorially to model constructive topological spaces, facilitating computation in algebraic topology. Understanding simplicial complexes aids in discretizing topological spaces, enabling algorithmic analysis of features such as homology and fundamental groups.
Fundamental Definitions
A topological space is a set equipped with a collection of open sets satisfying union, finite intersection, and inclusion of the set itself and the empty set, providing a framework for continuity and convergence. A simplicial complex is a combinatorial structure made up of vertices, edges, triangles, and higher-dimensional simplices glued together along their faces, enabling discrete approximations of topological spaces. The fundamental difference lies in their definitions: topological spaces emphasize open-set axioms and continuity, while simplicial complexes focus on finite collections of simplexes assembled via face relations to model geometric shapes algebraically.
Key Properties and Axioms
Topological spaces are defined by open sets satisfying axioms of union, finite intersection, and inclusion of the entire set and empty set, providing a flexible framework for continuity and convergence. Simplicial complexes consist of vertices, edges, and higher-dimensional simplices arranged to satisfy the closure property that every face of a simplex is also in the complex, enforcing combinatorial and geometric structure. Key distinctions include the reliance on set-theoretic open sets in topological spaces versus the combinatorial assembly of simplices with incidence relations in simplicial complexes.
Examples of Topological Spaces
Topological spaces include familiar examples such as the Euclidean space \(\mathbb{R}^n\), metric spaces like the real line with the standard distance, and the unit circle \(S^1\) with its subspace topology. These spaces are defined by open sets that satisfy axioms of union, intersection, and inclusion of the entire set and empty set, capturing continuity and convergence abstractly. In contrast, a simplicial complex is built from vertices, edges, and higher-dimensional simplices, often serving as a combinatorial model to study topology via discrete building blocks.
Examples of Simplicial Complexes
Simplicial complexes are combinatorial structures consisting of vertices, edges, triangles, and higher-dimensional simplices that fit together in a specific way, providing a discrete model for topological spaces. Examples of simplicial complexes include the boundary of a tetrahedron (a 2-dimensional complex made of four triangular faces), the triangulated surface of a torus constructed from hexagons subdivided into triangles, and the Vietoris-Rips complex generated from a set of points in a metric space, where simplices correspond to clusters of points within a fixed distance. These examples illustrate how simplicial complexes serve as a bridge between abstract topological spaces and computational topology, enabling algebraic analysis via simplices and their incidence relations.
Comparison: Structure and Construction
Topological spaces provide a broad framework defined by open sets to study continuity and convergence, while simplicial complexes are combinatorial structures built from vertices, edges, and higher-dimensional simplices arranged in a specific pattern. The construction of a topological space is abstract, often relying on axioms governing open sets, whereas simplicial complexes have an explicit geometric realization composed of glued simplices that approximate topological spaces. Simplicial complexes enable algorithmic manipulation and computational topology, contrasting the more flexible but less constructive nature of general topological spaces.
Topological Equivalence and Homotopy
Topological spaces provide a broad framework for describing geometric properties preserved under continuous deformations, while simplicial complexes offer a combinatorial structure composed of simplices that facilitate computational topology. Topological equivalence, or homeomorphism, asserts that two spaces can be continuously transformed into each other, capturing their intrinsic geometric similarity, whereas homotopy represents a weaker relation focusing on continuous deformations preserving essential topological features like connectedness and holes. Simplicial complexes serve as discrete models enabling the computation of homotopy groups and homology, crucial for analyzing topological equivalence within topological spaces.
Applications in Mathematics and Science
Topological spaces provide a fundamental framework for studying continuity and convergence in mathematics, crucial for fields like analysis, geometry, and dynamical systems. Simplicial complexes enable combinatorial and computational approaches to topology by decomposing spaces into simple building blocks, extensively used in algebraic topology, mesh generation, and computational geometry. Applications in science include data analysis via persistent homology, where simplicial complexes capture shape features, while topological spaces underpin models in cosmology and material science for understanding spatial properties.
Advantages and Limitations
Topological spaces provide a broad and flexible framework for studying continuity and convergence, accommodating a wide variety of geometric and abstract structures, but they often lack the combinatorial richness needed for algorithmic applications. Simplicial complexes offer a discrete, combinatorial approach to topology that facilitates computational analysis and visualization through their finite simplices, yet they can oversimplify or fail to capture continuous topological nuances present in more general spaces. While topological spaces excel in theoretical generality, simplicial complexes are advantageous for practical computations in areas like algebraic topology and data analysis, though their combinatorial constraints may limit expressiveness.
Summary and Further Reading
Topological spaces provide a general framework for studying concepts of continuity and convergence, characterized by open sets and neighborhood structures, while simplicial complexes offer a combinatorial approach using vertices, edges, and higher-dimensional simplices to model topological spaces discretely. Understanding the interplay between these structures enables deeper insights into algebraic topology and computational topology. For further reading, explore Hatcher's *Algebraic Topology* and Munkres' *Topology* for foundational theories, alongside Edelsbrunner and Harer's *Computational Topology* for applied perspectives on simplicial complexes.
Topological space Infographic
 libterm.com
libterm.com