Large categories and small categories differ based on the size of their collections of objects and morphisms, crucial for foundational aspects of category theory. Abelian categories provide a rich framework for homological algebra by generalizing groups and modules, while monoidal categories introduce tensor products that structure objects with associative operations and identity elements. Explore the rest of this article to deepen your understanding of these concepts and their role in the theory of Topos.
Table of Comparison
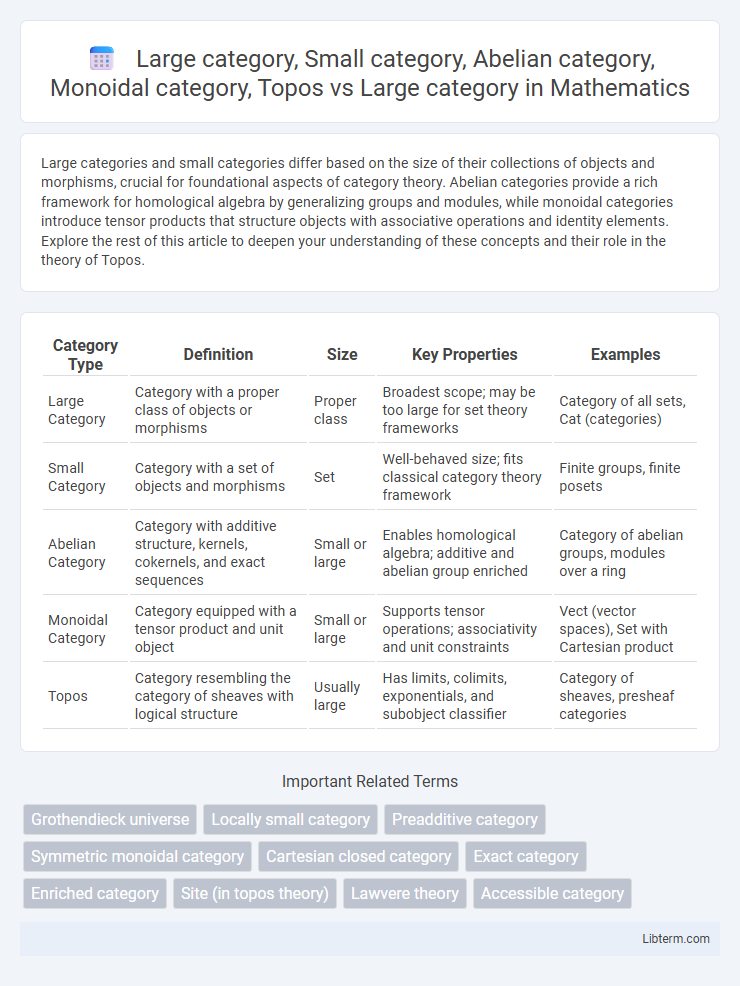
| Category Type | Definition | Size | Key Properties | Examples |
|---|---|---|---|---|
| Large Category | Category with a proper class of objects or morphisms | Proper class | Broadest scope; may be too large for set theory frameworks | Category of all sets, Cat (categories) |
| Small Category | Category with a set of objects and morphisms | Set | Well-behaved size; fits classical category theory framework | Finite groups, finite posets |
| Abelian Category | Category with additive structure, kernels, cokernels, and exact sequences | Small or large | Enables homological algebra; additive and abelian group enriched | Category of abelian groups, modules over a ring |
| Monoidal Category | Category equipped with a tensor product and unit object | Small or large | Supports tensor operations; associativity and unit constraints | Vect (vector spaces), Set with Cartesian product |
| Topos | Category resembling the category of sheaves with logical structure | Usually large | Has limits, colimits, exponentials, and subobject classifier | Category of sheaves, presheaf categories |
Introduction to Category Theory
Large categories extend the concept of small categories by allowing collections of objects and morphisms too vast to form sets, often modeled as proper classes, thereby accommodating more complex mathematical structures. Abelian categories generalize the properties of abelian groups and modules, providing an environment for exact sequences and homological algebra essential in modern algebraic geometry and representation theory. Monoidal categories enrich category theory with a tensor product operation and an identity object, facilitating the study of algebraic structures and topological quantum field theories, while toposes unify geometric and logical concepts, serving as generalized spaces that extend large categories by incorporating internal logic and sheaf-theoretic frameworks.
What is a Large Category?
A Large category is a category whose collection of objects or morphisms forms a proper class rather than a set, distinguishing it from Small categories which have sets of objects and morphisms. Abelian categories are special categories equipped with additive structures and exact sequences, often forming Small categories but can also be Large when dealing with extensive algebraic structures. Monoidal categories introduce tensor products and associativity constraints, while Topos generalizes set theory concepts and can be Large or Small depending on their underlying structure.
Small Category: Definition and Examples
A small category consists of a set of objects and morphisms, where both collections are sets rather than proper classes, enabling concrete constructions and computations. Examples include the category of finite sets, where objects are finite sets and morphisms are functions, and the category of vector spaces over a fixed field with linear maps. Unlike large categories, which may involve proper classes of objects or morphisms, small categories facilitate rigorous treatments in category theory, forming foundational structures in algebra, topology, and theoretical computer science.
Understanding Abelian Categories
Abelian categories generalize the concept of abelian groups to a categorical framework, providing a setting where kernels, cokernels, and exact sequences behave analogously to modules over a ring. Unlike large categories, which can have classes of objects too big to form a set, abelian categories are typically small or locally small, ensuring manageable morphism sets and categorical constructions. Comparing to monoidal categories and toposes, abelian categories specifically emphasize additive structures and exactness properties critical for homological algebra and representation theory.
Exploring Monoidal Categories
Monoidal categories generalize algebraic structures by equipping categories with a tensor product and unit object, facilitating the study of multilinear operations. Unlike large or small categories, which are distinguished by the size of their object classes, monoidal categories emphasize compositional frameworks important in category theory and mathematical physics. Topos theory extends category theory into a context including logical and geometric structures, whereas monoidal categories focus on algebraic coherence, enabling applications in quantum computing, knot theory, and representation theory.
Key Differences: Large vs. Small Categories
Large categories have a class of objects too big to form a set, while small categories have a set of objects and morphisms, making them foundational in category theory. Abelian categories are additive categories with kernels and cokernels, while monoidal categories come with a tensor product and associativity constraints, essential for studying tensor calculus and quantum groups. Topos theory generalizes set theory and logic, forming a category that resembles the category of sets, and unlike large categories, toposes are often Grothendieck toposes that are locally small, highlighting a key distinction in size and logical structure versus large category frameworks.
Structural Properties of Abelian Categories
Abelian categories are characterized by having all morphisms possess kernels and cokernels, ensuring exact sequences which enable a robust structural framework for homological algebra. Unlike large categories that may have proper classes of morphisms, Abelian categories maintain a well-behaved set-theoretic size enabling precise control over morphism composition and factorization. Monoidal categories focus on tensor product structures, while topoi generalize sheaf categories with intrinsic logical frameworks; the structural richness of Abelian categories lies primarily in their additive and exactness properties facilitating homological methods.
Applications of Monoidal Categories
Monoidal categories provide a powerful framework for modeling tensor products and compositional processes in algebra, quantum computing, and theoretical computer science, enabling structured reasoning about resource combination and information flow. Unlike large or small categories, which distinguish size constraints on objects and morphisms, monoidal categories incorporate an additional tensor product operation with associativity and unit constraints, making them essential in the study of braided categories, knot theory, and quantum groups. While Abelian categories focus on exact sequences and homological algebra, and toposes generalize set theory and logic categorically, monoidal categories specifically facilitate applications in quantum protocols, concurrent systems, and categorical semantics of programming languages.
Topos vs. Large Category: Comparative Analysis
Topos and large categories differ fundamentally in structure and scope; a topos is a category with finite limits, exponentials, and a subobject classifier, enabling it to generalize set theory and support internal logic, whereas large categories primarily refer to categories whose collections of objects form proper classes rather than sets. Abelian categories are additive categories with kernels and cokernels making them suitable for homological algebra, while monoidal categories feature tensor products and unit objects facilitating discussions of multiplicative structures. In the comparative analysis of topos versus large category, toposes have rich internal logical frameworks and categorical completeness properties, contrasting with large categories that emphasize size considerations and often lack such internal logical structure.
Conclusion: Interrelationships in Category Theory
Large categories encompass small categories as their subcollections, with abelian categories forming a specialized class characterized by exact sequences and additive structures. Monoidal categories extend these frameworks by introducing tensor products that enable the study of objects with a multiplicative composition, while topoi provide generalized spaces blending geometric and logical features within a categorical context. The interplay among these categories reveals a hierarchical and structural richness in category theory, where large categories host smaller, more structured categories that retain crucial algebraic and logical properties, facilitating unified approaches across mathematics and theoretical computer science.
Large category, Small category, Abelian category, Monoidal category, Topos Infographic
 libterm.com
libterm.com