Harmonic patterns reveal underlying market trends by identifying recurring price movements that traders use to predict potential reversals and continuations. Recognizing these precise geometric shapes based on Fibonacci ratios can enhance Your trading strategy with better entry and exit points. Explore the full article to master harmonic patterns and improve Your market analysis.
Table of Comparison
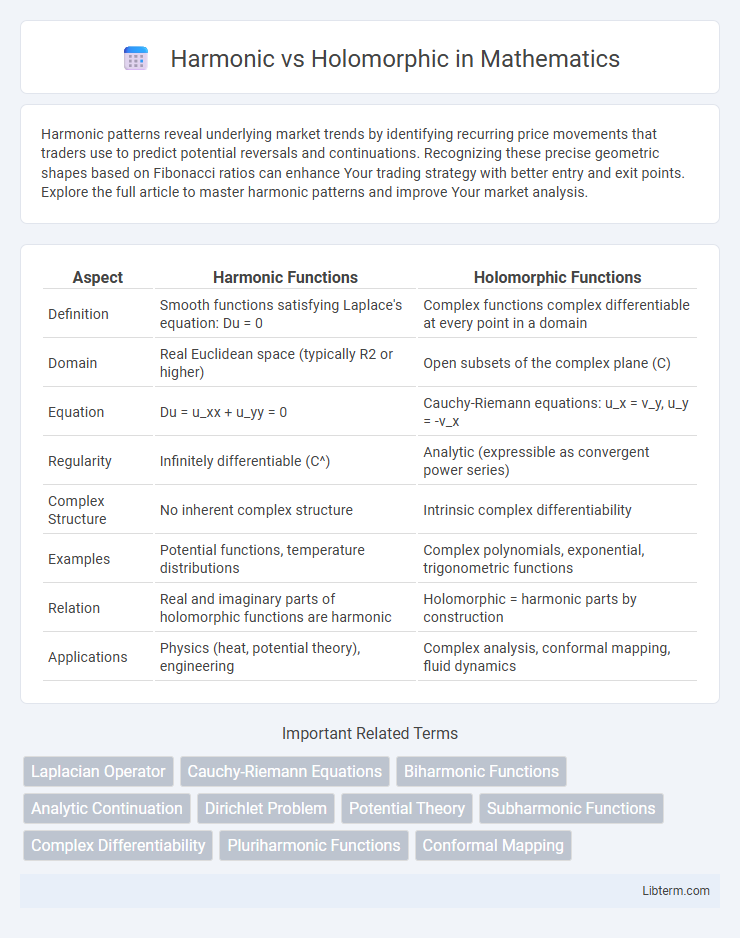
| Aspect | Harmonic Functions | Holomorphic Functions |
|---|---|---|
| Definition | Smooth functions satisfying Laplace's equation: Du = 0 | Complex functions complex differentiable at every point in a domain |
| Domain | Real Euclidean space (typically R2 or higher) | Open subsets of the complex plane (C) |
| Equation | Du = u_xx + u_yy = 0 | Cauchy-Riemann equations: u_x = v_y, u_y = -v_x |
| Regularity | Infinitely differentiable (C^) | Analytic (expressible as convergent power series) |
| Complex Structure | No inherent complex structure | Intrinsic complex differentiability |
| Examples | Potential functions, temperature distributions | Complex polynomials, exponential, trigonometric functions |
| Relation | Real and imaginary parts of holomorphic functions are harmonic | Holomorphic = harmonic parts by construction |
| Applications | Physics (heat, potential theory), engineering | Complex analysis, conformal mapping, fluid dynamics |
Introduction to Harmonic and Holomorphic Functions
Harmonic functions are twice continuously differentiable functions satisfying Laplace's equation, making them essential in potential theory and physics for modeling steady-state heat distribution and gravitational fields. Holomorphic functions, defined as complex functions that are complex-differentiable at every point in their domain, are fundamental in complex analysis due to their strong differentiability properties and connections to analytic functions. The deep relationship between these functions is highlighted by the fact that the real and imaginary parts of holomorphic functions are harmonic, bridging complex analysis and partial differential equations.
Mathematical Definitions: Harmonic vs Holomorphic
Harmonic functions satisfy Laplace's equation, meaning their second partial derivatives sum to zero, ensuring mean value property and smoothness within their domain. Holomorphic functions, defined on complex domains, are complex differentiable and satisfy the Cauchy-Riemann equations, a stricter condition that guarantees analyticity. Every holomorphic function's real and imaginary parts are harmonic, but not all harmonic functions are holomorphic.
Analytical Properties and Differences
Harmonic functions satisfy Laplace's equation and are infinitely differentiable, exhibiting mean value properties and non-oscillatory behavior, while holomorphic functions are complex differentiable and conformal, preserving angles locally. Holomorphic functions inherently possess harmonic real and imaginary parts due to the Cauchy-Riemann equations, establishing a direct analytical link between the two. Unlike harmonic functions, holomorphic functions are analytic and fully determined by their values on any small neighborhood, reflecting stronger constraints and richer structure in complex analysis.
Geometric Interpretations
Harmonic functions represent scalar fields where the Laplace equation holds, describing steady-state heat distribution or gravitational potential, and their level sets form equipotential curves with no local maxima or minima inside the domain. Holomorphic functions, complex-differentiable in a neighborhood, encode conformal mappings preserving angles and local shapes, leading to geometric interpretations involving complex analytic curves and natural generalizations of harmonic functions as their real and imaginary parts solve Laplace's equation. The interplay between harmonic and holomorphic functions underpins geometric function theory, linking potential theory with conformal geometry through the Cauchy-Riemann equations.
Roles in Complex Analysis
Harmonic functions, characterized by satisfying Laplace's equation, play a crucial role in potential theory and serve as real-valued solutions governing physical phenomena like heat and fluid flow. Holomorphic functions, defined as complex functions differentiable everywhere in a domain, form the foundation of complex analysis due to their strong analytic properties and ability to generate harmonic functions through their real and imaginary parts. The interplay between harmonic and holomorphic functions enables solving boundary value problems and understanding conformal mappings within the complex plane.
Physical and Engineering Applications
Harmonic functions, defined by the Laplace equation, model steady-state heat distribution, electrostatics, and incompressible fluid flow in engineering. Holomorphic functions, characterized by complex differentiability, enable conformal mapping techniques essential for solving two-dimensional potential flow and electromagnetic field problems. Both function types provide foundational tools for optimizing design and analysis in physical systems through their unique mathematical properties.
Key Theorems Involving Harmonic and Holomorphic Functions
Harmonic functions satisfy Laplace's equation and are characterized by the mean value property and maximum principle, while holomorphic functions are complex differentiable functions that satisfy the Cauchy-Riemann equations. Key theorems such as the Cauchy Integral Theorem and Morera's Theorem establish that holomorphic functions are infinitely differentiable and conform to integral constraints, linking them closely to harmonic functions, which are their real or imaginary parts. The Dirichlet problem and Poisson's formula demonstrate methods to reconstruct harmonic functions from boundary values, showcasing fundamental connections in potential theory and complex analysis.
Relationship Between Harmonic and Holomorphic Functions
Harmonic functions are twice continuously differentiable functions satisfying Laplace's equation, while holomorphic functions are complex functions that are differentiable in the complex sense. Every holomorphic function's real and imaginary parts are harmonic functions, reflecting a fundamental relationship where holomorphicity implies harmonicity of component functions. This connection enables the use of complex analysis techniques to solve problems involving harmonic functions in fields like potential theory and fluid dynamics.
Examples and Visualizations
Harmonic functions like u(x, y) = x2 - y2 exhibit smooth contours representing solutions to Laplace's equation, while holomorphic functions such as f(z) = z2 = (x + iy)2 combine real and imaginary parts to satisfy the Cauchy-Riemann equations. Visualizing harmonic functions often involves contour plots highlighting equipotential lines, whereas holomorphic functions are depicted using color mappings of their complex values or domain coloring techniques. For instance, the harmonic function Re(z2) matches the real part of the holomorphic function z2, illustrating the deep connection between these classes through explicit examples and graphical interpretations.
Summary and Conclusion
Harmonic functions are real-valued solutions to Laplace's equation characterized by mean value properties and arise in physical phenomena like heat distribution. Holomorphic functions are complex-differentiable functions defined on complex domains, exhibiting strong analytic properties such as conformality and power series representation. The key distinction lies in holomorphic functions being inherently complex with complex derivatives, while harmonic functions are real-valued and often appear as real or imaginary parts of holomorphic functions.
Harmonic Infographic
 libterm.com
libterm.com