Topos refers to common themes or motifs that recur across literature, art, and rhetoric, shaping how stories and arguments are constructed. Understanding topos helps you recognize patterns and conventions that enhance the depth and relatability of creative or persuasive works. Explore the rest of the article to discover how topos can enrich your interpretation and communication skills.
Table of Comparison
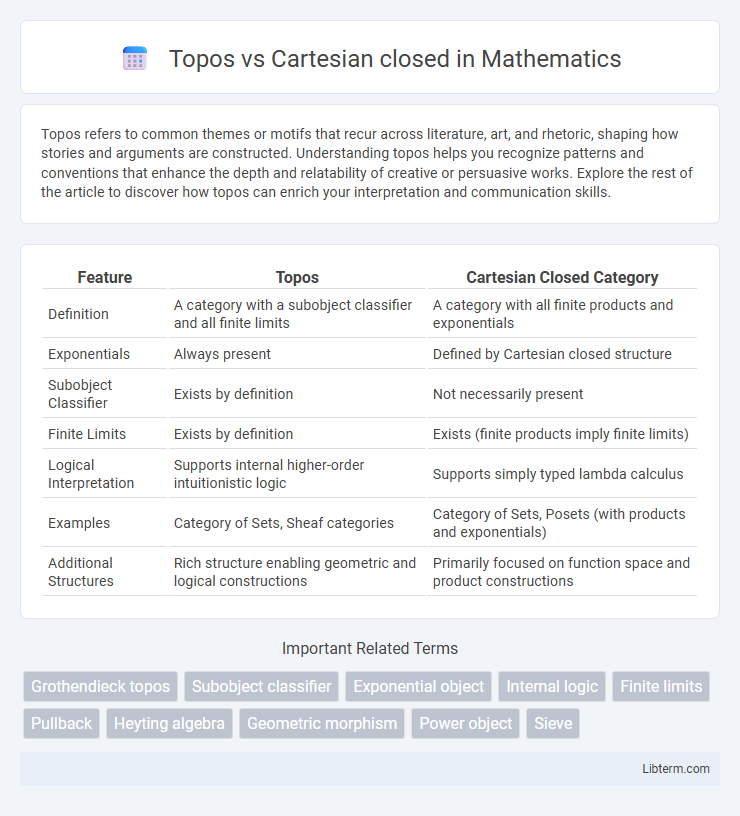
| Feature | Topos | Cartesian Closed Category |
|---|---|---|
| Definition | A category with a subobject classifier and all finite limits | A category with all finite products and exponentials |
| Exponentials | Always present | Defined by Cartesian closed structure |
| Subobject Classifier | Exists by definition | Not necessarily present |
| Finite Limits | Exists by definition | Exists (finite products imply finite limits) |
| Logical Interpretation | Supports internal higher-order intuitionistic logic | Supports simply typed lambda calculus |
| Examples | Category of Sets, Sheaf categories | Category of Sets, Posets (with products and exponentials) |
| Additional Structures | Rich structure enabling geometric and logical constructions | Primarily focused on function space and product constructions |
Introduction to Topos and Cartesian Closed Categories
Topos theory generalizes set theory by modeling categories with internal logic, supporting notions like subobject classifiers and exponential objects. Cartesian closed categories (CCCs) provide a foundational framework where every product has an exponential object, enabling the interpretation of simply typed lambda calculus. The distinction lies in Topos encompassing additional structure such as a subobject classifier, making it a richer framework than CCCs for categorical logic and geometry.
Defining Topos: Key Concepts and Properties
A topos is a category that generalizes the notion of set theory by possessing all finite limits, exponentials, and a subobject classifier, enabling a rich internal logic analogous to higher-order intuitionistic logic. Unlike Cartesian closed categories, which guarantee finite products and exponentials, topoi also ensure the existence of a subobject classifier that classifies monomorphisms, representing a key property distinguishing them. These features make topoi a foundational framework for categorical logic and provide a general setting for sheaf theory, connecting geometry and logic in a unified structure.
Understanding Cartesian Closed Categories
Cartesian closed categories (CCCs) are fundamental structures in category theory characterized by the existence of finite products, an internal hom-functor, and an exponential object for every pair of objects. Unlike general topoi, which are richer categorical structures supporting logical operations and sheaf semantics, CCCs specifically capture the essence of function spaces and lambda calculus models through closedness under exponentiation. Understanding CCCs is crucial for applications in theoretical computer science, particularly in the semantics of typed lambda calculi and functional programming languages.
Core Differences Between Topos and Cartesian Closed Categories
Topos categories generalize set theory with internal logic and include features like subobject classifiers and power objects, enabling a rich internal language that Cartesian closed categories lack. Cartesian closed categories primarily emphasize the existence of exponentials and finite products, supporting function spaces but do not guarantee the presence of a subobject classifier or the full logical structure of a topos. The core difference lies in the topos's capability to model higher-order logic internally, whereas Cartesian closed categories provide only the foundations for lambda calculus and function abstraction without intrinsic logical completeness.
Essential Examples of Topos
Topos theory generalizes set theory by providing a categorical framework that supports logical operations and internal reasoning, with Cartesian closed categories (CCCs) serving as fundamental examples where function spaces exist and exponentiation is well-defined. Essential examples of topoi include the category of sets (Set), the category of sheaves on a topological space, and presheaf categories, each demonstrating the topos axioms such as the existence of limits, colimits, a subobject classifier, and exponentials. Cartesian closed categories are integral to topos theory as every topos is a CCC with additional structure, ensuring internal hom-objects and enabling a rich interpretation of intuitionistic higher-order logic.
Notable Examples of Cartesian Closed Categories
Notable examples of Cartesian closed categories include the category of sets (Set), where the exponential object corresponds to the set of functions between two sets, and the category of finite sets (FinSet), which also supports Cartesian closure. Another important example is the category of presheaves on a small category, which forms a topos and thus is Cartesian closed, illustrating the deep connection between topoi and Cartesian closed categories. These examples highlight how Cartesian closure facilitates function space constructions integral to categorical logic and type theory.
Logical Interpretations in Topos and Cartesian Closed Categories
Topos theory extends Cartesian closed categories by incorporating internal logic through a subobject classifier, enabling the interpretation of higher-order intuitionistic logic within its structure. Cartesian closed categories provide a foundation for simply typed lambda calculus, allowing functional abstraction and application, but lack the intrinsic logical framework furnished by a topos. Logical interpretations in topoi support rich type theories and predicate logic, while Cartesian closed categories primarily model functional programming languages and typed lambda calculi without explicit internal logic or quantification.
Subobject Classifier: Topos vs Cartesian Closed
A topos is characterized by the presence of a subobject classifier, which provides a categorical analogue of the characteristic function for subsets, allowing for a rich internal logic and the interpretation of predicates. In contrast, a Cartesian closed category lacks a subobject classifier, limiting its ability to internally represent truth values and hence to model higher-order logic fully. The existence of a subobject classifier in a topos enables the construction of power objects and supports intuitionistic type theories that a mere Cartesian closed category cannot intrinsically accommodate.
Applications in Mathematics and Computer Science
Topoi provide a generalized framework for categorical logic and enable the interpretation of higher-order type theories, crucial for advancements in algebraic geometry and homotopy theory. Cartesian closed categories (CCCs) underpin the semantics of simply typed lambda calculus, facilitating functional programming language design and type theory implementations. Both structures support the formalization of computational effects and domain theory, enhancing the development of proof assistants and denotational semantics in computer science.
Conclusion: Choosing Between Topos and Cartesian Closed Categories
Choosing between topos and Cartesian closed categories depends on the requirements of the categorical framework and the level of logical structure needed. Toposes provide a richer internal language supporting higher-order logic, subobject classifiers, and exponential objects, making them suitable for models of set theory and sheaf theory. Cartesian closed categories, while simpler, focus on function space structures and are ideal for modeling simply typed lambda calculus and core computational processes.
Topos Infographic
 libterm.com
libterm.com