A surjective function, also known as an onto function, maps every element of its codomain to at least one element of its domain, ensuring complete coverage of the output set. This concept is fundamental in mathematics, especially in fields like algebra and calculus, as it guarantees that every possible output is reached by the function. Explore the rest of the article to deepen your understanding of surjective functions and their applications.
Table of Comparison
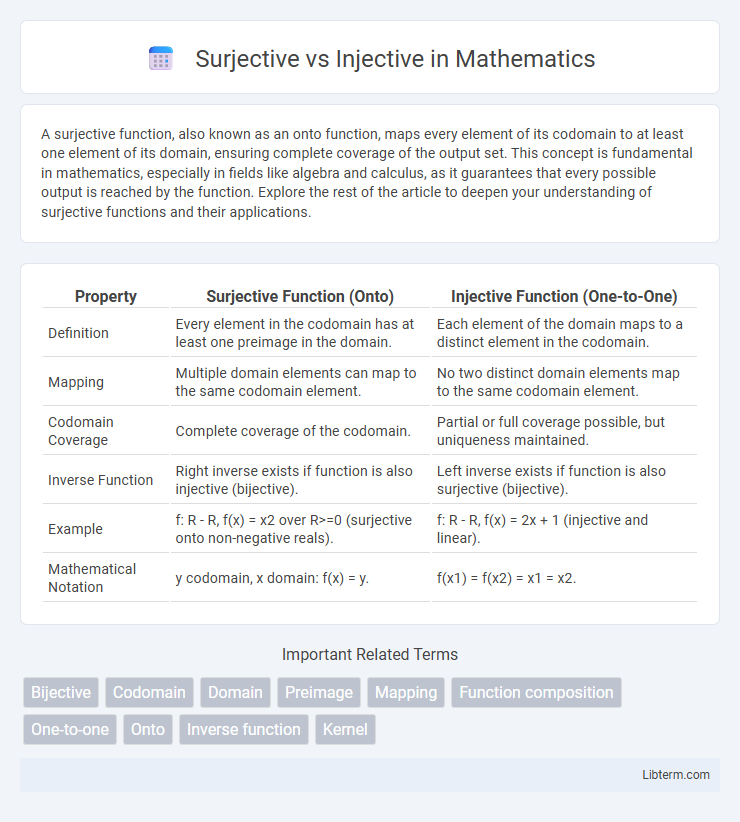
| Property | Surjective Function (Onto) | Injective Function (One-to-One) |
|---|---|---|
| Definition | Every element in the codomain has at least one preimage in the domain. | Each element of the domain maps to a distinct element in the codomain. |
| Mapping | Multiple domain elements can map to the same codomain element. | No two distinct domain elements map to the same codomain element. |
| Codomain Coverage | Complete coverage of the codomain. | Partial or full coverage possible, but uniqueness maintained. |
| Inverse Function | Right inverse exists if function is also injective (bijective). | Left inverse exists if function is also surjective (bijective). |
| Example | f: R - R, f(x) = x2 over R>=0 (surjective onto non-negative reals). | f: R - R, f(x) = 2x + 1 (injective and linear). |
| Mathematical Notation | y codomain, x domain: f(x) = y. | f(x1) = f(x2) = x1 = x2. |
Introduction to Surjective and Injective Functions
Surjective functions, also known as onto functions, map every element in the codomain to at least one element in the domain, ensuring the entire codomain is covered. Injective functions, or one-to-one functions, assign distinct elements in the domain to distinct elements in the codomain, preventing any two domain elements from sharing the same image. Understanding these fundamental concepts is essential in fields like set theory, algebra, and computer science for analyzing function behavior and structure.
Definitions: Surjective, Injective, and Bijective
A surjective function, or onto function, maps every element of the codomain to at least one element in the domain, ensuring the range equals the codomain. An injective function, or one-to-one function, assigns distinct domain elements to distinct codomain elements, preventing any overlap in output values. A bijective function is both injective and surjective, establishing a perfect one-to-one correspondence between the domain and codomain, enabling the existence of an inverse function.
Visualizing Function Types
Visualizing function types enhances understanding of surjective and injective mappings by illustrating their unique characteristics. Injective functions map each element of the domain to a distinct element in the codomain, ensuring no overlaps, often visualized as arrows pointing to separate targets. Surjective functions cover every element of the codomain at least once, demonstrated by arrows collectively hitting all points in the codomain, emphasizing complete coverage.
Mathematical Notation and Symbols
A surjective function \( f: A \to B \) satisfies \( \forall b \in B, \exists a \in A \text{ such that } f(a) = b \), indicating every element in the codomain \( B \) has a preimage in the domain \( A \). An injective function \( f: A \to B \) is defined by \( \forall a_1, a_2 \in A, f(a_1) = f(a_2) \implies a_1 = a_2 \), ensuring distinct inputs map to distinct outputs. The symbolic contrast between surjection and injection highlights coverage of the codomain versus uniqueness of mapping in the domain.
Key Differences Between Surjective and Injective
Surjective functions map every element of the codomain to at least one element of the domain, ensuring full coverage, while injective functions map distinct elements of the domain to distinct elements of the codomain, maintaining uniqueness. A surjective function is also called onto, guaranteeing that every possible output is achieved, whereas an injective function is one-to-one, preventing any overlap in mapped values. The key difference lies in surjectivity emphasizing coverage of the codomain, and injectivity emphasizing the uniqueness of mapping from the domain.
Real-world Examples of Surjective Functions
Surjective functions map every element in the codomain to at least one element in the domain, exemplified by the Celsius-to-Fahrenheit temperature conversion function where every Fahrenheit value corresponds to a Celsius temperature. Another real-world example is the function assigning each student in a class to their grade level, ensuring every grade level has at least one student. These surjective mappings guarantee full coverage of output values, making them essential in modeling scenarios where all outcomes must be represented.
Real-world Examples of Injective Functions
Injective functions assign distinct outputs to each input, ensuring no two inputs share the same output, similar to how each employee ID number uniquely identifies one worker in a company database. In biometric systems, fingerprint recognition serves as an injective function since each fingerprint corresponds to one individual, preventing identity overlaps. Another example is the ISBN system for books, where every ISBN uniquely identifies a single book edition, exemplifying an injective mapping in publishing.
Importance in Mathematical Proofs
Surjective and injective functions play crucial roles in mathematical proofs by ensuring the precise mapping between elements of sets, which is fundamental for establishing bijections and inverses. Surjectivity guarantees every element in the codomain has a preimage, enabling the demonstration of completeness or coverage in mappings. Injectivity ensures uniqueness in mappings, preventing ambiguity and supporting arguments in proofs involving one-to-one correspondence and function invertibility.
Common Misconceptions and Pitfalls
Surjective functions, or onto functions, map every element of the codomain to at least one element of the domain, while injective functions, or one-to-one functions, assign distinct elements of the domain to distinct elements of the codomain. A common misconception is that a function can be both injective and surjective without considering the set sizes; injectivity requires no element in the codomain is mapped by more than one domain element, and surjectivity demands coverage of the entire codomain. Pitfalls include confusing surjectivity with the range being equal to the domain, and overlooking that an injective function may not cover all codomain elements, thus not being surjective.
Summary and Key Takeaways
Surjective functions map every element in the codomain to at least one element in the domain, ensuring full coverage of the target set, while injective functions map distinct elements of the domain to distinct elements of the codomain, highlighting uniqueness. The key takeaway is that surjectivity guarantees every output is attained, whereas injectivity guarantees no two inputs share the same output. Understanding these concepts is essential for exploring function properties in fields like mathematics, computer science, and data analysis.
Surjective Infographic
 libterm.com
libterm.com