A metric is a standard of measurement used to quantify performance, progress, or quality across various fields such as business, technology, and education. Understanding the right metrics ensures effective decision-making and helps track your goals with precision. Explore the rest of the article to learn how to select and apply the most impactful metrics for your needs.
Table of Comparison
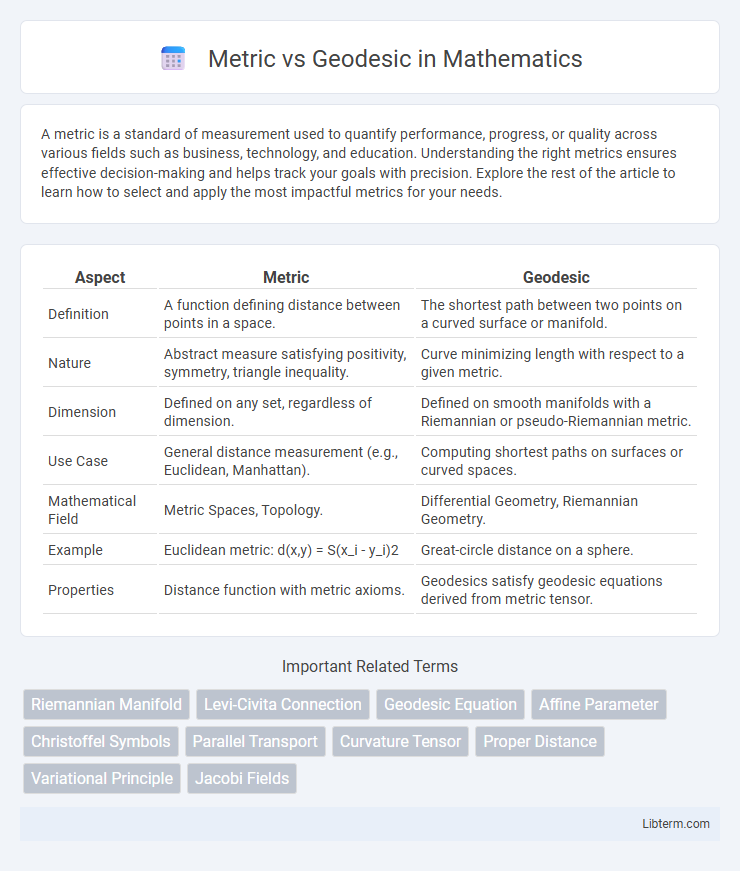
| Aspect | Metric | Geodesic |
|---|---|---|
| Definition | A function defining distance between points in a space. | The shortest path between two points on a curved surface or manifold. |
| Nature | Abstract measure satisfying positivity, symmetry, triangle inequality. | Curve minimizing length with respect to a given metric. |
| Dimension | Defined on any set, regardless of dimension. | Defined on smooth manifolds with a Riemannian or pseudo-Riemannian metric. |
| Use Case | General distance measurement (e.g., Euclidean, Manhattan). | Computing shortest paths on surfaces or curved spaces. |
| Mathematical Field | Metric Spaces, Topology. | Differential Geometry, Riemannian Geometry. |
| Example | Euclidean metric: d(x,y) = S(x_i - y_i)2 | Great-circle distance on a sphere. |
| Properties | Distance function with metric axioms. | Geodesics satisfy geodesic equations derived from metric tensor. |
Introduction to Metric and Geodesic
A metric defines a way to measure distances between points in a given space, facilitating the calculation of geometrical properties such as length and angle. Geodesics represent the shortest paths or curves between two points within that metric space, generalizing the concept of straight lines in Euclidean geometry. Understanding the relationship between metrics and geodesics is fundamental in differential geometry, manifold theory, and applications like general relativity and computer vision.
Defining Metric: Foundations and Importance
Defining a metric involves establishing a function that quantifies the distance between elements in a set, adhering to properties like non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. Metrics form the foundational framework in topology and analysis, enabling the formalization of concepts such as convergence, continuity, and compactness within metric spaces. The importance of metrics lies in their ability to generalize intuitive geometric notions of distance to abstract spaces, facilitating rigorous study across mathematics, physics, and computer science.
Understanding Geodesics: The Shortest Path Concept
Geodesics represent the shortest path between two points on a curved surface, defined by the intrinsic geometry of the space rather than Euclidean distance. Metrics provide the means to measure distances and angles locally, enabling the precise calculation of geodesics through differential equations in Riemannian geometry. Understanding geodesics is crucial in fields like general relativity and navigation, where shortest path concepts govern particle trajectories and route optimization on curved manifolds.
Mathematical Formulation of Metrics
The mathematical formulation of metrics involves defining a metric tensor \( g_{ij} \) on a manifold, which assigns an inner product to tangent vectors, enabling the calculation of distances and angles. Geodesics are curves that locally minimize the length functional derived from the metric, characterized by the geodesic equation \( \frac{d^2 x^k}{dt^2} + \Gamma^k_{ij} \frac{dx^i}{dt} \frac{dx^j}{dt} = 0 \), where \( \Gamma^k_{ij} \) are the Christoffel symbols computed from the metric tensor. The metric's positive-definiteness ensures well-defined distances, while geodesics represent solutions to the variational problem of minimizing the integral of the metric-induced arc length.
Geodesics in Riemannian Geometry
Geodesics in Riemannian geometry are curves that locally minimize distance with respect to the Riemannian metric, representing the shortest paths between points on a curved manifold. Unlike general metric spaces where distance is abstract, geodesics are defined by solving the geodesic equation derived from the Levi-Civita connection associated with the metric tensor. These curves play a crucial role in understanding the intrinsic geometry of manifolds, including applications in general relativity and differential geometry analysis.
Key Differences Between Metric and Geodesic
A metric defines a distance function quantifying the shortest path between two points in a space, while a geodesic represents the actual curve or path that realizes this shortest distance under the given metric. Metrics provide the mathematical framework to measure lengths, whereas geodesics are the solutions to variational problems minimizing these lengths, often characterized by differential equations. Key differences include that a metric is a function assigning distances, and geodesics are geometric objects dependent on that metric, reflecting intrinsic curvature and space topology.
Metric Spaces vs. Geodesic Spaces
Metric spaces define distances between points through a distance function satisfying non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, allowing analysis of abstract geometric structures. Geodesic spaces are a special class of metric spaces where every pair of points is connected by a shortest path or geodesic, ensuring the existence of curves minimizing distance. The distinction is crucial in topology and geometry, with geodesic spaces enabling more precise studies of curvature and shape compared to general metric spaces.
Applications of Metrics in Physics and Mathematics
Metrics serve as fundamental tools in both physics and mathematics by quantifying the distance between points in various spaces, enabling precise analysis of geometrical and topological properties. In general relativity, the metric tensor defines the curvature of spacetime, governing gravitational interactions and light propagation. In mathematics, metrics facilitate the study of metric spaces, enabling convergence, continuity, and compactness analyses vital for functional analysis and topology.
Real-World Uses of Geodesics
Geodesics represent the shortest paths on curved surfaces and are fundamental in GPS technology for accurately calculating distances on Earth's spheroidal shape. In aerospace navigation, geodesic computations optimize flight routes by accounting for Earth's curvature, reducing fuel consumption and travel time. Geodesic principles also underpin the design of geodesic domes, combining structural strength with material efficiency in architecture and engineering.
Summary: Choosing Between Metric and Geodesic
Selecting between metric and geodesic depends on the context and desired precision in spatial analysis. Metrics provide straightforward distance calculations based on coordinate systems, making them suitable for simple, flat-plane measurements. Geodesics account for the Earth's curvature, offering more accurate distance and path calculations over global scales, essential for navigation and geospatial applications.
Metric Infographic
 libterm.com
libterm.com