Submodular functions are set functions that exhibit a natural diminishing returns property, meaning the incremental gain from adding an element to a set decreases as the set grows larger. This property makes them highly valuable in fields such as machine learning, economics, and combinatorial optimization for solving problems related to coverage, diversity, and feature selection. Explore the rest of the article to understand how leveraging submodular functions can optimize your decision-making processes.
Table of Comparison
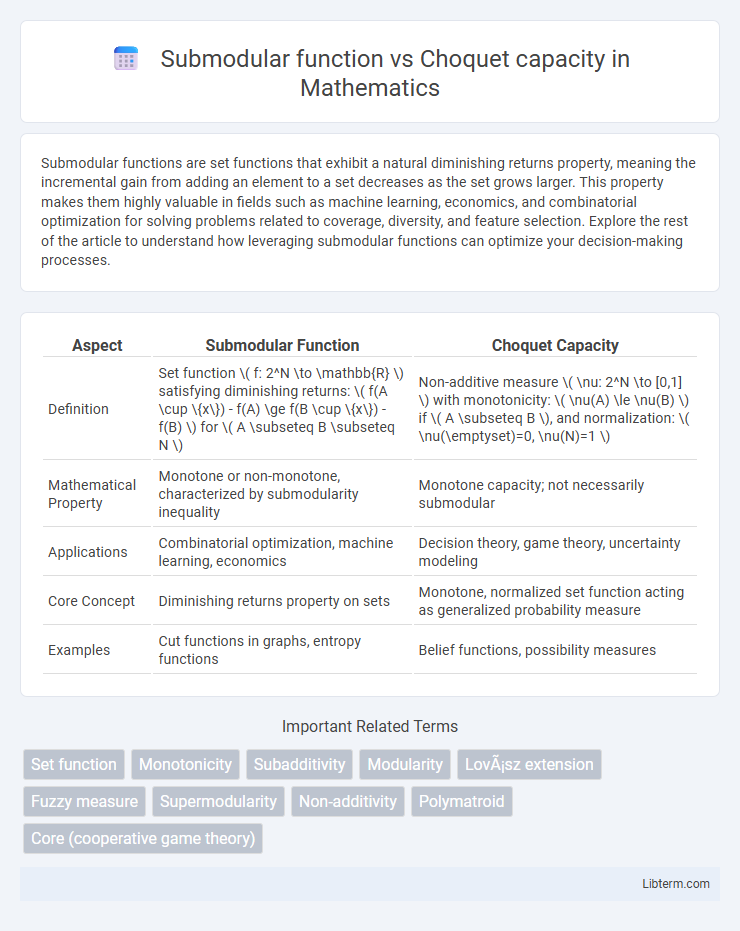
| Aspect | Submodular Function | Choquet Capacity |
|---|---|---|
| Definition | Set function \( f: 2^N \to \mathbb{R} \) satisfying diminishing returns: \( f(A \cup \{x\}) - f(A) \ge f(B \cup \{x\}) - f(B) \) for \( A \subseteq B \subseteq N \) | Non-additive measure \( \nu: 2^N \to [0,1] \) with monotonicity: \( \nu(A) \le \nu(B) \) if \( A \subseteq B \), and normalization: \( \nu(\emptyset)=0, \nu(N)=1 \) |
| Mathematical Property | Monotone or non-monotone, characterized by submodularity inequality | Monotone capacity; not necessarily submodular |
| Applications | Combinatorial optimization, machine learning, economics | Decision theory, game theory, uncertainty modeling |
| Core Concept | Diminishing returns property on sets | Monotone, normalized set function acting as generalized probability measure |
| Examples | Cut functions in graphs, entropy functions | Belief functions, possibility measures |
Introduction to Submodular Functions and Choquet Capacities
Submodular functions are set functions characterized by the property of diminishing returns, meaning that the incremental gain from adding an element to a set decreases as the set grows. Choquet capacities generalize probability measures by assigning non-additive set functions that capture interaction among elements, allowing for modeling uncertainty without requiring additivity. Both concepts underpin optimization and decision-making, with submodular functions enabling efficient algorithms for combinatorial problems, while Choquet capacities provide a framework for risk assessment and aggregation under ambiguity.
Mathematical Definition of Submodular Functions
A submodular function is a set function \( f: 2^N \to \mathbb{R} \) defined on the power set of a finite set \( N \), satisfying the diminishing returns property: for all subsets \( A \subseteq B \subseteq N \) and elements \( x \in N \setminus B \), it holds that \( f(A \cup \{x\}) - f(A) \geq f(B \cup \{x\}) - f(B) \). Formally, \( f \) is submodular if for every pair of subsets \( S, T \subseteq N \), the inequality \( f(S) + f(T) \geq f(S \cup T) + f(S \cap T) \) is satisfied, indicating a form of concavity over sets. In contrast, a Choquet capacity is a monotone set function \( \nu: 2^N \to [0,1] \) that is normalized with \( \nu(\emptyset) = 0 \) and \( \nu(N) = 1 \), generally lacking the diminishing returns property characteristic of submodular functions.
Formal Definition of Choquet Capacity
A Choquet capacity is defined as a set function \(\nu: 2^X \to [0,1]\) on a finite set \(X\) that is monotone, meaning \(\nu(A) \leq \nu(B)\) whenever \(A \subseteq B \subseteq X\), with \(\nu(\emptyset) = 0\) and \(\nu(X) = 1\). In contrast to submodular functions, which satisfy the diminishing returns property \(\nu(A \cup \{x\}) - \nu(A) \geq \nu(B \cup \{x\}) - \nu(B)\) for \(A \subseteq B\), Choquet capacities only require monotonicity without necessarily fulfilling submodularity. The Choquet capacity serves as the foundational concept for defining non-additive measures in decision theory and fuzzy measures, differing structurally from submodular functions despite some overlapping properties.
Key Properties of Submodular Functions
Submodular functions exhibit the diminishing returns property, meaning the incremental gain from adding an element to a set decreases as the set grows, which is critical in optimization and machine learning. These functions are monotone or non-monotone, possess polynomial-time minimization algorithms, and can be characterized by their Lovasz extension, enabling continuous optimization techniques. In contrast, Choquet capacities generalize measure theory without necessarily exhibiting submodularity but share notions of non-additivity and monotonicity, thus serving different applications in decision theory and game theory.
Fundamental Properties of Choquet Capacities
Choquet capacities are set functions characterized by monotonicity and normalization, ensuring that the capacity of the empty set is zero and the entire space is assigned a capacity of one, which establishes a foundation for integration theories like the Choquet integral. Unlike submodular functions that satisfy diminishing returns properties through a submodularity inequality, Choquet capacities primarily rely on monotone set functions without the necessity of submodularity, allowing for representation of non-additive measures. The fundamental properties of Choquet capacities include monotonicity, continuity from below for increasing sequences of sets, and the ability to capture uncertainty and aggregation beyond additive probabilities, distinguishing them from submodular functions in both theoretical formulation and practical applications.
Differences in Set Function Representation
Submodular functions are characterized by diminishing returns and satisfy the property f(A) + f(B) >= f(A B) + f(A B) for sets A and B, enabling efficient optimization in combinatorial settings. Choquet capacities, defined as monotone set functions with normalized values (0 for the empty set and 1 for the full set), generalize measures by allowing non-additive behavior with respect to union of sets. The key difference in set function representation lies in submodular functions emphasizing diminishing returns and balance between intersections and unions, whereas Choquet capacities focus on monotonicity and normalization without requiring submodularity.
Optimization Applications: Submodular Functions vs. Choquet Capacities
Submodular functions, characterized by diminishing returns properties, are widely utilized in combinatorial optimization for tasks like sensor placement, influence maximization, and document summarization due to their tractable optimization via greedy algorithms. Choquet capacities, representing non-additive set functions tied to fuzzy measures, offer flexibility in modeling interactions and uncertainty, often applied in multi-criteria decision-making and game theory but with more complex optimization landscapes. Optimization involving submodular functions benefits from efficient approximation guarantees, while Choquet capacities require advanced methods, such as non-linear programming or heuristic approaches, to handle the non-modular and potentially non-submodular structures inherent in capacity-based models.
Connections in Decision Theory and Economics
Submodular functions and Choquet capacities both capture notions of diminishing returns and non-additive measures, essential in modeling preferences and uncertainty in decision theory and economics. Submodular functions characterize economically relevant properties like decreasing marginal utility, while Choquet capacities generalize probability measures to represent ambiguity and non-linear expectations. These frameworks intersect in representing decision-makers' behavior under uncertainty and ambiguity, facilitating more accurate models of risk aversion, belief functions, and cooperative game theory.
Comparative Examples and Use Cases
Submodular functions, such as coverage functions in sensor placement, characterize diminishing returns and find wide applications in machine learning for feature selection, whereas Choquet capacities model non-additive set functions used in decision theory to capture interaction effects among criteria. For example, submodular functions efficiently optimize influence maximization in social networks by selecting the most impactful nodes, while Choquet capacities enable aggregation of expert opinions with varying degrees of importance and synergy. Use cases highlight submodular functions' scalability in combinatorial optimization and Choquet capacities' flexibility in representing fuzzy measures and uncertainty in multicriteria decision-making models.
Conclusion: Choosing Between Submodular Functions and Choquet Capacities
Submodular functions offer efficient optimization techniques and clear combinatorial interpretations, making them ideal for tasks involving information gain and coverage problems. Choquet capacities provide greater flexibility in modeling interactions and dependencies, particularly in decision-making scenarios with uncertainty and non-additive measures. Selecting between them hinges on balancing computational tractability with the need for intricate dependency modeling in a given application.
Submodular function Infographic
 libterm.com
libterm.com