Identity shapes your understanding of self and influences how you interact with the world around you. Exploring personal identity involves examining cultural, social, and psychological factors that define who you are. Discover more about the complexities of identity and how it impacts your life in the rest of this article.
Table of Comparison
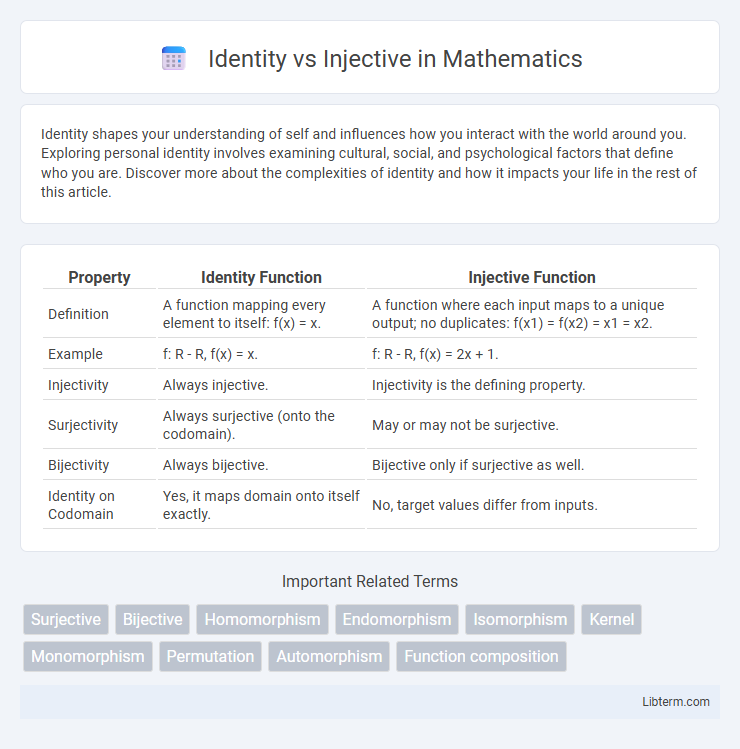
| Property | Identity Function | Injective Function |
|---|---|---|
| Definition | A function mapping every element to itself: f(x) = x. | A function where each input maps to a unique output; no duplicates: f(x1) = f(x2) = x1 = x2. |
| Example | f: R - R, f(x) = x. | f: R - R, f(x) = 2x + 1. |
| Injectivity | Always injective. | Injectivity is the defining property. |
| Surjectivity | Always surjective (onto the codomain). | May or may not be surjective. |
| Bijectivity | Always bijective. | Bijective only if surjective as well. |
| Identity on Codomain | Yes, it maps domain onto itself exactly. | No, target values differ from inputs. |
Understanding Identity in Mathematics
Identity in mathematics refers to a function that maps every element to itself, ensuring f(x) = x for all x in the domain. This concept is crucial for distinguishing identity functions from injective functions, which require that distinct inputs map to distinct outputs, but do not necessarily map each element to itself. Understanding identity functions helps clarify foundational ideas in set theory and function analysis, emphasizing the preservation of elements without alteration.
Defining Injective (One-to-One) Functions
An injective function, also known as a one-to-one function, maps each element of the domain to a unique element in the codomain, ensuring no two different inputs produce the same output. This property guarantees distinctness, meaning if f(x1) = f(x2), then x1 must equal x2, preventing any value from being duplicated in the range. Injective functions are fundamental in mathematics for establishing one-to-one correspondences and are critical in areas such as set theory, combinatorics, and function inversion.
Key Differences: Identity vs Injective
Identity functions map every element to itself, preserving the original input without any change. Injective functions, also known as one-to-one functions, assign unique outputs to distinct inputs, ensuring no two different inputs share the same output. The key difference lies in identity functions being a specific case of injective functions where the output equals the input, while injective functions guarantee uniqueness without necessarily preserving the original input.
Visualizing Identity and Injective Mappings
Visualizing identity mappings involves observing a function where every element maps directly to itself, represented graphically by points lying on the line y = x in a coordinate plane. In contrast, injective mappings ensure that distinct elements from the domain map to distinct elements in the codomain, creating a one-to-one relationship that can be visualized by a function graph that never touches the same horizontal line twice. Understanding these visual distinctions helps clarify the fundamental concept that identity functions are a specific case of injective functions with perfect self-correspondence at every point.
Mathematical Properties of Identity Functions
Identity functions, defined as f(x) = x for all elements in a set, exhibit both injective (one-to-one) and surjective (onto) properties, making them bijections. Their injectivity ensures that distinct inputs map to distinct outputs, preserving uniqueness and structure within mathematical systems. These functions serve as fundamental building blocks in algebra and topology, maintaining identity under composition and enabling reversible transformations.
Properties and Applications of Injective Functions
Injective functions, also known as one-to-one functions, have the property that each element of the domain maps to a unique element in the codomain, ensuring no two distinct inputs share the same output. This property guarantees invertibility on the image, making injective functions crucial in defining one-to-one correspondences and embeddings in mathematics and computer science. Applications of injective functions include cryptography for secure encoding, database indexing for unique key identification, and function inverses in calculus and abstract algebra.
Real-world Examples: Identity vs Injective Functions
Identity functions return the input value exactly as output, such as an ID card number remaining unchanged for identification purposes. Injective functions map each input to a unique output, similar to assigning distinct license plates to vehicles to avoid duplication. In databases, identity functions ensure data integrity by maintaining original entries, while injective functions guarantee unique mappings suitable for indexing records.
Common Misconceptions Between Identity and Injective
Identity functions map every element to itself, while injective functions map distinct elements to distinct images but are not limited to identity mapping. A common misconception is that all injective functions must be identity functions, which is incorrect since injectivity only requires uniqueness, not equality of input and output. Understanding that identity is a special case of injective functions clarifies their distinct but related properties in mathematics.
Identity and Injective in Set Theory
In set theory, an identity function on a set \( A \) is defined as \( \text{id}_A(x) = x \) for every element \( x \in A \), mapping each element to itself without alteration. An injective function, or one-to-one function, ensures that distinct elements in the domain correspond to distinct elements in the codomain, formally \( f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \). While every identity function is injective, not all injective functions are identity functions, since injective functions can map elements to different values while preserving uniqueness.
Importance in Abstract Algebra and Beyond
Identity and injective functions hold critical importance in abstract algebra, where the identity map preserves structure and serves as the foundation for defining automorphisms and isomorphisms. Injective functions ensure one-to-one correspondence, enabling the embedding of algebraic structures and facilitating the study of their properties without loss of information. These concepts extend beyond pure mathematics into computer science, cryptography, and functional analysis, underpinning structure-preserving transformations and data integrity.
Identity Infographic
 libterm.com
libterm.com