Solvable problems are those that can be resolved through clear methods and logical steps, making complex challenges manageable. Understanding the principles behind solvability enhances your ability to tackle issues efficiently and confidently. Discover more about how solvability impacts various fields in the rest of this article.
Table of Comparison
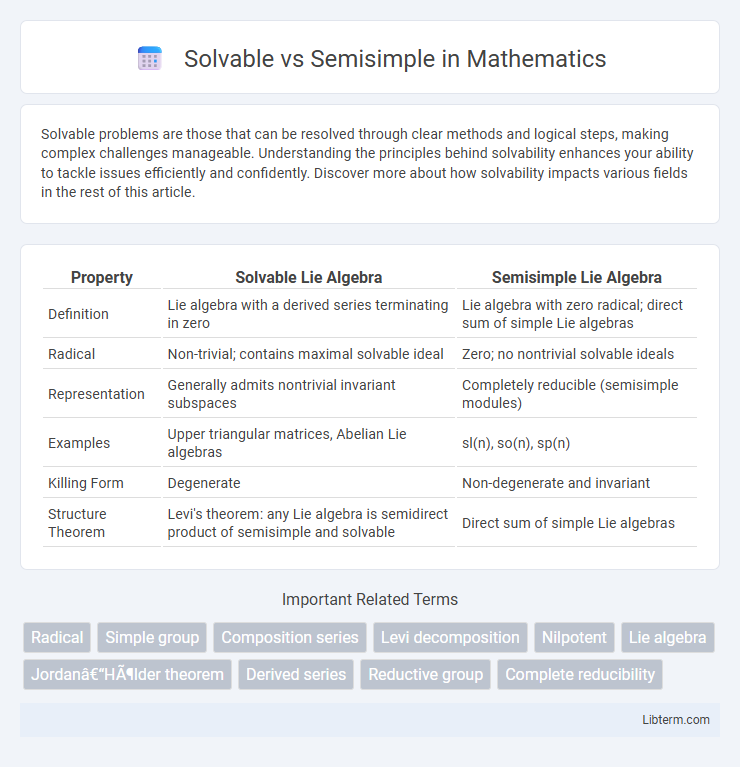
| Property | Solvable Lie Algebra | Semisimple Lie Algebra |
|---|---|---|
| Definition | Lie algebra with a derived series terminating in zero | Lie algebra with zero radical; direct sum of simple Lie algebras |
| Radical | Non-trivial; contains maximal solvable ideal | Zero; no nontrivial solvable ideals |
| Representation | Generally admits nontrivial invariant subspaces | Completely reducible (semisimple modules) |
| Examples | Upper triangular matrices, Abelian Lie algebras | sl(n), so(n), sp(n) |
| Killing Form | Degenerate | Non-degenerate and invariant |
| Structure Theorem | Levi's theorem: any Lie algebra is semidirect product of semisimple and solvable | Direct sum of simple Lie algebras |
Introduction to Solvable and Semisimple Structures
Solvable and semisimple structures frequently appear in the study of Lie algebras and algebraic groups, with solvable structures characterized by a derived series terminating in the zero algebra. Semisimple structures, in contrast, decompose into direct sums of simple algebras and lack nontrivial solvable ideals. Understanding these foundational differences is crucial for exploring representation theory and structural decomposition in modern algebra.
Defining Solvable Groups and Algebras
Solvable groups are defined by a series of subgroups where each is normal in the next, and the successive quotient groups are abelian, reflecting a stepwise simplification to commutative structures. In algebra, solvable Lie algebras possess a derived series terminating in the zero algebra, indicating a hierarchy reducible to abelian ideals. This contrasts with semisimple structures, characterized by direct sums of simple components and absence of nontrivial solvable ideals.
Understanding Semisimple Groups and Algebras
Semisimple groups and algebras are characterized by the absence of nontrivial solvable ideals, making their structure decomposable into direct sums of simple components. Unlike solvable groups, which have a series of subgroups leading to abelian quotients, semisimple groups exhibit rigidity and rich representation theory, central to Lie algebras and algebraic groups. The semisimplicity condition ensures complete reducibility of modules and the presence of invariant bilinear forms, critical in classifying finite-dimensional semisimple Lie algebras.
Key Differences: Solvable vs Semisimple
Solvable Lie algebras have a derived series terminating in the zero subalgebra, indicating a structure built from abelian layers, whereas semisimple Lie algebras decompose into a direct sum of simple Lie algebras with no nontrivial solvable ideals. Solvable algebras often appear in the study of nilpotent and triangularizable matrices, while semisimple algebras underlie the classification of complex Lie groups and exhibit fully reducible representations. The Killing form is degenerate in solvable algebras but non-degenerate in semisimple algebras, providing a key test for semisimplicity.
Historical Background and Development
Solvable and semisimple Lie algebras emerged from the foundational work of Wilhelm Killing and Elie Cartan in the late 19th and early 20th centuries, who classified complex Lie algebras through their structural properties. Solvable Lie algebras, characterized by their derived series terminating in zero, were pivotal in understanding the decomposition of Lie algebras into simpler components. The development of semisimple Lie algebras, based on Cartan's classification theorem, revolutionized representation theory and algebraic geometry by identifying algebras with no nontrivial solvable ideals and enabling the use of root system analysis.
Examples of Solvable Structures
Solvable Lie algebras include the algebra of upper triangular matrices and the Heisenberg algebra, which exhibit a derived series terminating in the zero algebra. These structures contrast with semisimple Lie algebras, such as \(\mathfrak{sl}(n, \mathbb{C})\), that have no nontrivial solvable ideals. Solvable groups like the group of affine transformations on the real line provide concrete examples of solvable Lie groups with a chain of normal subgroups having abelian quotient groups.
Examples of Semisimple Structures
Semisimple Lie algebras are characterized by their decomposition into a direct sum of simple Lie algebras, such as \(\mathfrak{sl}_n(\mathbb{C})\), \(\mathfrak{so}_n(\mathbb{R})\), and \(\mathfrak{sp}_{2n}(\mathbb{C})\), which lack non-trivial solvable ideals. In contrast, solvable Lie algebras, exemplified by the Lie algebra of upper triangular matrices, contain a chain of ideals leading to the trivial algebra. Semisimple structures play a crucial role in representation theory and algebraic groups, with their non-degenerate Killing form providing a key criterion for semisimplicity.
Applications in Mathematics and Physics
Solvable Lie algebras are extensively used in constructing integrable systems and solving differential equations in mathematical physics, where their ability to reduce complex problems into simpler substructures is crucial. Semisimple Lie algebras underpin the classification of elementary particles and gauge theories in quantum physics, providing a framework for symmetry and conservation laws through their rich representation theory. Both play vital roles in geometric approaches to theoretical physics, with solvable algebras aiding in exact solutions and semisimple algebras enabling the analysis of fundamental forces via symmetry groups.
Characteristic Properties and Theorems
Solvable Lie algebras have a derived series terminating in the zero algebra, characterized by the Engel theorem stating that all eigenvalues of the adjoint representation are zero. Semisimple Lie algebras decompose into direct sums of simple Lie algebras, featuring the Cartan criterion where the Killing form is non-degenerate. The Levi decomposition theorem asserts that any Lie algebra can be expressed as a semidirect product of its solvable radical and a semisimple subalgebra.
Summary and Future Perspectives
Solvable Lie algebras are characterized by a derived series terminating at zero and play a critical role in understanding the structure of algebraic systems through decomposition. Semisimple Lie algebras, defined by the absence of non-zero solvable ideals, exhibit complete reducibility and underpin the classification of complex Lie algebra representations. Future research aims to explore advanced applications in theoretical physics and geometry, improve computational methods for algebraic classification, and deepen the connections between solvable and semisimple structures in modern algebra.
Solvable Infographic
 libterm.com
libterm.com