A concave shape curves inward, creating a hollow or recessed surface often seen in mirrors, lenses, and reflective objects. This geometry enhances focus and magnification, influencing various applications in optics and design. Explore the article to discover how concave structures impact everyday technology and your visual experience.
Table of Comparison
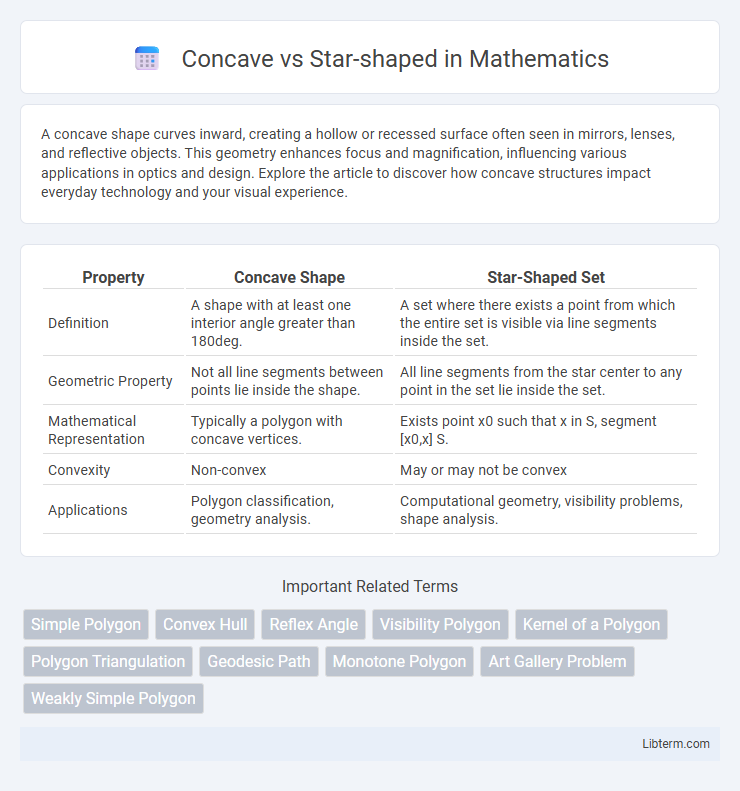
| Property | Concave Shape | Star-Shaped Set |
|---|---|---|
| Definition | A shape with at least one interior angle greater than 180deg. | A set where there exists a point from which the entire set is visible via line segments inside the set. |
| Geometric Property | Not all line segments between points lie inside the shape. | All line segments from the star center to any point in the set lie inside the set. |
| Mathematical Representation | Typically a polygon with concave vertices. | Exists point x0 such that x in S, segment [x0,x] S. |
| Convexity | Non-convex | May or may not be convex |
| Applications | Polygon classification, geometry analysis. | Computational geometry, visibility problems, shape analysis. |
Introduction to Concave and Star-Shaped Geometry
Concave geometry features shapes where at least one interior angle exceeds 180 degrees, causing the figure to have an inward indentation. Star-shaped geometry refers to domains where a point exists such that every point in the shape is visible from it, emphasizing central visibility and connectivity. These fundamental distinctions impact computational geometry, shape analysis, and collision detection algorithms.
Defining Concave Shapes: Key Characteristics
Concave shapes are defined by their inward curves or indentations, where at least one internal angle exceeds 180 degrees, distinguishing them from convex and star-shaped polygons. These key characteristics cause concave shapes to have parts of their interior "caved in," affecting properties like line visibility and polygon simplicity. Understanding concave geometry is essential for computer graphics, collision detection, and shape analysis tasks.
Understanding Star-Shaped Figures: An Overview
Star-shaped figures are defined by the existence of at least one point from which the entire shape's interior is visible, distinguishing them from concave figures that have inward indentations blocking such visibility. These shapes extend the concept of convexity by allowing certain concavities while maintaining a line of sight from a central star point to every boundary point. Star-shaped polygons play a crucial role in computational geometry and computer graphics, facilitating efficient algorithms for visibility, motion planning, and rendering tasks.
Visual Differences: Concave vs Star-Shaped
Concave shapes feature at least one interior angle greater than 180 degrees, causing parts of the shape to cave inward, creating an indentation. Star-shaped figures consist of multiple points extending outward from a central area, forming sharp protrusions and a non-convex outline. The visual distinction lies in concave shapes showing inward curves, while star-shaped polygons display prominent outward spikes or arms.
Mathematical Properties and Formulas
Concave polygons have at least one interior angle greater than 180 degrees, causing at least one vertex to point inward, while star-shaped polygons contain a point from which the entire polygon is visible, making them a subset of concave shapes. The convex hull of a concave polygon is larger than the polygon itself, and its area can be calculated using the Shoelace formula, though visibility properties require more complex ray casting methods. Star-shaped polygons satisfy the kernel property, where a kernel intersection of half-planes exists, and their star-shaped nature allows for formulas involving radial functions and kernel computation in computational geometry.
Practical Applications in Design and Architecture
Concave shapes are widely utilized in architectural design to create dynamic spaces that enhance acoustics and natural light diffusion, often seen in amphitheaters and modern building facades. Star-shaped geometries find practical applications in urban planning and landscape architecture, facilitating efficient spatial organization and aesthetic appeal through radial symmetry and multiple focal points. Both forms optimize structural integrity and visual interest, influencing functional layouts and innovative design solutions.
Advantages of Concave Shapes
Concave shapes provide enhanced structural integrity and increased surface area, which improves material strength and grip in engineering and design applications. Their inward curves allow for better energy absorption and distribution, making them ideal in impact-resistant products and ergonomic tools. These shapes also enable more efficient fluid dynamics and aerodynamics by reducing drag and promoting smoother flow patterns.
Benefits of Star-Shaped Structures
Star-shaped structures offer enhanced spatial efficiency and improved load distribution compared to concave designs, making them ideal for architectural and engineering applications. Their geometry provides greater stability and resilience under stress, optimizing material usage while maximizing functional space. These benefits contribute to sustainable construction practices and innovative design solutions.
Common Misconceptions and Clarifications
Concave polygons often face the misconception that all interior angles must be greater than 180 degrees, while star-shaped polygons are wrongly assumed to always have sharp, pointed vertices. Clarifying these, concave polygons contain at least one interior angle greater than 180 degrees but may have vertices not forming star-like points, whereas star-shaped polygons have a kernel point from which the entire polygon is visible, regardless of angle size. Understanding these distinctions aids in polygon classification in computational geometry and graphical modeling.
Conclusion: Choosing Concave or Star-Shaped
Choosing between concave and star-shaped structures depends on the specific application and desired properties such as light distribution, aesthetics, or structural integrity. Concave shapes provide better aerodynamic efficiency and smoother light diffusion, while star-shaped designs offer enhanced visual impact and stronger load-bearing capabilities. Ultimately, the decision hinges on balancing functional performance with design requirements for optimal results.
Concave Infographic
 libterm.com
libterm.com