The Hom functor is a fundamental concept in category theory and algebra that associates to each pair of objects the set of morphisms between them, encapsulating structure-preserving maps in a precise way. It plays a crucial role in defining and understanding natural transformations, adjunctions, and various homological algebra constructs. Dive into the rest of this article to explore how the Hom functor shapes modern mathematical frameworks and your understanding of abstract algebra.
Table of Comparison
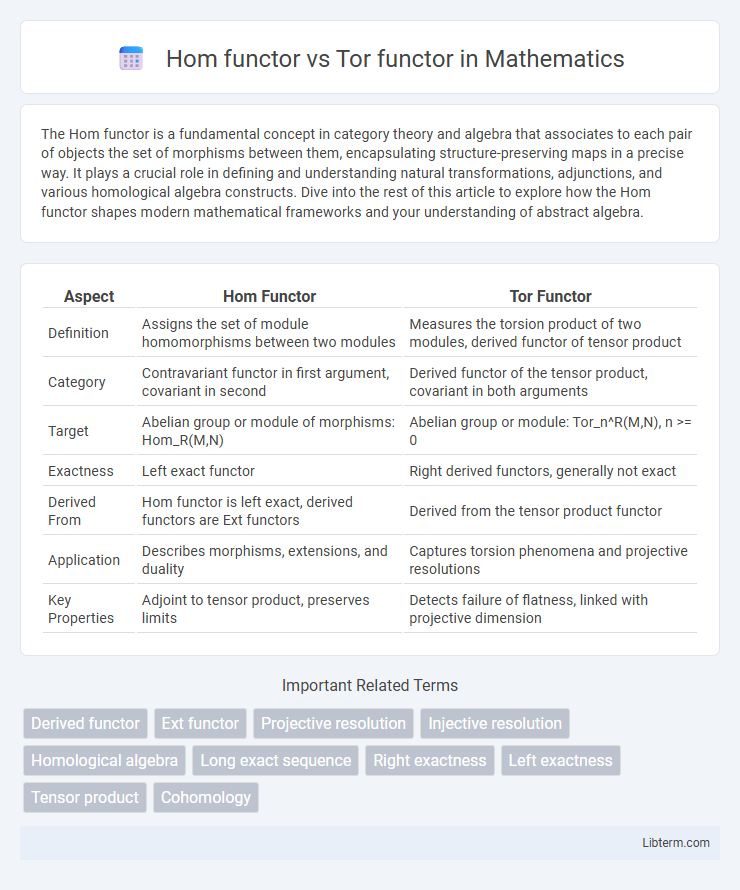
| Aspect | Hom Functor | Tor Functor |
|---|---|---|
| Definition | Assigns the set of module homomorphisms between two modules | Measures the torsion product of two modules, derived functor of tensor product |
| Category | Contravariant functor in first argument, covariant in second | Derived functor of the tensor product, covariant in both arguments |
| Target | Abelian group or module of morphisms: Hom_R(M,N) | Abelian group or module: Tor_n^R(M,N), n >= 0 |
| Exactness | Left exact functor | Right derived functors, generally not exact |
| Derived From | Hom functor is left exact, derived functors are Ext functors | Derived from the tensor product functor |
| Application | Describes morphisms, extensions, and duality | Captures torsion phenomena and projective resolutions |
| Key Properties | Adjoint to tensor product, preserves limits | Detects failure of flatness, linked with projective dimension |
Introduction to Functors in Homological Algebra
The Hom functor and Tor functor are fundamental constructions in homological algebra that measure different types of interactions between modules. The Hom functor, denoted as Hom_R(-, -), assigns to each pair of R-modules the set of R-linear homomorphisms, capturing morphisms and preserving exactness in the first variable when it is projective. The Tor functor, derived from the tensor product, reveals information about the failure of flatness of modules by computing left derived functors of the tensor product, playing a crucial role in detecting extensions and relations in module categories.
Overview of the Hom Functor
The Hom functor, denoted as Hom_R(-, M) for a module M over a ring R, assigns to each R-module N the abelian group of R-linear maps from N to M, capturing morphisms within module categories. It is a covariant functor in the second argument and contravariant in the first, playing a central role in homological algebra by linking module homomorphisms to exact sequences. Unlike the Tor functor, which measures torsion and derives from tensor products, the Hom functor encodes structure-preserving maps, facilitating the study of extensions, duality, and representability in category theory.
Overview of the Tor Functor
The Tor functor arises in homological algebra as a derived functor of the tensor product, measuring the failure of flatness of modules over a ring. It calculates the torsion created when tensoring two modules together, specifically capturing higher-dimensional "twisting" phenomena not visible via the ordinary tensor product. Tor groups, denoted by Tor_n^R(M, N), play a crucial role in computing extensions and resolving projective or flat resolutions in module theory.
Key Differences Between Hom and Tor Functors
The Hom functor, denoted as Hom_R(-, -), measures morphisms between modules and preserves exactness in the first variable when fixed, reflecting module homomorphisms and dualities. In contrast, the Tor functor, Tor^R_i(-, -), captures the derived functors of the tensor product, detecting extensions and measuring failure of flatness through projective resolutions. Hom functors are covariant in the second variable and contravariant in the first, while Tor functors are symmetric and derive from tensor products, revealing deeper homological properties of modules over a ring R.
Exactness Properties: Hom vs Tor
The Hom functor is left exact, preserving exact sequences when applied to short exact sequences, but it is not generally right exact, often requiring derived functors like Ext to measure its failure to be exact on the right. In contrast, the Tor functor is right exact, capturing the failure of tensoring to be exact on the left, and arises as a derived functor of the tensor product, reflecting how modules fail to be flat. Exactness properties distinguish Hom as a left exact contravariant functor and Tor as a right exact covariant functor, each playing complementary roles in homological algebra.
Applications of the Hom Functor
The Hom functor plays a crucial role in module theory and homological algebra, facilitating the study of morphisms between modules and enabling the construction of derived functors to analyze extensions and cohomology groups. It aids in representing internal hom-sets in categories enriched over abelian groups, which is essential in understanding duality theories and adjunctions. Applications include computing Ext groups, characterizing projective and injective modules, and providing a foundation for spectral sequences used in algebraic topology and algebraic geometry.
Applications of the Tor Functor
The Tor functor measures the degree of torsion in modules, playing a crucial role in homological algebra and algebraic topology, especially in computing derived functors of tensor products. It helps analyze projective resolutions and detects non-flatness of modules, with applications in deformation theory, sheaf cohomology, and intersection theory in algebraic geometry. Tor also provides valuable insights into extension problems and syzygies, facilitating deeper understanding of module structures and their relationships.
Computational Techniques for Hom and Tor
Computational techniques for the Hom functor often involve leveraging projective or injective resolutions to calculate morphisms between modules, utilizing Ext groups as higher derived functors to extract homological information. In contrast, Tor functor computations rely on flat or projective resolutions to determine tensor product-derived torsion modules, emphasizing the use of spectral sequences or chain complexes to resolve intricate module structures. Both functors play crucial roles in homological algebra, with efficient algorithms exploiting minimal resolutions and computer algebra systems like Macaulay2 or Singular to handle complex algebraic data and compute precise module invariants.
Examples Illustrating Hom and Tor Functors
The Hom functor, exemplified by \(\text{Hom}_{\mathbb{Z}}(\mathbb{Z}/2\mathbb{Z}, \mathbb{Z}/4\mathbb{Z}) \cong \mathbb{Z}/2\mathbb{Z}\), maps module homomorphisms and describes morphism sets, highlighting how group extensions function on hom-sets. The Tor functor, such as \(\mathrm{Tor}_1^{\mathbb{Z}}(\mathbb{Z}/2\mathbb{Z}, \mathbb{Z}/4\mathbb{Z}) \cong \mathbb{Z}/2\mathbb{Z}\), measures the failure of flatness and captures torsion phenomena in tensor products. These examples demonstrate Hom controlling module maps while Tor detects torsion obstructions in exact sequences of modules over rings like \(\mathbb{Z}\).
Hom and Tor Functors in Derived Categories
In derived categories, the Hom functor extends to the derived Hom functor, capturing morphisms between complexes with homological information encoded via Ext groups. The Tor functor arises from the left-derived tensor product, measuring the failure of flatness and providing derived invariants such as Tor groups between complexes. Both functors play fundamental roles in homological algebra, with derived Hom representing internal homs and derived Tor computing derived tensor products, essential for understanding complex interactions in triangulated categories.
Hom functor Infographic
 libterm.com
libterm.com