Matrix theory explores the properties and applications of matrices in solving complex mathematical problems, including linear transformations and systems of equations. Understanding eigenvalues, eigenvectors, and matrix decompositions is crucial for advancements in fields like computer graphics, engineering, and data science. Dive into the rest of the article to enhance your grasp of matrix theory and its practical uses.
Table of Comparison
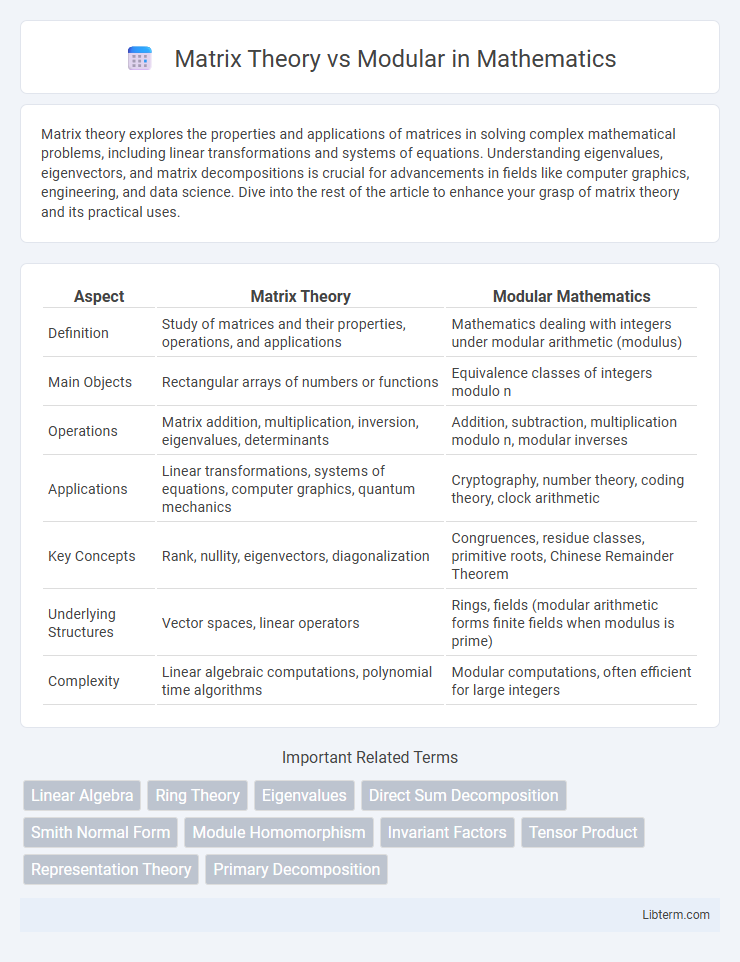
| Aspect | Matrix Theory | Modular Mathematics |
|---|---|---|
| Definition | Study of matrices and their properties, operations, and applications | Mathematics dealing with integers under modular arithmetic (modulus) |
| Main Objects | Rectangular arrays of numbers or functions | Equivalence classes of integers modulo n |
| Operations | Matrix addition, multiplication, inversion, eigenvalues, determinants | Addition, subtraction, multiplication modulo n, modular inverses |
| Applications | Linear transformations, systems of equations, computer graphics, quantum mechanics | Cryptography, number theory, coding theory, clock arithmetic |
| Key Concepts | Rank, nullity, eigenvectors, diagonalization | Congruences, residue classes, primitive roots, Chinese Remainder Theorem |
| Underlying Structures | Vector spaces, linear operators | Rings, fields (modular arithmetic forms finite fields when modulus is prime) |
| Complexity | Linear algebraic computations, polynomial time algorithms | Modular computations, often efficient for large integers |
Introduction to Matrix Theory and Modular Approach
Matrix Theory explores the study of matrices and their algebraic properties, focusing on operations such as addition, multiplication, and inversion to solve systems of linear equations and perform transformations in vector spaces. The Modular Approach divides complex linear algebra problems into smaller, manageable subproblems using modules over rings, enhancing computational efficiency and theoretical analysis. Understanding the foundational differences between conventional matrix manipulation and the modular decomposition framework is essential for advanced applications in cryptography, coding theory, and computer algebra systems.
Historical Evolution of Matrix Theory
Matrix theory originated in the mid-19th century with contributions from mathematicians like Arthur Cayley and James Joseph Sylvester, who formalized matrices as algebraic objects. The historical evolution of matrix theory was driven by applications in linear algebra, systems of equations, and later, quantum mechanics, which expanded its relevance in scientific research. Over time, matrix theory developed into a foundational discipline in both pure and applied mathematics, distinct from modular arithmetic that focuses on integer remainders and number theory.
Foundations of Modular Mathematics
Matrix theory provides a framework for representing and solving linear equations using arrays of numbers, essential in applied mathematics and engineering. Modular mathematics, rooted in number theory, studies integers with respect to a fixed modulus, forming the basis for cryptographic algorithms and coding theory. The foundations of modular mathematics emphasize congruences, residue classes, and modular arithmetic operations, which diverge from classical matrix theory by focusing on discrete cyclic structures rather than real or complex vector spaces.
Key Concepts: Matrix Operations vs Modular Arithmetic
Matrix theory centers on matrix operations such as addition, multiplication, determinant calculation, and inversion, which are essential for solving linear equations and transforming geometric data. Modular arithmetic involves computations within a finite set of integers defined by a modulus, emphasizing addition, subtraction, multiplication, and finding modular inverses under a congruence relation. The key distinction lies in matrix operations manipulating arrays of numbers to perform linear transformations, while modular arithmetic restricts calculations to a cyclical integer system, enabling applications in cryptography and computer science.
Applications in Cryptography and Computer Science
Matrix theory underpins numerous cryptographic algorithms by enabling complex linear transformations essential for encryption and decryption processes, particularly in public-key cryptosystems and error-correcting codes. Modular arithmetic serves as the foundation for many cryptographic protocols, including RSA and Diffie-Hellman, by facilitating operations within finite fields that ensure secure key generation and digital signatures. Combining matrix theoretic concepts with modular computations advances techniques in coding theory, secure multiparty computation, and post-quantum cryptography, enhancing algorithmic efficiency and security.
Strengths and Limitations of Matrix Theory
Matrix theory excels in solving linear systems, eigenvalue analysis, and transformations in various dimensions, providing a robust framework for computational efficiency and structural insights. Its strengths include straightforward application to numerical methods and clear representation of complex linear relationships, but limitations involve challenges with non-linear systems and scalability issues in extremely large or sparse matrices. Modular approaches offer flexibility in handling discrete structures and modular arithmetic, complementing matrix theory where linear assumptions do not hold.
Advantages and Challenges of Modular Methods
Modular methods in matrix theory offer advantages such as reduced computational complexity and efficient handling of large integer matrices by breaking problems into smaller, manageable modular computations. These approaches enhance numerical stability and parallelization potential, allowing faster matrix operations compared to traditional methods reliant on floating-point arithmetic. Challenges include the need for careful system reconstruction from modular results and managing issues related to modulus selection to avoid information loss or increased overhead in the Chinese remainder theorem application.
Comparative Analysis: Performance and Efficiency
Matrix theory excels in solving linear algebra problems with high accuracy, making it ideal for large-scale scientific computations where precise numerical solutions are required. Modular arithmetic algorithms offer superior computational efficiency in cryptographic applications by reducing complexity and enhancing speed through operations within finite fields. Performance comparisons reveal matrix methods are computationally intensive but versatile, whereas modular techniques provide faster execution and lower memory usage in discrete systems, highlighting the preference for modular approaches in real-time and resource-constrained environments.
Real-World Use Cases in Engineering and Data Science
Matrix theory underpins structural analysis in civil engineering, enabling the modeling of stress and strain in materials through systems of linear equations. Modular arithmetic is crucial in cryptography and error detection algorithms prevalent in secure communications and data integrity verification within data science. Real-world applications leverage matrix decompositions for machine learning algorithms, while modular systems optimize computational efficiency in hashing and blockchain technology.
Future Perspectives: Integrating Matrix and Modular Techniques
Integrating matrix theory and modular techniques promises enhanced computational efficiency and scalability in solving complex algebraic systems, particularly in cryptography and coding theory. Advances in algorithmic frameworks that leverage both matrix decompositions and modular arithmetic are expected to optimize data encryption processes and error correction methods. Future research aims to develop hybrid models that exploit structural matrix properties alongside modular constraints for improved performance in technical computing and secure communications.
Matrix Theory Infographic
 libterm.com
libterm.com