The homeomorphism group of a topological space consists of all continuous bijections with continuous inverses, preserving the space's structure under deformation. This group plays a crucial role in understanding the space's symmetries and topological invariants, impacting various fields such as geometry and dynamical systems. Explore the rest of the article to uncover deeper insights into the properties and applications of homeomorphism groups.
Table of Comparison
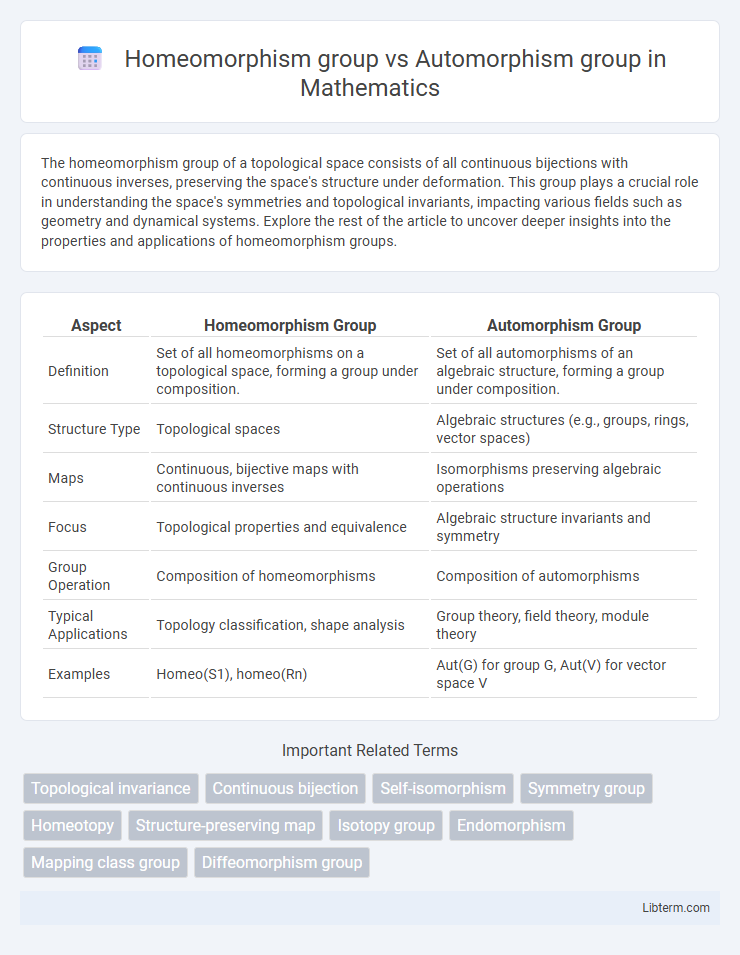
| Aspect | Homeomorphism Group | Automorphism Group |
|---|---|---|
| Definition | Set of all homeomorphisms on a topological space, forming a group under composition. | Set of all automorphisms of an algebraic structure, forming a group under composition. |
| Structure Type | Topological spaces | Algebraic structures (e.g., groups, rings, vector spaces) |
| Maps | Continuous, bijective maps with continuous inverses | Isomorphisms preserving algebraic operations |
| Focus | Topological properties and equivalence | Algebraic structure invariants and symmetry |
| Group Operation | Composition of homeomorphisms | Composition of automorphisms |
| Typical Applications | Topology classification, shape analysis | Group theory, field theory, module theory |
| Examples | Homeo(S1), homeo(Rn) | Aut(G) for group G, Aut(V) for vector space V |
Introduction to Topological and Algebraic Groups
The homeomorphism group of a topological space consists of all bijective continuous maps with continuous inverses, preserving the space's topological structure under composition. In contrast, the automorphism group of an algebraic structure, such as a group or ring, comprises all bijective homomorphisms preserving the algebraic operations. Studying these groups within topological and algebraic contexts reveals how symmetry and structure intertwine through continuous and algebraic transformations.
Understanding Homeomorphism Groups
Homeomorphism groups consist of all bijective continuous functions from a topological space onto itself with continuous inverses, capturing the notion of topological equivalence. These groups reflect the intrinsic geometric structure of spaces, preserving topological properties such as connectedness and compactness without necessarily preserving algebraic structures. Studying homeomorphism groups reveals fundamental insights into space classification, deformation, and topological invariants, differentiating them from automorphism groups that maintain algebraic operations in structures like groups, rings, or fields.
Exploring Automorphism Groups
Automorphism groups consist of all isomorphisms from a mathematical object to itself, preserving the object's structure, making them crucial in algebra, graph theory, and topology for understanding symmetries and invariants. Homeomorphism groups include all continuous bijections with continuous inverses on a topological space, highlighting the space's topological properties rather than algebraic structures. Exploring automorphism groups on algebraic objects like groups, rings, or graphs offers insights into the object's internal symmetries, rigidities, and classification, often facilitating algebraic and combinatorial invariant analysis.
Key Differences Between Homeomorphism and Automorphism Groups
Homeomorphism groups consist of all bijective continuous functions with continuous inverses between topological spaces, preserving topological properties, while automorphism groups encompass all isomorphisms of algebraic structures, preserving algebraic operations. The key difference lies in the nature of preservation: homeomorphisms maintain topological invariants such as connectedness and compactness, whereas automorphisms preserve algebraic structure, like group operations or ring multiplication. Homeomorphism groups act on topological spaces, making them central in topology, whereas automorphism groups operate within algebraic contexts, governing symmetries of groups, rings, fields, or vector spaces.
Structural Properties Compared
The homeomorphism group consists of all continuous bijections with continuous inverses on a topological space, emphasizing topological invariance and deformation without tearing or gluing. The automorphism group generally refers to structure-preserving bijections within algebraic structures, such as groups, rings, or vector spaces, highlighting rigid symmetry that maintains algebraic operations. Structurally, the homeomorphism group captures geometric deformations, often forming infinite-dimensional topological groups, while automorphism groups typically act as discrete or finite groups preserving exact algebraic relations.
Group Actions and Symmetries
The homeomorphism group of a topological space consists of all bijective continuous maps with continuous inverses, capturing topological symmetries through group actions that preserve the space's topology. In contrast, the automorphism group often refers to symmetries preserving additional structure, such as algebraic or geometric operations, acting on objects like groups, graphs, or vector spaces. Both groups encode symmetries via group actions, but homeomorphisms emphasize flexible, global topological invariants, while automorphisms emphasize rigid structural transformations preserving algebraic or combinatorial properties.
Examples in Topology and Algebra
The homeomorphism group consists of all bijective continuous maps with continuous inverses on a topological space, exemplified by the homeomorphism group of the circle \( S^1 \), which includes rotations and reflections preserving topological structure. The automorphism group applies to algebraic structures, such as the automorphism group of a group \( G \), capturing all isomorphisms from \( G \) to itself preserving group operations. In topology, homeomorphisms classify spaces up to topological equivalence, while in algebra, automorphisms reveal symmetries of algebraic objects like fields or vector spaces, illustrated by the automorphism group of the field \(\mathbb{C}\) fixing \(\mathbb{R}\).
Applications in Mathematics
The homeomorphism group, consisting of all continuous bijections with continuous inverses on a topological space, is pivotal in topology and geometric group theory for classifying spaces up to continuous deformation. The automorphism group, defined as all bijective structure-preserving maps on algebraic structures like groups or graphs, plays a crucial role in abstract algebra and combinatorics by revealing symmetries and invariants of these structures. Applications in mathematics leverage homeomorphism groups to study manifolds' topological classification, while automorphism groups facilitate understanding algebraic object symmetries, aiding in fields such as Galois theory and network theory.
Recent Research and Developments
Recent research in topology and algebra emphasizes distinct roles of homeomorphism and automorphism groups in understanding space symmetries and structure-preserving transformations. Advances include deepening insights into homeomorphism groups as topological groups acting on manifolds, with applications in geometric group theory and dynamical systems, while automorphism groups are explored extensively in algebraic geometry and category theory, particularly for classifying algebraic varieties and complex structures. Cutting-edge studies leverage computational techniques and homotopy-theoretic methods to analyze deformation and rigidity properties within these groups, reflecting their fundamental differences and interrelations.
Conclusion: Homeomorphism vs Automorphism Groups
Homeomorphism groups consist of all bicontinuous functions mapping a topological space onto itself, preserving its topological structure, while automorphism groups specifically refer to structure-preserving isomorphisms within algebraic or geometric contexts, such as groups, rings, or graphs. The key distinction lies in the nature of structures preserved: homeomorphisms guarantee topological equivalence, whereas automorphisms enforce rigid algebraic or combinatorial symmetry. In summary, homeomorphism groups capture global topological features, whereas automorphism groups encode intrinsic algebraic or combinatorial invariants, reflecting different layers of structural symmetry.
Homeomorphism group Infographic
 libterm.com
libterm.com