Regular continuity ensures that small changes in the input produce small changes in the output, maintaining predictability in mathematical functions. This property is crucial for analyzing limits, behavior of functions, and solving calculus problems effectively. Explore the rest of the article to deepen your understanding of regular continuity and its applications.
Table of Comparison
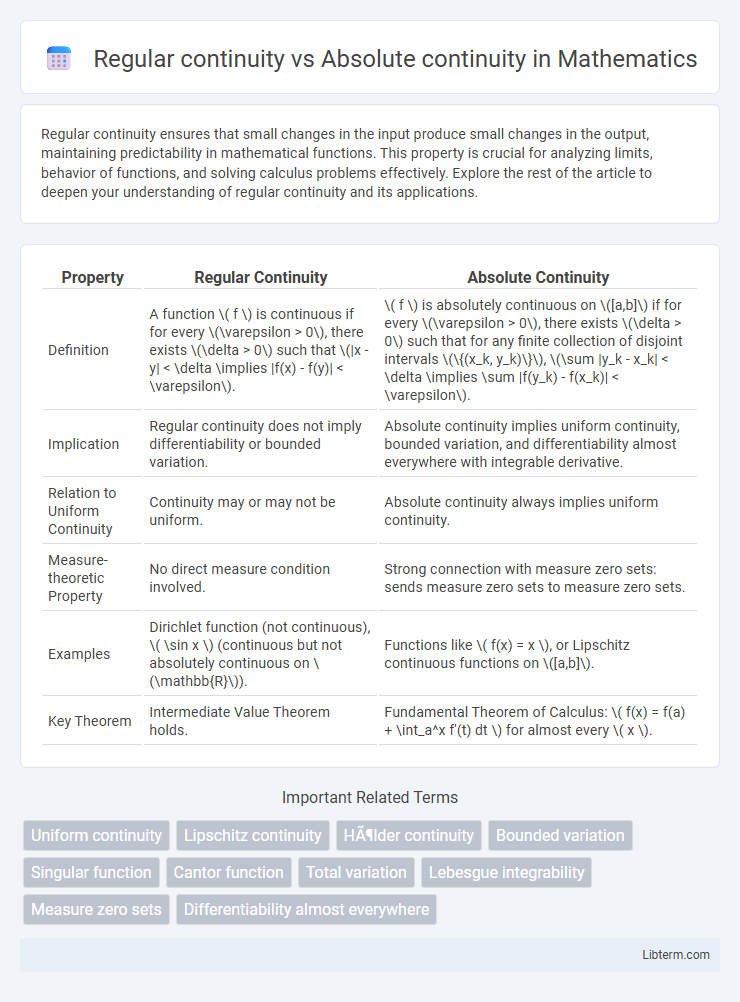
| Property | Regular Continuity | Absolute Continuity |
|---|---|---|
| Definition | A function \( f \) is continuous if for every \(\varepsilon > 0\), there exists \(\delta > 0\) such that \(|x - y| < \delta \implies |f(x) - f(y)| < \varepsilon\). | \( f \) is absolutely continuous on \([a,b]\) if for every \(\varepsilon > 0\), there exists \(\delta > 0\) such that for any finite collection of disjoint intervals \(\{(x_k, y_k)\}\), \(\sum |y_k - x_k| < \delta \implies \sum |f(y_k) - f(x_k)| < \varepsilon\). |
| Implication | Regular continuity does not imply differentiability or bounded variation. | Absolute continuity implies uniform continuity, bounded variation, and differentiability almost everywhere with integrable derivative. |
| Relation to Uniform Continuity | Continuity may or may not be uniform. | Absolute continuity always implies uniform continuity. |
| Measure-theoretic Property | No direct measure condition involved. | Strong connection with measure zero sets: sends measure zero sets to measure zero sets. |
| Examples | Dirichlet function (not continuous), \( \sin x \) (continuous but not absolutely continuous on \(\mathbb{R}\)). | Functions like \( f(x) = x \), or Lipschitz continuous functions on \([a,b]\). |
| Key Theorem | Intermediate Value Theorem holds. | Fundamental Theorem of Calculus: \( f(x) = f(a) + \int_a^x f'(t) dt \) for almost every \( x \). |
Introduction to Continuity in Mathematics
Regular continuity in mathematics refers to a function where small changes in the input produce small changes in the output, ensuring the function has no abrupt jumps. Absolute continuity extends this concept by requiring that for every small positive number, there exists a corresponding delta such that the total variation of the function over any collection of intervals with combined length less than delta is also small. This distinction is critical in real analysis, as absolute continuity implies differentiability almost everywhere and integrates directly with Lebesgue integration theory, unlike regular continuity.
Defining Regular Continuity
Regular continuity of a function at a point means the limit of the function as the input approaches that point equals the function value, ensuring no sudden jumps or breaks. This classical notion relies on the epsilon-delta definition, guaranteeing for every epsilon greater than zero, there exists a delta such that the function's values remain within epsilon whenever the input is within delta of the point. Regular continuity contrasts with absolute continuity, where the latter additionally requires the function to map sets of small measure to sets of small measure, implying stronger integrability and differentiability properties.
Understanding Absolute Continuity
Absolute continuity of a function ensures that for every e > 0, there exists a d > 0 such that whenever a finite collection of non-overlapping intervals sum to less than d in length, the sum of the corresponding function value differences is less than e. This property implies uniform continuity and preserves measure-zero sets, distinguishing it from regular continuity, which only requires pointwise limit behavior. Absolute continuity is fundamental in real analysis and measure theory, particularly in characterizing functions with integrable derivatives and enabling the application of the Fundamental Theorem of Calculus for Lebesgue integrals.
Key Differences Between Regular and Absolute Continuity
Regular continuity requires that for every e > 0, there exists a d > 0 so that changes in the input less than d produce output changes less than e, focusing on pointwise behavior of functions. Absolute continuity strengthens this by demanding that for every e > 0, there exists a d > 0 such that for any collection of non-overlapping intervals with total length less than d, the sum of the function's oscillations on these intervals is less than e, ensuring preservation of measures and integrability properties. Unlike regular continuity, absolute continuity implies uniform continuity and the function has a derivative almost everywhere with its integral recovering the original function.
Mathematical Formalism of Regular Continuity
Regular continuity of a function \( f: \mathbb{R} \to \mathbb{R} \) is defined by the formal \(\epsilon\)-\(\delta\) criterion: for every \(\epsilon > 0\), there exists \(\delta > 0\) such that for all \(x, y \in \mathbb{R}\), if \(|x - y| < \delta\), then \(|f(x) - f(y)| < \epsilon\). This property ensures that small changes in the input produce arbitrarily small changes in the output, guaranteeing pointwise continuity across the domain. In contrast, absolute continuity involves stronger conditions related to measure theory, requiring the function to map sets of arbitrarily small measure to sets of small image measure, linked closely to the function's differentiability almost everywhere and integrability of its derivative.
Formal Definition and Properties of Absolute Continuity
Absolute continuity of a function \( f:[a,b] \to \mathbb{R} \) is formally defined by the condition that for every \( \epsilon > 0 \), there exists a \( \delta > 0 \) such that for any finite collection of non-overlapping intervals \(\{(x_k,y_k)\}\) within \([a,b]\), the sum \(\sum |y_k - x_k| < \delta\) implies \(\sum |f(y_k) - f(x_k)| < \epsilon\). Unlike regular continuity, absolute continuity guarantees that \( f \) can be expressed as the integral of its derivative \( f' \) almost everywhere, satisfying the fundamental theorem of calculus in the Lebesgue sense. Key properties include uniform continuity, bounded variation, differentiability almost everywhere, and preservation of measure-zero sets under \( f \).
Examples Illustrating Regular Continuity
Regular continuity is exemplified by functions like f(x) = x2, where small changes in x produce small changes in f(x), ensuring no sudden jumps. For instance, the function f(x) = sin(x) is continuous everywhere because for any e > 0, there exists d > 0 such that |x - c| < d implies |sin(x) - sin(c)| < e. Such examples contrast with absolute continuity where functions must satisfy stronger integration conditions, ensuring not only continuity but also the preservation of measure under the function.
Examples Demonstrating Absolute Continuity
Absolute continuity of a function f on [a,b] implies that for every e > 0, there exists d > 0 such that for any finite collection of non-overlapping intervals {(x_k, y_k)} in [a,b] with total length less than d, the sum of |f(y_k) - f(x_k)| is less than e. An example is the Cantor-Lebesgue function, which is continuous but not absolutely continuous, whereas the function f(x) = x2 on [0,1] is absolutely continuous because it can be expressed as an integral of its derivative f'(x) = 2x, satisfying the fundamental theorem of calculus. Functions of bounded variation that are singular, like the Cantor function, highlight the necessity of absolute continuity for representing a function as the integral of its derivative, differentiating it from mere regular continuity.
Implications in Analysis and Real-World Applications
Regular continuity ensures that small changes in input produce small changes in output, which is fundamental in calculus and real analysis for defining limits and derivatives. Absolute continuity is a stronger condition that guarantees the function can be represented as an integral of its derivative, facilitating advanced integration techniques, measure theory, and the Fundamental Theorem of Calculus. In real-world applications, absolute continuity allows precise modeling of phenomena like fluid flow, material deformation, and financial asset pricing by ensuring both smooth behavior and integrability under varying conditions.
Summary: Choosing Between Regular and Absolute Continuity
Regular continuity ensures a function maintains closeness of outputs for close inputs, suitable for general analysis and modeling. Absolute continuity strengthens this by guaranteeing the function's variation is controlled by the measure of intervals, critical in advanced integration, measure theory, and differentiability contexts. Selecting between regular and absolute continuity depends on application needs: absolute continuity is essential for precise integral representation and differentiability, while regular continuity suffices for most basic continuity requirements.
Regular continuity Infographic
 libterm.com
libterm.com