The universal enveloping algebra is a fundamental construction in Lie algebra theory, providing an associative algebra that contains a given Lie algebra as a subalgebra. It plays a crucial role in representation theory by allowing Lie algebra elements to act on modules in a well-defined manner. Discover how the universal enveloping algebra bridges abstract algebraic concepts and practical applications in the full article.
Table of Comparison
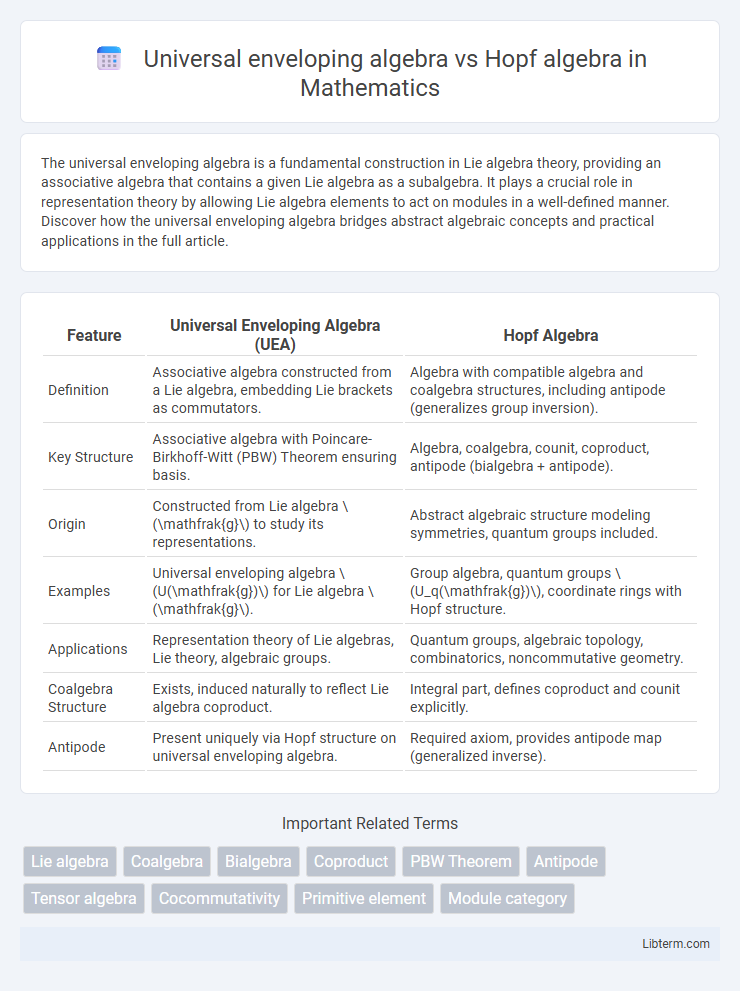
| Feature | Universal Enveloping Algebra (UEA) | Hopf Algebra |
|---|---|---|
| Definition | Associative algebra constructed from a Lie algebra, embedding Lie brackets as commutators. | Algebra with compatible algebra and coalgebra structures, including antipode (generalizes group inversion). |
| Key Structure | Associative algebra with Poincare-Birkhoff-Witt (PBW) Theorem ensuring basis. | Algebra, coalgebra, counit, coproduct, antipode (bialgebra + antipode). |
| Origin | Constructed from Lie algebra \(\mathfrak{g}\) to study its representations. | Abstract algebraic structure modeling symmetries, quantum groups included. |
| Examples | Universal enveloping algebra \(U(\mathfrak{g})\) for Lie algebra \(\mathfrak{g}\). | Group algebra, quantum groups \(U_q(\mathfrak{g})\), coordinate rings with Hopf structure. |
| Applications | Representation theory of Lie algebras, Lie theory, algebraic groups. | Quantum groups, algebraic topology, combinatorics, noncommutative geometry. |
| Coalgebra Structure | Exists, induced naturally to reflect Lie algebra coproduct. | Integral part, defines coproduct and counit explicitly. |
| Antipode | Present uniquely via Hopf structure on universal enveloping algebra. | Required axiom, provides antipode map (generalized inverse). |
Introduction to Universal Enveloping Algebras
Universal enveloping algebras provide an associative algebra construction that encodes the Lie algebra structure, allowing representation theory techniques to be applied. They serve as a cornerstone in the study of Hopf algebras by offering an explicit example where the algebraic and coalgebraic structures coexist, facilitating coalgebraic operations like coproducts and antipodes. The universal property ensures every Lie algebra homomorphism to an associative algebra extends uniquely to a map from its universal enveloping algebra, underpinning their fundamental role in quantum group theory and deformation theory.
Overview of Hopf Algebras
Hopf algebras are algebraic structures that simultaneously carry compatible algebra and coalgebra structures, along with an antipode map enabling the definition of an inverse under convolution. They generalize group algebras and universal enveloping algebras of Lie algebras, providing a framework for symmetry in quantum groups and noncommutative geometry. The interplay between multiplication, comultiplication, unit, counit, and antipode maps defines the coherence axioms essential to the Hopf algebra structure.
Historical Development and Motivation
The universal enveloping algebra emerged in the early 20th century as a means to bridge Lie algebras with associative algebras, enabling the representation theory of Lie groups through algebraic structures. Hopf algebras were introduced later in the mid-20th century to generalize group symmetries in algebraic topology and quantum groups, formalizing concepts of algebraic operations, co-operations, and antipodes. The development of Hopf algebras extended the scope of universal enveloping algebras by providing a framework for duality and deformation theory in non-commutative geometry.
Core Definitions and Structures
Universal enveloping algebras arise from Lie algebras, providing an associative algebra that contains the Lie algebra as a Lie subalgebra via the commutator bracket, constructed through the tensor algebra modulo the ideal generated by relations defining the Lie bracket. Hopf algebras generalize universal enveloping algebras by equipping associative algebras with a coalgebra structure, including comultiplication, counit, and antipode maps that satisfy compatibility axioms, enabling duality and symmetry operations in algebraic structures. The universal enveloping algebra of a Lie algebra naturally inherits a Hopf algebra structure, where the comultiplication encodes the Lie bracket's cocommutative properties and facilitates representation theory through module categories.
Universal Enveloping Algebra: Properties and Examples
Universal enveloping algebra (UEA) of a Lie algebra encapsulates its structure in an associative algebra, preserving the Lie bracket via commutators. Key properties include the Poincare-Birkhoff-Witt theorem, ensuring a basis correspondence between the Lie algebra and its UEA, and the existence of a natural Hopf algebra structure on the UEA with comultiplication, counit, and antipode. Examples of universal enveloping algebras appear in the study of semisimple Lie algebras like \(\mathfrak{sl}_2(\mathbb{C})\), where representation theory and module categorizations heavily rely on UEA constructions.
Hopf Algebra: Properties and Examples
Hopf algebras are algebraic structures equipped with operations of multiplication, comultiplication, antipode, unit, and counit, enabling a rich interplay between algebra and coalgebra. They provide a framework for studying symmetry in algebraic topology, quantum groups, and noncommutative geometry, with core examples including group algebras, universal enveloping algebras of Lie algebras, and coordinate rings of algebraic groups. Key properties such as the antipode's role as a convolution inverse and the compatibility between multiplication and comultiplication distinguish Hopf algebras from universal enveloping algebras, which primarily focus on associative algebra representations of Lie algebras.
Structural Similarities and Differences
Universal enveloping algebras are associative algebras constructed from Lie algebras, embedding the Lie bracket into an algebraic framework, whereas Hopf algebras combine algebraic and coalgebraic structures with antipode maps, enabling dual operations like multiplication and comultiplication. Structurally, both have an algebra structure with unit and multiplication, but Hopf algebras include coproduct, counit, and antipode satisfying compatibility axioms, which universal enveloping algebras acquire naturally when endowed with a suitable coalgebra structure. The key difference lies in the additional coalgebraic and antipode structures defining Hopf algebras, giving them richer symmetry and duality properties not inherently present in universal enveloping algebras without this extension.
Representation Theory in Both Algebras
The Universal Enveloping Algebra of a Lie algebra encapsulates all its representations by providing an associative algebra framework, enabling modules over it to correspond directly to Lie algebra representations. Hopf algebras extend this structure by incorporating coproducts, counits, and antipodes, facilitating the study of tensor products and duals of representations in a braided monoidal category. In representation theory, Universal Enveloping Algebras serve as a foundational tool for linearizing Lie algebra actions, whereas Hopf algebras generalize symmetry concepts beyond Lie algebras, significantly enriching module categories and intertwining operators.
Applications in Mathematics and Physics
Universal enveloping algebras provide a bridge between Lie algebras and associative algebras, playing a crucial role in representation theory and quantum mechanics, where they facilitate the study of symmetry and conserved quantities. Hopf algebras extend this structure with coproducts, antipodes, and counits, enabling the modeling of quantum groups, which are essential in noncommutative geometry and topological quantum field theory. Applications in physics include the formulation of exactly solvable models, deformation quantization, and the algebraic underpinning of particle interactions within gauge theories.
Comparative Analysis: Universal Enveloping vs Hopf Algebras
Universal enveloping algebras serve as associative algebra completions of Lie algebras, encapsulating their structure while preserving representation theory, whereas Hopf algebras enhance algebraic frameworks with coalgebraic structures, enabling concepts like antipodes and comultiplication. The key difference lies in universality and co-structures: universal enveloping algebras focus on enveloping Lie algebra actions, while Hopf algebras unify algebraic and coalgebraic properties essential in quantum groups and symmetry. Comparative analysis reveals universal enveloping algebras often instantiate Hopf algebras when endowed with natural coalgebra maps, highlighting their foundational role in algebraic topology and quantum algebra.
Universal enveloping algebra Infographic
 libterm.com
libterm.com