A free module is a module that has a basis, meaning every element can be uniquely expressed as a linear combination of basis elements with coefficients from the ring. A cyclic module, on the other hand, is generated by a single element, so every element of the module is a scalar multiple of that generator. Explore the rest of the article to understand the distinctions and applications of free and cyclic modules in greater detail.
Table of Comparison
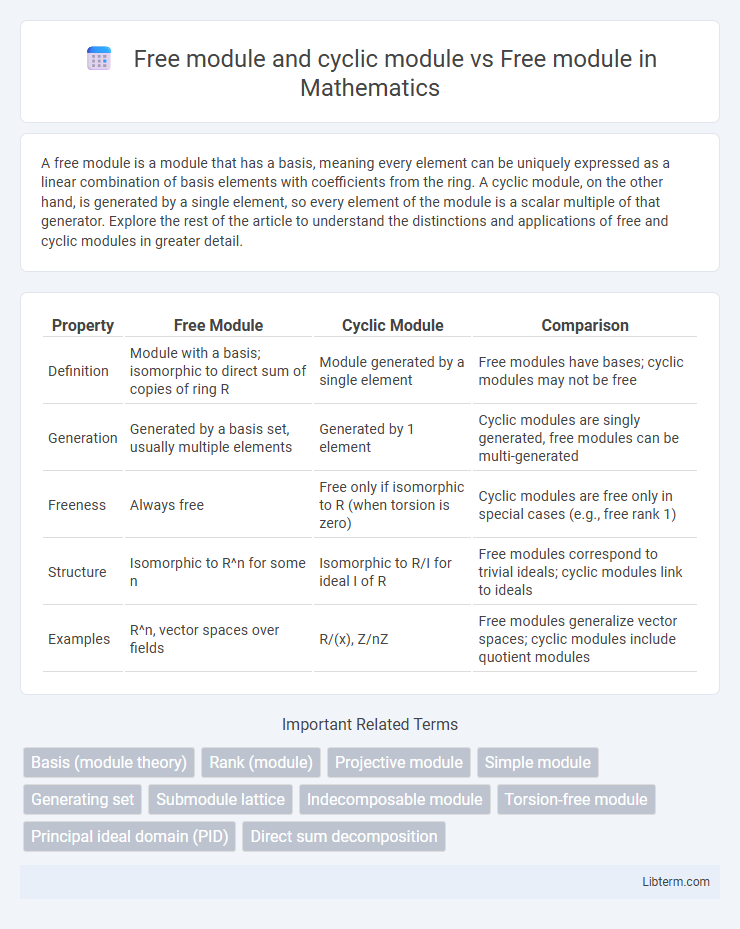
| Property | Free Module | Cyclic Module | Comparison |
|---|---|---|---|
| Definition | Module with a basis; isomorphic to direct sum of copies of ring R | Module generated by a single element | Free modules have bases; cyclic modules may not be free |
| Generation | Generated by a basis set, usually multiple elements | Generated by 1 element | Cyclic modules are singly generated, free modules can be multi-generated |
| Freeness | Always free | Free only if isomorphic to R (when torsion is zero) | Cyclic modules are free only in special cases (e.g., free rank 1) |
| Structure | Isomorphic to R^n for some n | Isomorphic to R/I for ideal I of R | Free modules correspond to trivial ideals; cyclic modules link to ideals |
| Examples | R^n, vector spaces over fields | R/(x), Z/nZ | Free modules generalize vector spaces; cyclic modules include quotient modules |
Introduction to Modules in Algebra
A free module over a ring R is a module with a basis, allowing every element to be uniquely expressed as a finite linear combination of basis elements, analogous to vector spaces over fields. Cyclic modules are generated by a single element and represent the simplest form of modules but need not be free unless the module is isomorphic to R itself as a free module of rank one. Understanding free and cyclic modules is crucial in module theory as they provide foundational examples distinguishing between more complex module structures and free modules' richer algebraic properties.
Defining Free Modules: Key Concepts
Free modules are algebraic structures characterized by having a basis, allowing every element to be uniquely expressed as a linear combination of basis elements over a ring. Cyclic modules are generated by a single element but may lack a basis that freely generates the module, distinguishing them from free modules which require linear independence of generators. Understanding these differences is fundamental in module theory, as free modules exhibit properties akin to vector spaces while cyclic modules may have torsion elements impacting their structure.
Understanding Cyclic Modules
A cyclic module is a module generated by a single element, meaning every element of the module can be expressed as a module action on that generator. Free modules, on the other hand, are direct sums of copies of the underlying ring, with a basis that allows unique representation of elements as linear combinations of basis elements. Understanding cyclic modules is crucial because they represent the simplest nontrivial modules and serve as building blocks for more complex structures, while free modules provide a framework for modules with a well-defined basis and linear independence.
Free Modules vs Cyclic Modules: Core Differences
Free modules are direct sums of copies of the underlying ring, characterized by having a basis that freely generates the module without relations. Cyclic modules are generated by a single element, making them simple but not necessarily free unless the underlying ring is a division ring. The core difference lies in the structure: free modules require a basis and can have multiple generators, while cyclic modules are inherently single-generated and may have torsion elements absent in free modules.
Structural Properties of Free Modules
Free modules possess a basis allowing every element to be uniquely expressed as a linear combination of basis elements, granting them projective and flat properties. Cyclic modules, generated by a single element, may lack this structure unless they are free of rank one over a principal ideal domain. The structural properties of free modules ensure exactness in sequences and enable straightforward homomorphism classification, contrasting with the often more constrained nature of cyclic modules.
Generation and Basis: Free vs Cyclic Modules
Free modules possess a basis consisting of linearly independent generators that span the entire module, allowing unique representation of elements as linear combinations of basis vectors. Cyclic modules are generated by a single element but may lack a basis if the module is not free, leading to potential relations among multiples of the generator. The main distinction lies in free modules having a basis with no relations among generators, whereas cyclic modules rely on a single generator possibly subject to torsion or annihilation relations.
Examples of Free Modules
A free module over a ring R is characterized by having a basis, such as R^n, the direct sum of n copies of R, which allows every element to be uniquely expressed as a linear combination of basis elements. In contrast, a cyclic module is generated by a single element, for example R/(a), the quotient of R by the ideal generated by a, which may not have a free basis if the ideal is nontrivial. Typical examples of free modules include vector spaces over a field, Z-modules like Z^n over the integers, while cyclic modules include structures like Z/nZ, showcasing the difference between free and cyclic modules through their generation and basis properties.
Examples of Cyclic Modules
A cyclic module is generated by a single element, such as \(\mathbb{Z}/n\mathbb{Z}\) over \(\mathbb{Z}\), where every element is a multiple of the generator. In contrast, a free module, like \(\mathbb{Z}^n\), has a basis consisting of multiple generators with no relations, making it isomorphic to a direct sum of copies of the ring. Examples of cyclic modules include simple modules like \(\mathbb{Z}/p\mathbb{Z}\) for prime \(p\), illustrating modules generated by one element with torsion, unlike free modules which are torsion-free.
Applications in Algebra: Free and Cyclic Modules
Free modules serve as fundamental building blocks in module theory, characterized by their basis that allows every element to be uniquely expressed as a linear combination of basis elements, facilitating straightforward algebraic computations and direct sum decompositions. Cyclic modules, generated by a single element, offer a simpler structure ideal for understanding module homomorphisms and analyzing torsion properties, particularly in the context of principal ideal domains. Applications in algebra leverage free modules for constructing projective modules and resolving modules via exact sequences, while cyclic modules simplify classification problems and provide insight into the structure of modules over rings, enhancing conceptual clarity in module theory.
Summary: Free Module vs Cyclic Module
A free module is a module with a basis, allowing every element to be uniquely expressed as a finite linear combination of basis elements, making it isomorphic to a direct sum of copies of the ring. A cyclic module is generated by a single element, often represented as the quotient of the ring by a submodule, but unlike free modules, it may have relations that prevent a basis from existing. Free modules always have a well-defined rank (the cardinality of the basis), whereas cyclic modules may lack such a basis structure, highlighting the key structural difference between free and cyclic modules.
Free module and cyclic module Infographic
 libterm.com
libterm.com